Презентация "Машинная эволюция" по информатике – проект, доклад

Глава 6. Машинная эволюция

Метод перебора, как наиболее универсальный метод поиска решений. Методы ускорения перебора. Метод группового учета аргументов как представитель эволюционных методов. Генетический алгоритм.

Автоматический синтез технических решений. Поиск оптимальных структур. Алгоритм поиска глобального экстремума. Алгоритм конкурирующих точек. Алгоритм случайного поиска в подпространствах. Некоторые замечания относительно использования ГА. Автоматизированный синтез физических принципов действия. Фонд физико-технических эффектов. Синтез физических принципов действия по заданной физической операции. Заключительные замечания (слабосвязанный мир).

Метод перебора, как наиболее универсальный метод поиска решений. Методы ускорения перебора.

Как известно, существуют задачи, для которых доказано отсутствие общего алгоритма решения (например, задача о разрешимости Диофантова множества). В то же время, можно сказать, что, если бы мы обладали бесконечным запасом времени и соответствующими ресурсами, то мы могли бы найти решение любой задачи. Здесь имеется в виду не конструирование нового знания на основании имеющегося (вывод новых теорем из аксиом и уже выведенных теорем), а, прежде всего, перебор вариантов.

Еще в XVII столетии Лейбниц пытался раскрыть тайну "Всеобщего Искусства Изобретения". Он утверждал, что одной из двух частей этого искусства является комбинаторика - перебор постепенно усложняющихся комбинаций исходных данных. Второй частью является эвристика - свойство догадки человека. И сейчас вторая часть Искусства Изобретения все еще остается нераскрытой. На языке нашего времени эта часть - модель мышления человека, включающая в себя процессы генерации эвристик (догадок, изобретений, открытий). Однако прежде чем перейти к рассмотрению улучшенных переборных алгоритмов (улучшенных потому, что для простого перебора у нас в запасе нет вечности), я бы отметил еще один универсальный метод ускорения перебора - быстрое отсечение ложных (или вероятно ложных, что и используется большинством алгоритмов) ветвей перебора.

Эволюция

Основные принципы эволюционной теории заложил Чарльз Дарвин в своей самой революционной работе - "Происхождение видов". Самым важным его выводом был вывод об основной направляющей силе эволюции - ею признавался естественный отбор. Другими словами - выживает сильнейший (в широком смысле этого слова). Забегая вперед, замечу, что любой эволюционный алгоритм имеет такой шаг, как выделение самых сильных (полезных) особей. Вторым, не менее важным выводом Дарвина был вывод об изменчивости организмов. Аналогом данного закона у всех алгоритмов является шаг генерации новых экземпляров искомых объектов (решений, структур, особей, алгоритмов).

Именно отбор наилучших объектов является ключевой эвристикой всех эволюционных методов, позволяющих зачастую уменьшить время поиска решения на несколько порядков по сравнению со случайным поиском. Если попытаться выразить эту эвристику на естественном языке, то получим: сложно получить самое лучшее решение, модифицируя плохое. Скорее всего, оно получится из нескольких лучших на данный момент. Из основных особенностей эволюционных алгоритмов можно отметить их некоторую сложность в плане настройки основных параметров (вырождение, либо неустойчивость решения). Данный недостаток следует из основной эвристики - можно "уничтожить" предка самого лучшего решения, если сделать селекцию слишком "жесткой" (не зря ведь биологам давно известно, что если осталось меньше десятка особей исчезающего вида, то этот вид сам по себе исчезнет из-за вырождения).

МГУА

Описанный в разделе алгоритмов распознавания образов метод группового учета аргументов так же относится к разряду эволюционных. Его можно представить как следующий цикл: Берем самый последний слой классификаторов. Генерируем из них по определенным правилам новый слой классификаторов (которые теперь сами становятся последним слоем). Отбираем из них F лучших, где F - ширина отбора (селекции). Если не выполняется условие прекращения селекции (наступление вырождения – инцухта), переходим на п. 1. Самый лучший классификатор объявляется искомым решением задачи идентификации. Как мы видим, налицо все признаки эволюционного алгоритма - отбор (селекция) и генерация нового поколения.

Генетический алгоритм (ГА)

Генетический алгоритм является самым известным на данный момент представителем эволюционных алгоритмов, и по своей сути является алгоритмом для нахождения глобального экстремума многоэкстремальной функции. ГА представляет собой модель размножения живых организмов. Для начала представим себе целевую функцию многих переменных, у которой необходимо найти глобальный максимум или минимум:

Для того чтобы заработал ГА, нам необходимо представить независимые переменные в виде хромосом. Как это делается? Как создать хромосомы?

Первым шагом будет преобразование независимых переменных в хромосомы, которые будут содержать всю необходимую информацию о каждой создаваемой особи. Имеется два варианта кодирования параметров: в двоичном формате; в формате с плавающей запятой.

В случае если мы используем двоичное кодирование, мы используем N бит для каждого параметра, причем N может быть различным для каждого параметра. Если параметр может изменяться между минимальным значением MIN и максимальным MAX, используем следующие формулы для преобразования:

Где g – целочисленные двоичные гены, r – эквивалент генов в формате с плавающей запятой. Хромосомы в формате с плавающей запятой, создаются при помощи размещения закодированных параметров один за другим.

Если сравнивать эти два способа представления, то более хорошие результаты дает вариант представления в двоичном формате (особенно, при использовании кодов Грея). Правда, в этом случае мы вынуждены мириться с постоянным кодированием/декодированием параметров. Как работает генетический алгоритм?

В общем, генетический алгоритм работает следующим образом. В первом поколении все хромосомы генерируются случайно. Определяется их "полезность". Начиная с этой точки, ГА может начинать генерировать новую популяцию. Обычно, размер популяции постоянен. Репродукция состоит из четырех шагов: селекции и трех генетических операторов (порядок применения не важен) кроссовер мутация инверсия

Роль и значение селекции мы уже рассмотрели в обзоре эволюционных алгоритмов. Кроссовер является наиболее важным генетическим оператором. Он генерирует новую хромосому, объединяя генетический материал двух родительских. Существует несколько вариантов кроссовера. Наиболее простым является одноточечный. В этом варианте просто берутся две хромосомы, и перерезаются в случайно выбранной точке. Результирующая хромосома получается из начала одной и конца другой родительских хромосом. Мутация представляет собой случайное изменение хромосомы (обычно простым изменением состояния одного из битов на противоположное). Данный оператор позволяет более быстро находить ГА локальные экстремумы с одной стороны, и позволяет "перескочить" на другой локальный экстремум с другой. Инверсия инвертирует (изменяет) порядок бит в хромосоме путем циклической перестановки (случайное количество раз). Многие модификации ГА обходятся без данного генетического оператора.

Очень важно понять, за счет чего ГА на несколько порядков превосходит по быстроте случайный поиск во многих задачах. Дело здесь видимо в том, что большинство систем имеют довольно независимые подсистемы. Вследствие этого, при обмене генетическим материалом часто может встретиться ситуация, когда от каждого из родителей берутся гены, соответствующие наиболее удачному варианту определенной подсистемы (остальные "уродцы" постепенно вымирают). Другими словами, ГА позволяет накапливать удачные решения для систем, состоящих из относительно независимых подсистем (большинство современных сложных технических систем, и все известные живые организмы). Соответственно можно предсказать и когда ГА скорее всего даст сбой (или, по крайней мере, не покажет особых преимуществ перед методом Монте-Карло) - системы, которые сложно разбить на подсистемы (узлы, модули), а так же в случае неудачного порядка расположения генов (рядом расположены параметры, относящиеся к различным подсистемам), при котором преимущества обмена генетическим материалом сводятся к нулю. Последнее замечание несколько ослабляется в системах с диплоидным (двойным) генетическим набором.

Эволюционное (генетическое) программирование Данные, которые закодированы в генотипе, могут представлять собой команды какой-либо виртуальной машины. В таком случае мы говорим об эволюционном или генетическом программировании. В простейшем случае, мы можем ничего не менять в генетическом алгоритме. Однако в таком случае, длина получаемой последовательности действий (программы) получается не отличающейся от той (или тех), которую мы поместили как затравку. Современные алгоритмы генетического программирования распространяют ГА для систем с переменной длиной генотипа.

Автоматический синтез технических решений

Каждый изобретатель, каждый творчески работающий конструктор ищут не просто новое, улучшенное ТР, а стремятся найти самое эффективное, самое рациональное, лучшее из лучших решений. И такие решения некоторым изобретателям удавалось находить. Это, например, конструкция книги, карандаша, гвоздя, брюк, велосипеда, трансформатора переменного тока, паровой машины и многих других ТО. Такие конструкции в первую очередь характеризуются тем, что они сотни или десятки лет массово производятся и используются без изменения, если не считать мелких усовершенствований. Наивысшие достижения инженерного творчества заключаются в нахождении глобально оптимальных принципов действия и структур ТО.

Поиск оптимальных структур

Постановка задачи параметрической оптимизации. Прежде чем рассматривать постановку задачи поиска оптимального ТР для заданного физического принципа действия, разберем задачу более низкого уровня, которую называют задачей поиска оптимальных значений параметров для заданного ТР или сокращенно - задачей параметрической оптимизации. Эти задачи неизбежно приходится решать при поиске оптимального ТР, а кроме того, они имеют и самостоятельное значение. Любое отдельное ТР, как правило, можно описать единым набором переменных (изменяемых параметров)

(1)

которые могут изменять свои значения в некотором гиперпараллелепипеде

(2)

Математическая модель проектируемого изделия ставит в соответствие каждому набору значений (1) некоторый критерий качества (функцию цели) F(х) и накладывает на переменные (1) дополнительные ограничения, представляемые чаще всего в виде системы нелинейных неравенств

(3)

Тогда задача поиска оптимальных параметров ТР состоит в нахождении такого набора (1), который удовлетворяет неравенствам (2) и (3) и обеспечивает глобальный экстремум критерию качества. Для определенности будем считать, что отыскивается минимум, и, если обозначим через D область допустимых решений, удовлетворяющих неравенствам (2), (3), получим задачу математического программирования в n-мерном пространстве: Найти точку такую, что:

(4)

Постановку задач структурной оптимизации обычно начинают с определения набора переменных по следующей методике. Задают такие переменные, чтобы они могли по возможности описать множество всех рациональных структур , которые в состоянии оценить существующая математическая модель в рассматриваемом классе ТО. 2. Просматривают и анализируют методы преобразования структур. Дополняют множество подмножествами новых структур, которые можно синтезировать и оценить с помощью существующей или доработанной математической модели. В результате строится расширенное множество рассматриваемых структур S и описывающий его набор переменных, который обозначим вектором А 3. Из вектора А выделяют вектор А' независимых переменных, которыми можно варьировать при поиске оптимальных структур. Для зависимых переменных задают алгоритм их определения через независимые переменные.

4. Вектор А' разделяют на вектор переменных , обеспечивающих изменение структуры, и вектор переменных , с помощью которых ставят и решают задачи параметрической оптимизации для заданной структуры. Вектор состоит из набора общих переменных , которые присутствуют при изменении любой структуры, и набора переменных , изменяющихся при переходе от структуры к структуре. При решении задачи параметрической оптимизации для заданной структуры используется только определенная часть переменных из набора . К задачам структурной оптимизации относится задача выбора оптимальной компоновки ТО.

Отметим некоторые особенности задач структурной оптимизации. Во-первых, почти всегда в этих задачах одновременно присутствуют и дискретные, и непрерывные переменные, т. е. задачи структурной оптимизации в общем случае относятся к смешанным задачам математического программирования. Во-вторых, при структурных преобразованиях изменяются число и характер переменных и соответственно функции ограничений и целевые функции. Что касается характера многосвязной области поиска, то отдельные подобласти или имеют различную размерность или (при совпадении размерности) образованы различными наборами переменных.

Алгоритм поиска глобального экстремума

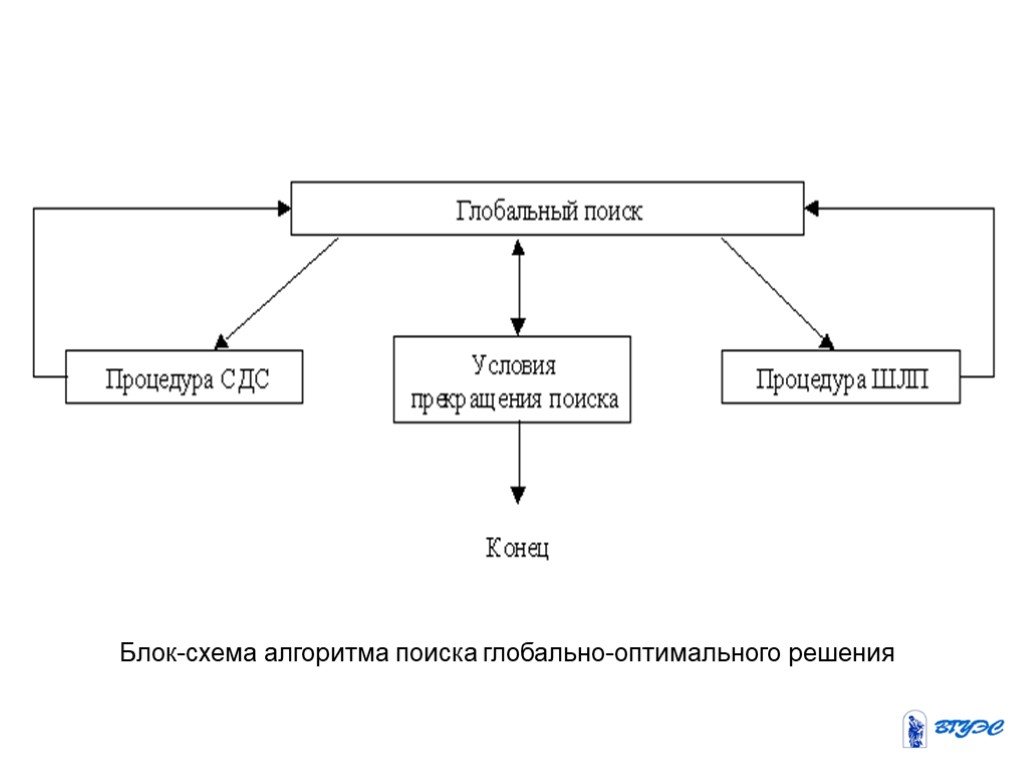
Алгоритм поиска глобально-оптимального решения можно использовать для решения задач как параметрической, так и структурной оптимизации. Укрупненная блок-схема алгоритма включает четыре процедуры: синтез допустимой структуры (СДС), обеспечивающий выбор допустимого решения из любой подобласти всей области поиска; 2) шаг локального поиска (ШЛП), обеспечивающий переход от одного решения к другому допустимому решению, как правило, той же структуры, но с улучшенным значением критерия; под шагом локального поиска можно понимать некоторый условный шаг по какому-либо алгоритму поиска локального экстремума (например, одна итерация по методу наискорейшего спуска); 3) глобальный поиск, управляющий работой процедур СДС и ШЛП; 4) проверка условий прекращения поиска, определяющая конец решения задачи

Блок-схема алгоритма поиска глобально-оптимального решения

В целом по процедуре СДС можно дать следующие рекомендации, направленные на повышение вероятности выбора допустимых структур и снижение объема вычислений по оценке недопустимых: способы выбора значений переменных должны содержать правила, отсекающие заведомо нерациональные и недопустимые значения переменных и их комбинации; ограничения следует проверять не после построения структуры в целом, а по возможности в процессе построения, что позволяет сократить лишнюю работу по ненужным построениям и в ряде случаев сразу внести поправки по устранению дефектов структуры; проверяемые ограничения должны быть упорядочены по снижению вероятности их нарушения; такое упорядочение иногда можно проводить автоматически в процессе решения задачи.

Процедуры ШЛП включают обычно способы изменения переменных, ориентированные на решение задач как структурной, так и параметрической оптимизации. Приведенные рекомендации по построению процедур СДС можно использовать и при построении способов локального изменения дискретных переменных. Для изменения непрерывных переменных, как правило, применяют различные алгоритмы локального поиска. Ниже указаны наиболее предпочтительные. Алгоритм конкурирующих точек Алгоритм случайного поиска в подпространствах

Алгоритм конкурирующих точек

В качестве процедуры глобального поиска используется алгоритм конкурирующих точек. В основе этого алгоритма лежит принцип эволюции популяции живых организмов, находящихся в ограниченном пространстве, например, на острове. В такой популяции резко обостряется конкуренция между отдельными особями. В связи с этим в основу алгоритма конкурирующих точек положены следующие положения: поиск глобального экстремума осуществляется несколькими конкурирующими решениями (точками); условия конкуренции одинаковых для всех решений; в определенные моменты некоторые "худшие" решения бракуются (уничтожаются); последовательный локальный спуск каждого решения (вначале грубый, затем более точный) происходит независимо от спуска других решений.

Конкуренция позволяет за счет отсева решений, спускающихся в локальные экстремумы, достаточно быстро находить глобальный экстремум в задачах, для которых значение функционала, осредненное по области притяжения глобального экстремума, меньше значения функционала, осредненного по всей области поиска, а область притяжения глобального экстремума не слишком мала. Алгоритм конкурирующих точек - один из наиболее простых и эффективных по сравнению с другими распространенными алгоритмами поиска глобального экстремума. Так, например, трудоемкость поиска (затраты машинного времени) по этому алгоритму на порядок меньше по сравнению с алгоритмом случайного перебора локальных экстремумов и на два порядка меньше по сравнению с методом Монте-Карло.