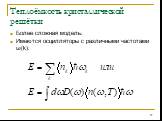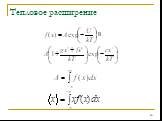Презентация "Физические свойства твёрдых тел" по физике – проект, доклад

Введение в физические свойства твёрдых тел

Лекция 6. Колебания кристаллической решётки. Фононы. Тепловые свойства твёрдых тел

Структура раздела

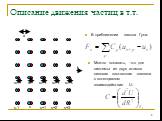
Общие замечания Описание движения частиц в т.т. Гармоническое приближение Выражение для смещений как функция времени и координат Закон дисперсии Зоны Бриллюэна Взаимодействие с Э.М. полем Теплоёмкость кристаллической решётки

Теплоёмкость кристаллической решётки Модели Дебая и Эйнштейна Плотность колебательных состояний и фактор Дебая-Уоллера Температура плавления. Формула Линдемана Тепловое расширение Теплопроводность

Общие замечания

Следующий шаг в изучении механических свойств т.т. Учёт дискретной структуры вещества Учёт квантования энергии колебаний Существующие теоретические подходы имеют свои ограничения (гармоническое приближение, взаимодействие между ближайшими соседями и т.д.) Теряется информация о непосредственной связи между механическим воздействием и откликом системы

Дискретный характер строения вещества оказывает влияние на свойства деформационных колебаний в кристалле Когда длина волны становится сравнимой с межатомным расстоянием, изменяется зависимость ω(k) (закон дисперсии) Скорость распространения колебаний становится функцией волнового вектора

Квантование колебаний приводит к тому, что теплоёмкость т.т. Стремится к нулю при Т0 Оно так же приводит к особенностям взаимодействия фононов с материальными частицами (нейтроны, электроны) и электромагнитными волнами Эти особенности заключаются в существовании неупругого рассеяния, когда происходит рождение или уничтожение кванта колебаний среды. При этом наблюдается скачкообразное изменение характеристик потока частиц, взаимодействующих с твёрдым телом

Описание движения частиц в т.т.

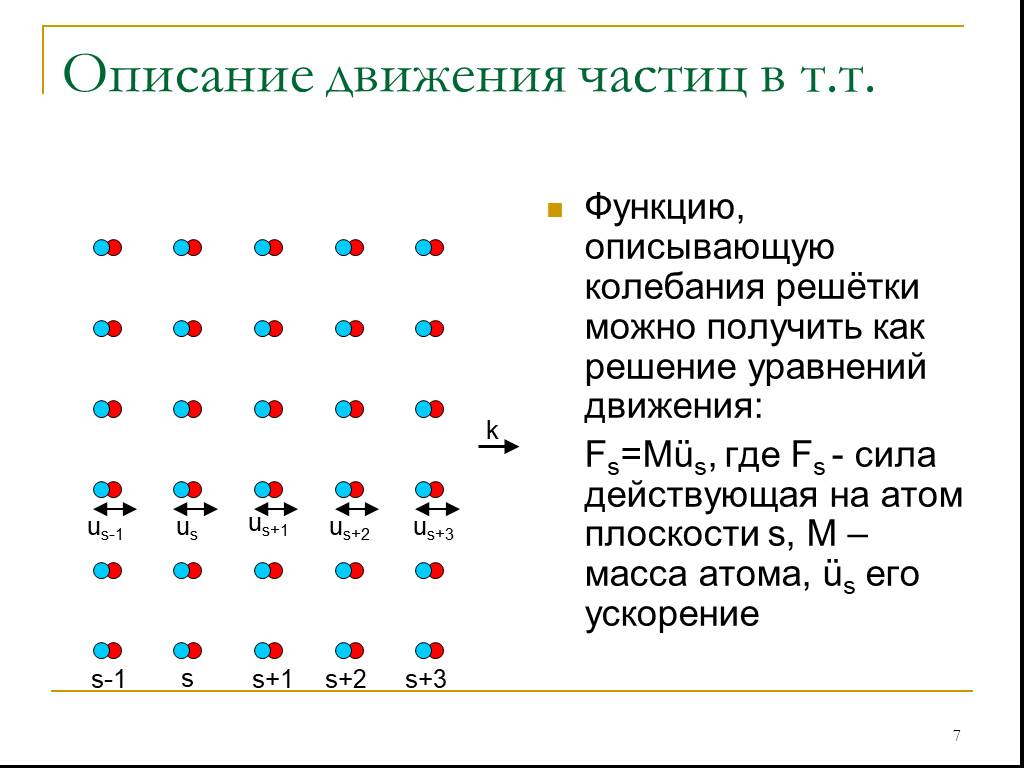
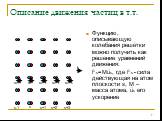
Функцию, описывающую колебания решётки можно получить как решение уравнений движения: Fs=Müs, где Fs - сила действующая на атом плоскости s, M – масса атома, üs его ускорение

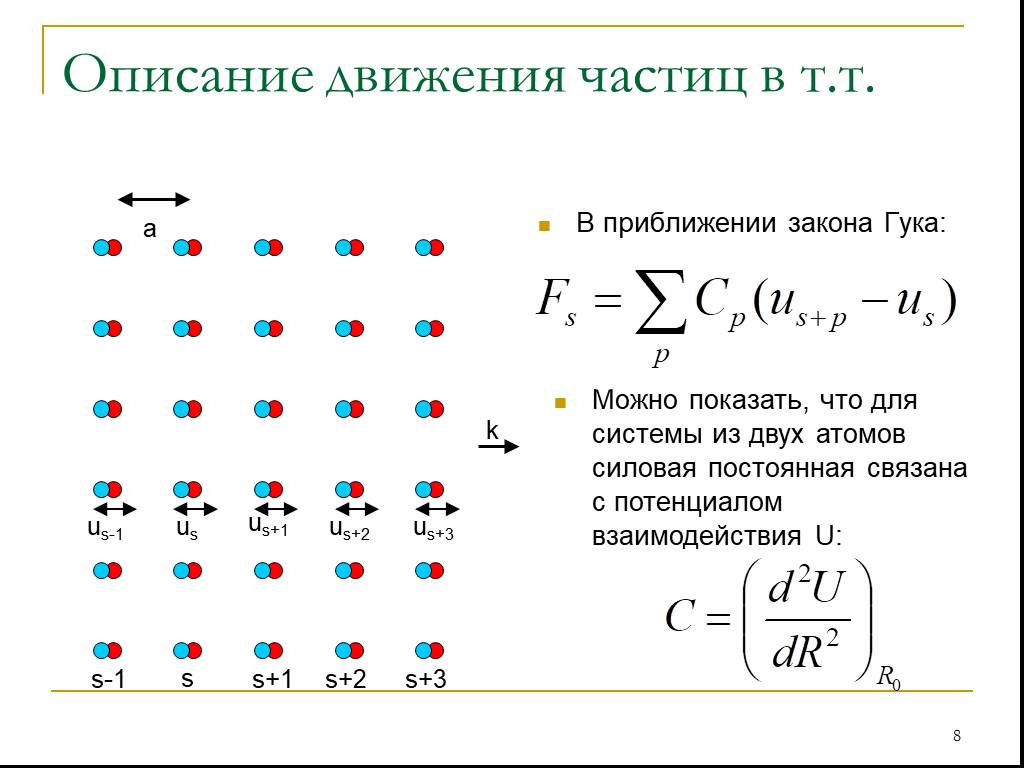
В приближении закона Гука:

Можно показать, что для системы из двух атомов силовая постоянная связана с потенциалом взаимодействия U:

a

Использование закона Гука соответствует гармоническому приближению Существует и другой подход к составлению уравнений движения:

Ws,p – тензорная величина. Имеет смысл силы, действующей на частицу s при смещении частицы р на up.

Решение уравнения движения ищем в виде:

Подставив это выражение в уравнение движения и учитывая, что Cp=C-p, получим закон дисперсии:

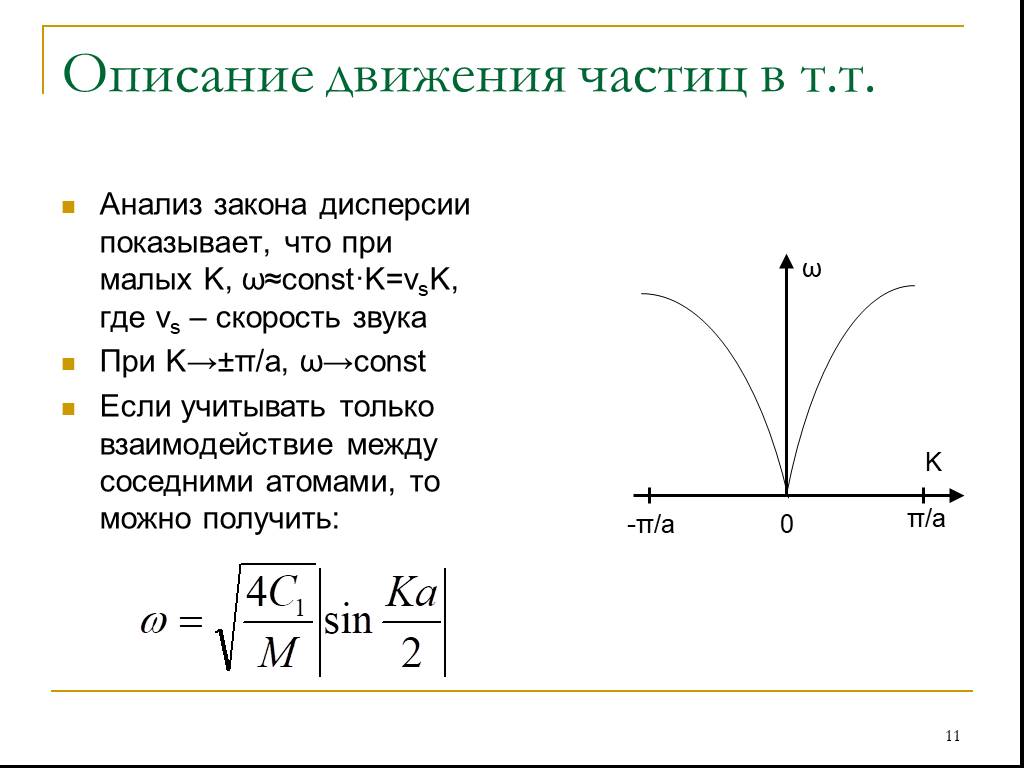
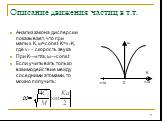
Анализ закона дисперсии показывает, что при малых K, ω≈const·K=vsK, где vs – скорость звука При K→±π/a, ω→const Если учитывать только взаимодействие между соседними атомами, то можно получить:

Область независимых значений волнового вектора K: Эта область называется (первой) зоной Бриллюэна Значения K, лежащие за её пределами, можно привести к значениям, лежащим в первой зоне, прибавляя (вычитая) nπ, где n – целое число. Эти значения являются физически идентичными

Закон дисперсии фононов можно определить экспериментально по рассеянию нейтронов Зная закон дисперсии, можно вычислить силовые постоянные Cp:

Установлено, что в металлах межатомные силы могут быть достаточно дальнодействующими (р~20)

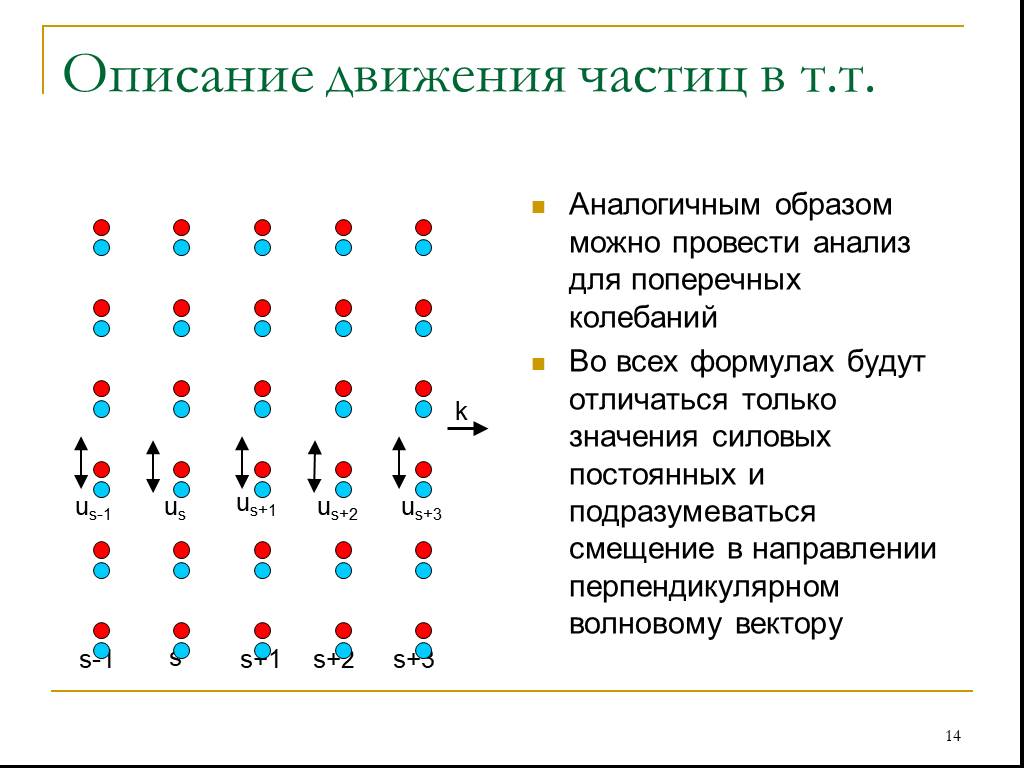
Аналогичным образом можно провести анализ для поперечных колебаний Во всех формулах будут отличаться только значения силовых постоянных и подразумеваться смещение в направлении перпендикулярном волновому вектору

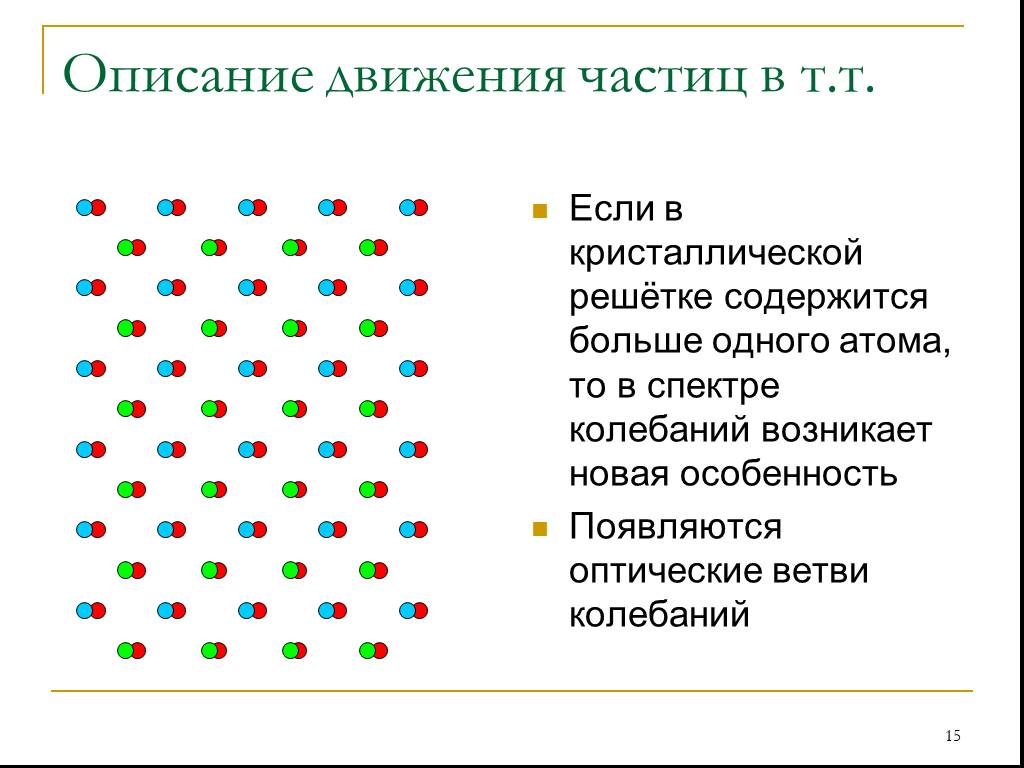
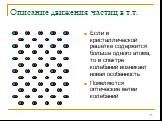
Если в кристаллической решётке содержится больше одного атома, то в спектре колебаний возникает новая особенность Появляются оптические ветви колебаний

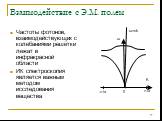
Взаимодействие с Э.М. полем

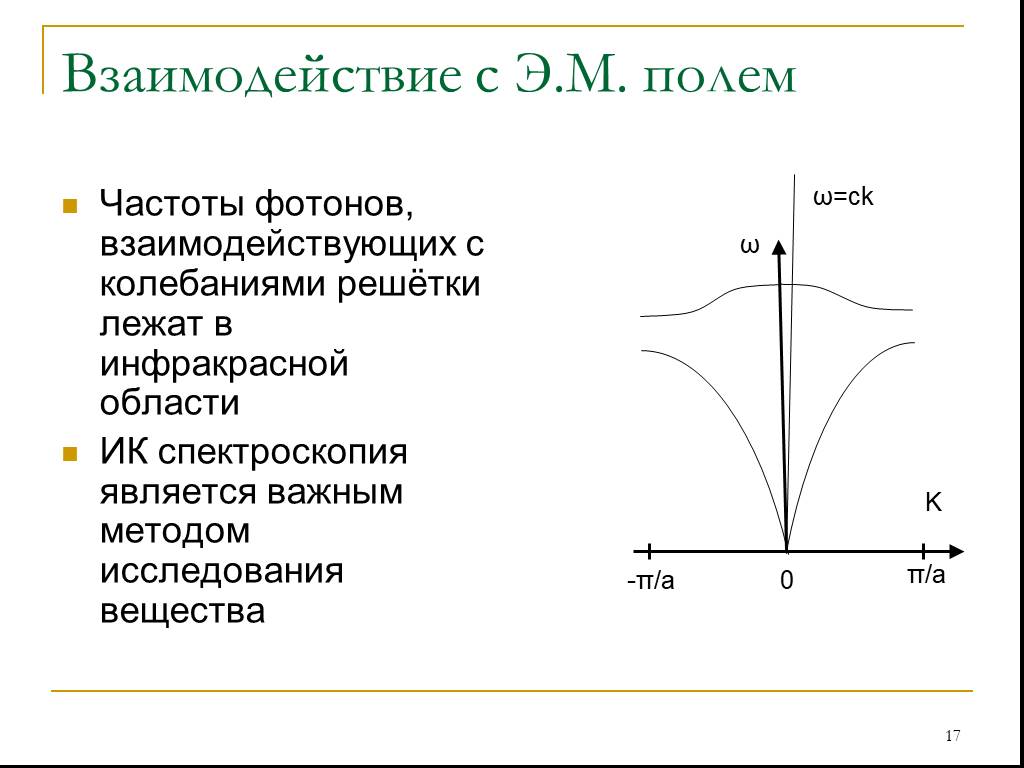
Оптические колебания имеют иной закон дисперсии, чем акустические. У них ω(0)≠0 Если атомы, входящие в элементарную ячейку несут избыточный заряд, то при их колебаниях возникают колебания дипольного момента. Это приводит к излучению электромагнитных волн С другой стороны, электромагнитное излучение может приводить к возбуждению колебаний решётки

Частоты фотонов, взаимодействующих с колебаниями решётки лежат в инфракрасной области ИК спектроскопия является важным методом исследования вещества

Если в элементарной ячейке содержится n атомов, то возникает 3n ветвей колебаний. 3 из них акустические. Остальные – оптические В кристаллах содержащих дефекты могут возникать дополнительные (локальные) колебания. Они могут так же проявляться в оптических спектрах т.т.

Использованное выше гармоническое приближение подразумевало разложение потенциальной энергии как функции координат атомов в ряд по малым смещениям этих атомов из положений равновесия

Нулевой член ряда от смещений не зависит и на результаты не влияет Первый член ряда, линейный по смещениям, в точности равен нулю, т.к. рассматривается состояние вблизи равновесия Разложение ограничивается квадратичным слагаемым

Важной особенностью гармонического приближения является представление колебаний кристаллической решётки в виде суперпозиции невзаимодействующих между собой колебательных мод Математически этот результат следует из того факта, что функция Гамильтона, описывающая колебания, является положительно определённой квадратичной формой

С помощью преобразований переменных такую форму можно привести к сумме слагаемых, не содержащих перекрёстных членов, а только квадраты смещений и импульсов (диагонализация) Уравнения движения можно получить из функции Гамильтона. Если она приведена к диагональному виду, то получается несколько уравнений движения, зависящих каждое от одной координаты

Такие координаты называются нормальными Недостатки этого подхода: Отсутствует механизм установления теплового равновесия Исчезает эффект теплового расширения Нельзя описать процесс теплопроводности Теплоёмкость не зависит от типа термодинамического процесса

Теплоёмкость кристаллической решётки

Различают теплоёмкости CP и CV В экспериментах определяют CP, в теоретических расчётах – CV разница между ними невелика: CP-CV=9α2BVΔT, где α – температурный коэффициент линейного расширения, V – объём, В – модуль всестороннего сжатия

Основные экспериментальные факты: При комнатной температуре теплоёмкости твёрдых тел близки к 3NkB, т.е. 25 Дж/(моль·К) Вблизи Т=0 теплоёмкость диэлектриков пропорциональна Т3, а металлов – Т

В состоянии теплового равновесия число фононов с частотой ω определяется с помощью формулы Планка: Энергия колебаний с частотой ω: Eω=ħω

Теплоёмкость кристаллической решётки. Модель Эйнштейна

Модель Эйнштейна: энергия Е системы N осцилляторов с частотой ω равна сумме их энергий Теплоёмкость:

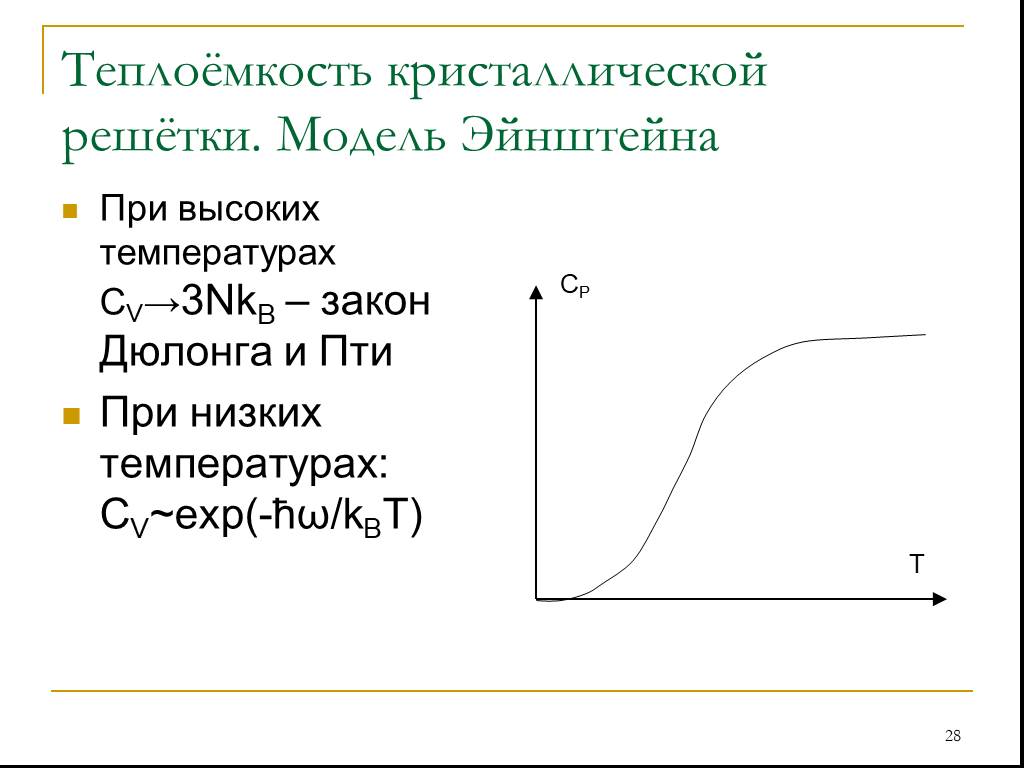
При высоких температурах CV→3NkB – закон Дюлонга и Пти При низких температурах: CV~exp(-ħω/kBT)

Более сложная модель: Имеются осцилляторы с различными частотами ω(k):

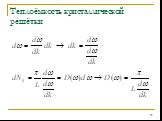
Теплоёмкость находится дифференцированием энергии по температуре Таким образом, надо знать функцию плотности (колебательных) состояний D(ω)

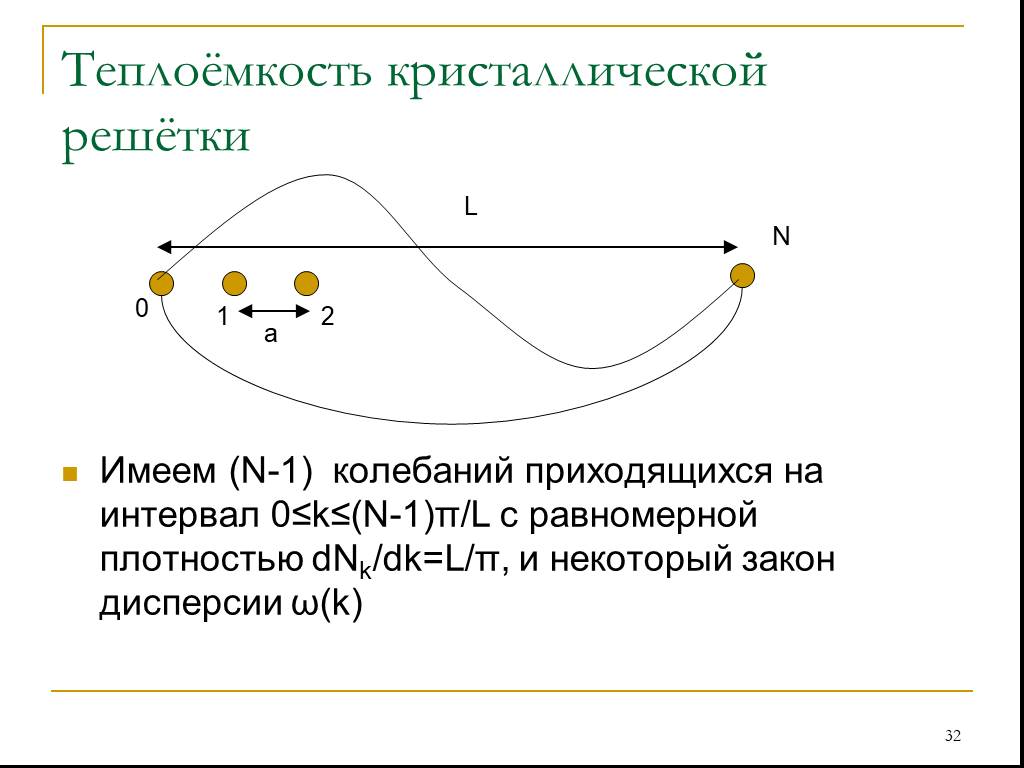
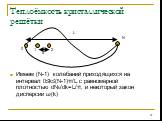
Нахождение D(ω) Представим одномерный кристалл как ограниченную цепочку атомов длины L Потребуем, чтобы в его объёме укладывалось целое число волн. Тогда, допустимые значения k=n2π/L, где n=0,1,…. Из-за дискретности структуры вещества существует верхнее ограничение на k и, следовательно, на n. k≤π/a=(N-1)π/L, где a – постоянная решётки, а N – число атомов

Имеем (N-1) колебаний приходящихся на интервал 0≤k≤(N-1)π/L с равномерной плотностью dNk/dk=L/π, и некоторый закон дисперсии ω(k)

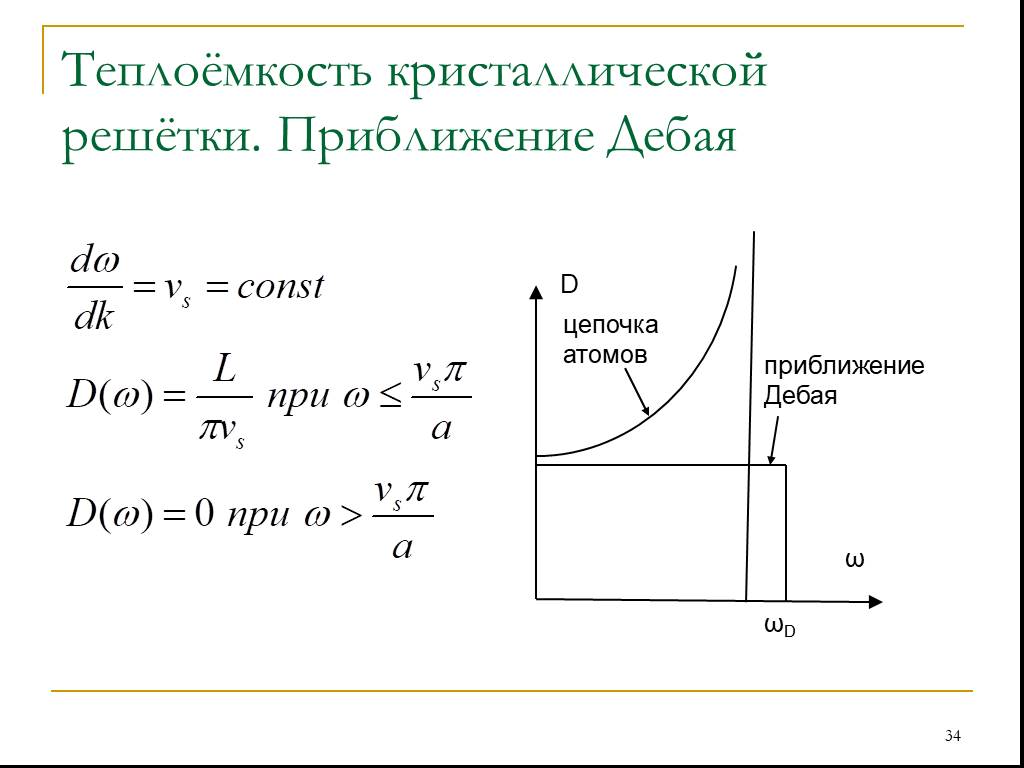
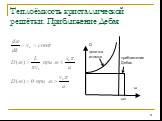
Теплоёмкость кристаллической решётки. Приближение Дебая

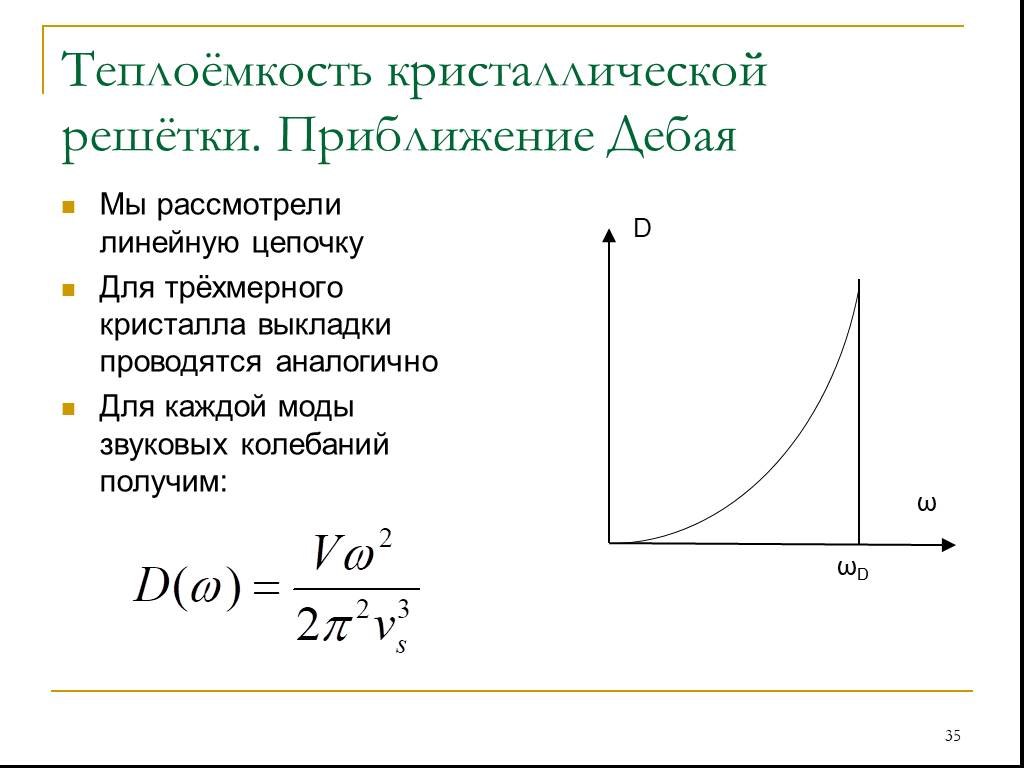
Мы рассмотрели линейную цепочку Для трёхмерного кристалла выкладки проводятся аналогично Для каждой моды звуковых колебаний получим:

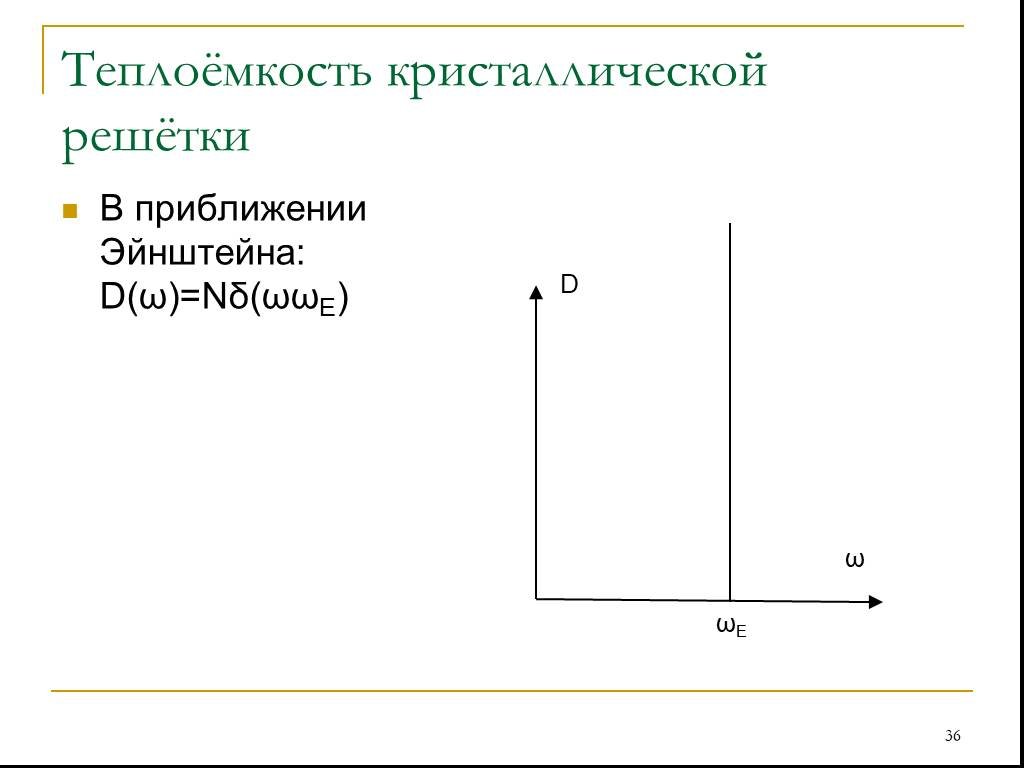
В приближении Эйнштейна: D(ω)=Nδ(ω­ωE)

Для практических целей выбирают некоторую дебаевскую частоту ωD, которая для данного конкретного вещества позволяет наилучшим образом согласовать теоретическую зависимость с экспериментальной зависимостью теплоёмкости от температуры Эти значения приводятся в справочниках Температура Дебая определяется из соотношения: ħωD=kBTD

Приближение Дебая относительно хорошо работает для структур не обладающих оптическими колебаниями Для оптических колебаний лучше работает модель Эйнштейна

Дифракция на кристалле

Рассеяние частиц или рентгеновского излучения на периодическом потенциале описывается матричными элементами переходов В случае идеальной решётки матричные элементы пропорциональны фурье-образу потенциала Рассеяние идёт в дискретных направлениях

Рассмотрим случай колеблющейся решётки Матричный элемент рассеяния можно представить в виде произведения фурье-образа атомного потенциала и структурного фактора

Положения атомов задаются векторами Rℓ

Это выражение подставляется в структурный фактор, который затем раскладывается в ряд по малым смещениям из положений равновесия Показывается, что происходит рассеяние в любом направлении. Его интенсивность определяется амплитудой колебаний с волновыми векторами, определённым образом связанными с волновыми векторами падающего и рассеянного излучения

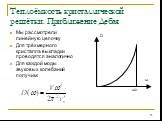
Фактор Дебая-Уоллера

Можно показать, что матричные элементы для упругого и неупругого рассеяния содержат множитель e-2W, называемый фактором Дебая-Уоллера Для его расчёта используется модель Дебая. При высоких температурах:

Аналогичные рассуждения используются при объяснении температурной зависимости эффекта Мёссбауэра и люминесценции в твёрдом теле При расчёте фактора Дебая-Уоллера можно так же найти величину среднего квадрата смещения атома из положения равновесия:

Формула Линдемана

Можно предположить, что плавление твёрдого тела происходит, когда амплитуда колебаний атомов начинает составлять некоторую долю xm от среднего значения параметра элементарной ячейки rs. Тогда, температуру плавления можно связать, с характеристическими постоянными xm=0,2-0,25

Тепловое расширение

Рассмотрим двухатомную молекулу с потенциалом взаимодействия U(x) Разложим потенциал в ряд Тейлора вблизи положения равновесия с точностью до членов четвёртого порядка: U(x)=U(0)+cx2-gx3-fx4 Используя распределение Больцмана, можно показать, что:

Коэффициент линейного теплового расширения α определяется как относительное изменение межатомного расстояния в расчёте на единицу изменения температуры Таким, образом, эта модель даёт линейную зависимость изменения длины от температуры и показывает связь константы линейного расширения с коэффициентом ангармоничности

Изменение частот колебаний

Представления о нормальных колебаниях являются следствием решения уравнений движения в гармоническом приближении При учёте слагаемого третьего порядка в разложении потенциала изменится вид уравнений движения

Решение уравнений движения можно искать методом последовательных приближений При этом появятся дополнительные решения в виде колебаний с комбинационными частотами: ωα±ωβ Амплитуды комбинационных частот пропорциональны произведениям амплитуд соответствующих нормальных колебаний aαaβ

При учёте членов разложения потенциала более высокого порядка появятся частоты, являющиеся комбинацией большего числа частот нормальных колебаний Ещё одним эффектом, обусловленным ангармоничностью, будет смещение частот колебаний осцилляторов

Теплопроводность

Экспериментально можно установить зависимость, связывающую поток тепла j с градиентом температуры В одномерном случае: j=KT/x, где K – коэффициент теплопроводности (с точностью до знака) В трёхмерном:

Явление теплопроводности не согласуется с представлениями о невзаимодействующих между собой колебаниях решётки (фононах) Можно сохранить понятие фононов дополнив его представлениями об их взаимодействии (рассеянии) Это соответствует учёту ангармоничности в уравнениях движения Кроме того, механизм взаимодействия фононов необходим для установления теплового равновесия между колебательными состояниями

В кинетической теории газов можно получить выражение: K=1/3Cvℓ, где C – теплоёмкость единицы объёма, v – средняя скорость частиц, ℓ – длина свободного пробега Эту формулу можно применить к твёрдым диэлектрикам, подразумевая под частицами фононный газ

Задача рассмотрения теплопроводности кристаллической решётки – сложная Установлено, что теплопроводность обусловлена такими взаимодействиями, в которых импульс фононов изменяется на вектор обратной решётки (процессы переброса)

Заключение

Дискретная структура вещества и квантование колебательной энергии приводят к ряду особенностей в свойствах твёрдого тела, обусловленных колебаниями кристаллической решётки Область независимых значений волнового вектора колебаний решётки называется зоной Бриллюэна

Существуют оптические и акустические колебания, отличающиеся законом дисперсии Использование гармонического приближения приводит к выводу о существовании невзаимодействующих «нормальных» колебаний – фононов Гармоническое приближение не описывает многие важные эффекты

При высоких температурах теплоёмкости твёрдых тел близки к 25 Дж/(моль·К) – закон Дюлонга и Пти При Т→0 теплоёмкость→0 В условиях теплового равновесия число фононов с определённой частотой описывается формулой Бозе-Эйнштейна

В модели теплоёмкости Эйнштейна учитывается лишь одна мода колебаний В модели Дебая учитываются различные колебательные моды с линейным законом дисперсии В общем случае для определения теплоёмкости т.т. надо знать функцию плотности состояний

Важным параметром, использующимся при описании различных свойств твёрдого тела, является температура Дебая При рассеянии излучения на кристалле возникает фон, обусловленный тепловым движением атомов решётки С увеличением температуры уменьшается интенсивность брэгговского рассеяния и резонансного поглощения/излучения

Тепловое расширение и теплопроводность обусловлены ангармоничностью колебаний частиц в т.т. Учёт ангармоничности приводит к изменению частот и конечному времени жизни колебаний В гармоническом приближении невозможно установление теплового равновесия между колебательными состояниями

Контрольные задания

Какое влияние оказывает дискретная структура вещества на механические колебания распространяющиеся в нём? В каких эффектах проявляется квантовый характер колебаний атомов в твёрдом теле? Чем отличаются оптические и акустические колебания решётки т.т.?

Сколько имеется акустических ветвей колебаний кристаллической решётки? Сколько имеется оптических ветвей колебаний кристаллической решётки? На чём основан метод ИК спектроскопии вещества?

В чём состоит гармоническое приближение? В чём заключается особенность результатов, получаемых при гармоническом приближении? Что такое нормальные колебания? Каковы недостатки гармонического приближения?

Какая теплоёмкость больше, CP или CV, почему? Почему пренебрегают разностью теплоёмкостей твёрдого тела при постоянном давлении и постоянном объёме? Как зависит теплоёмкость твёрдого тела от температуры при нормальных условиях?

Как ведёт себя теплоёмкость твёрдого тела при низких температурах? Что описывает функция распределения Бозе-Эйнштейна? Как она выглядит? В чём заключается модель теплоёмкости Эйнштейна? Какую температурную зависимость теплоёмкости предсказывает модель Эйнштейна?

Для чего используется функция плотности (колебательных) состояний? Как находится функция плотности (колебательных) состояний? В чём заключается модель теплоёмкости Дебая? Какой вид имеет функция плотности (колебательных) состояний в модели Дебая?

Что описывает фактор Дебая-Уоллера? Что описывает формула Линдемана? Какой вид имеет функция плотности (колебательных) состояний в модели Эйнштейна? Как определяются частота и температура Дебая? Какие эффекты возникают при учёте ангармоничности колебаний?

Конец лекции