Презентация "Суть постулатов Бора" по физике – проект, доклад

Постулаты Бора

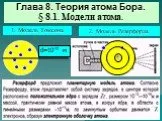
В 1913 г. Бор создал первую неклассическую теорию атома. В основе этой теории лежала идея связать в единое целое три результата, полученные в физике к тому времени: а) эмпирические закономерности линейчатого спектра атома водорода, выраженные в формуле Бальмера - Ридберга; б) ядерную модель атома Резерфорда, не допускающую классического истолкования; в) квантовый характер излучения и поглощения света.

Для решения этой задачи Бор, сохраняя классический подход к описанию поведения электрона в атоме, выдвинул три постулата, которые называются постулатами Бора. Сразу же заметим, что физический смысл этих постулатов не только не мог быть объяснен в классической физике, но, более того, находился в глубоком противоречии с классическим описанием движения электрона в атоме. Подлинный смысл и значение постулатов Бора вскрылись позднее, после создания квантовой механики. Теория Бора развивалась им для атома водорода и так называемых водородоподобных систем, состоящих из ядра с зарядом Ze и одного электрона, движущегося вокруг ядра. Примерами подобных систем являются однократно ионизованный гелий (Не+), двукратно ионизованный литий (Li++) и другие ионы. Такие системы называются также изоэлектронными водороду. Для водородоподобных систем все сериальные формулы, в частности формулы (28.5), вместо R содержат произведение RZ2.

Первый постулат Бора называется постулатом стационарных состояний. Он заключается в следующем: в атоме существуют некоторые стационарные состояния, не изменяющиеся во времени без внешних воздействий. В этих состояниях атом не излучает электромагнитных волн. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Несмотря на то, что электроны движутся ускоренно, они не излучают электромагнитных волн. В этом утверждении первого постулата Бора содержится отказ от выводов классической электродинамики об излучении энергии ускоренно движущимся зарядом. Второй постулат Бора называется правилом квантования орбит и утверждает, что в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные, квантованные значения момента импульса:

(28.6)

Здесь т — масса электрона, υ — его скорость, r — радиус круговой орбиты, = h/2π. Второй постулат Бора получает простое истолкование в квантовой механике. Аналогично тому, что мы имеем в задачах о потенциальном ящике и гармоническом осцилляторе, на длине круговой орбиты 2πr должно уложиться целое число длин волн де Бройля λ: 2υr = nλ.

Воспользуемся формулой, определяющей длину волны де Бройля. Тогда получим

что совпадает со вторым постулатом Бора (25.6).

Третий постулат Бора, или правило частот, устанавливает, что при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии. Излучение происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией. Этому соответствует переход электрона с орбиты, более удаленной от ядра, на более близкую к ядру орбиту. Поглощение атомом энергии сопровождается переходом атома из состояния с меньшей энергией в состояние с большей энергией. Этому соответствует переход электрона с орбиты, близкой к ядру, на более удаленную от ядра орбиту. Излучение или поглощение атомом электромагнитных волн приводит к изменению энергии атома, пропорциональному частоте этих волн. Если ΔE есть изменение энергии атома в результате излучения или поглощения электромагнитных волн, Eп и Eт — энергии атома в двух стационарных состояниях п и т, то правило частот можно записать так:

ΔE = Eп – Eт = hν (28.7)

При En > Em происходит излучение фотона, при En

Сравним между собой формулы (28.5) и (28.7). Сравнение приводит к очень важному результату. Оказывается, что энергия Eп атома водорода в некотором стационарном состоянии имеет вид

(28.8)

Таким образом, целые числа, которые входят в сериальную формулу (28.5), определяют дискретные, квантованные значения энергии атома водорода в соответствующих состояниях. Энергетические уровни атома водорода обратно пропорциональны квадратам целых чисел (при этом предполагается, что ядро атома неподвижно и энергия водородоподобной системы равна энергии движущегося электрона. Учет движения ядра приводит к незначительным изменениям результатов.). Целое число n, определяющее энергетический уровень атома водорода, называется главным квантовым числом. Энергетическое состояние, соответствующее значению n = 1, называется основным или нормальным (невозбужденным) состоянием. Все состояния с n > 1 называются возбужденными.

Знак минус в формуле (28.8) — отрицательные значения энергетических уровней — означает, что электрон испытывает силу притяжения к ядру, он связан с ним кулоновской силой притяжения.

Абсолютное значение величины Еп в формуле (28.8) является энергией связи электрона в атоме, находящегося в состоянии п. Под энергией связи электрона в атоме следует понимать величину работы, которую нужно совершить, чтобы оторвать электрон от атома, т. е. ионизовать атом. Иногда применяется термин: «энергия ионизации атома из данного состояния». Очевидно, что энергия ионизации из данного состояния равна по абсолютной величине энергии связи электрона в атоме в этом состоянии. Например, в основном состоянии (при n = 1) энергия ионизации Eион атома водорода составляет 13,53 эВ. Энергия электрона в основном состоянии Е1 = - 13,53 эВ. На приведенном выше рис. 28.3 слева указаны значения энергетических уровней атома водорода в электронвольтах. Сближение уровней при увеличении главного квантового числа п соответствует тому, что при n→∞ энергия Еп→0. Значение Е∞ =0 соответствует ионизации атома. Стрелками на рис. 28.3 указаны переходы, соответствующие излучению различных серий спектральных линий.

Квантование энергии и вычисление постоянной Ридберга в теории Бора

Постулаты, выдвинутые Бором, позволили ему теоретически рассчитать спектр водорода и ионов, содержащих один электрон, движущийся вокруг ядра. Задача состояла в теоретическом выводе формулы (28.8) и вычислении постоянной Ридберга, измеренной на опыте с большой точностью. Бор считал, что электрон в атоме водорода движется по круговой орбите радиуса r. На такой траектории его удерживает кулоновская сила притяжения электрона к ядру, играющая роль центростремительной силы:

(28.9)

или, так как υ = ωm, где ω — угловая скорость электрона,

Возведем в квадрат обе части соотношения (28.6), заменив в нем υ на ωr:

Поделим почленно друг на друга левые и правые части двух последних формул. Тогда получим

(28.10)

Радиусы орбит электрона в атоме водорода (Z = l) прямо пропор-циальны квадратам главного квантового числа. В частности, радиус первой орбиты при п = 1, называемый первым боровским радиусом, равен

Первый боровский радиус принят за единицу длины в атомной физике.

Энергия электрона в атоме водорода (или соответствующем ионе) складывается из кинетической энергии К и потенциальной энергии U притяжения электрона к ядру:

(28.11)

Здесь мы использовали формулу (28.9), а также то, что потенциальная энергия притяжения электрона к ядру отрицательна и имеет вид

На рис. 28.4 изображена графически зависимость U(r) для электрона в поле ядра с зарядом Ze. Ядро находится в начале координат. Подставим в (28.11) выражение для r (см. (28.10)). Получим

Рис. 28.4 (28.12)

Нетрудно заметить, что, кроме использования постулатов Бора, вывод формулы (28.12) носит чисто классический характер. Все описание поведения электрона в атоме проводится так, как если бы это была обычная классическая частица. В этом проявляется непоследовательность теории Бора.

Сравнивая формулы (28.8) и (28.12) и полагая для водорода Z = 1, получим выражение для постоянной Ридберга:

(28.13)

Итак, для водородоподобного иона энергия в некотором стационарном состоянии имеет вид (ср. с (28.8))

(28.14)

а волновые числа спектральных линий выражаются формулой (ср. с (28.5))

(28.15)

Опыты Франка и Герца

Первый и третий постулаты Бора были экспериментально подтверждены в опытах Франка и Герца, поставленных в 1913 г. В этих опытах изучалось прохождение через газы пучка электронов, ускоренных в электрическом поле. Первые опыты были проведены с прохождением электронов через пары ртути. Схема опытов изображена на рис. 28.5. В стеклянный сосуд, в котором находились пары ртути при давлении около 13,3 Па, помещались накаленный катод К, испускающий электроны, анод А, соединенный

с гальванометром G, и сетчатый электрод S. Между катодом и сеткой создавалось электрическое поле, ускоряющее электроны до энергии еφ1 где φ1- разность потенциалов между катодом и сеткой, е - заряд электрона. Между сеткой и анодом создавалось слабое замедляющее поле с разностью потенциалов φа не более 0,5 В.

Рис. 28.5

При прохождении электронов через пары ртути происходят соударения электронов с атомами ртути. Столкновения электронов с атомами могут быть двух типов. Первый тип столкновений — упругие соударения, в результате которых скорости и энергии электронов не изменяются, а лишь происходят изменения направлений скоростей электронов. Второй тип столкновений — неупругие соударения, при которых электроны теряют свою энергию и передают ее атомам ртути. Упругие соударения электронов с атомами ртути не могут воспрепятствовать электронам попадать на анод. Ускоряющее электрическое поле между К и S по мере возрастания разности потенциалов φ1 должно вызывать возрастание анодного тока в трубке, и упругие столкновения не могут нарушить этой закономерности. Неупругие столкновения могут явиться причиной практически полного отсутствия анодного тока. В самом деле, если электроны при неупругом столкновении с атомами ртути потеряют свою энергию настолько, что они не смогут преодолеть слабого

задерживающего поля между сеткой S и анодом А, анодный ток должен практически упасть до нуля.

По первому постулату Бора, атом ртути не может принять от электрона любую порцию энергии. Атом может воспринять лишь такую энергию, которой будет достаточно для перехода атома в одно из возбужденных энергетических состояний. Ближайшим к основному, невозбужденному состоянию атома ртути является возбужденное состояние, отстоящее от основного по шкале энергий на 4,86 эВ. До тех пор, пока электроны, ускоряемые полем, не приобретут энергию еφ1 = 4,86 эВ, они испытывают только упругие столкновения с атомами, не теряют своей энергии, достигают анода и анодный ток возрастает. Как только энергия электрона достигнет значения 4,86 эВ, может произойти неупругое соударение электрона с атомом ртути, в результате которого

электрон полностью отдаст свою энергию атому. Вся энергия электрона пойдет на переход атома ртути из нормального энергетического состояния в возбужденное. Очевидно, что такой электрон не сможет преодолеть слабого задерживающего поля между S и А и не попадет на анод.

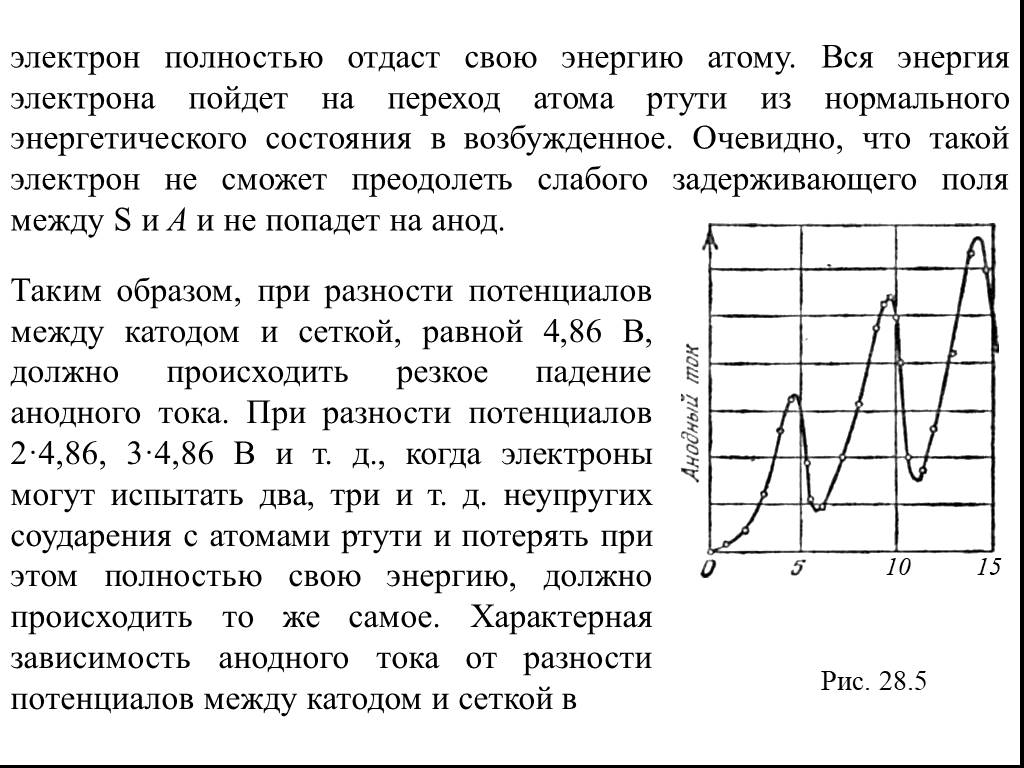
Таким образом, при разности потенциалов между катодом и сеткой, равной 4,86 В, должно происходить резкое падение анодного тока. При разности потенциалов 2·4,86, 3·4,86 В и т. д., когда электроны могут испытать два, три и т. д. неупругих соударения с атомами ртути и потерять при этом полностью свою энергию, должно происходить то же самое. Характерная зависимость анодного тока от разности потенциалов между катодом и сеткой в

10 15

опытах Франка —Герца приведена на рис. 28.6. При φ1 = 4,86 В, 9,72 В и 14,58 В происходит резкое падение анодного тока, подтверждающее справедливость первого постулата Бора.

В опытах Франка и Герца получил экспериментальное подтверждение третий постулат Бора (правило частот). Ртутные пары, находящиеся в трубке, с которой производились опыты, оказались источниками ультрафиолетового свечения с длиной волны 253,7 нм. Излучение ртутных паров связано с тем, что атомы ртути, возбужденные электронным ударом, находятся на возбужденном энергетическом уровне весьма непродолжительное время, порядка 10-8 с, и затем возвращаются на основной энергетический уровень. Согласно третьему постулату Бора, в момент перехода атома в нормальное состояние излучается квант энергии в виде фотона с энергией ΔΕ= hv. По известной величине ΔE = 4,86 эВ=4,86·е Дж, где е = 1,6-19 Кл — заряд электрона, можно вычислить длину волны испускаемого света:

Этот результат полностью согласуется с экспериментом: ртутные пары излучали главным образом именно эту длину волны. Помимо теоретического истолкования линейчатых спектров водородоподобных систем, теория Бора позволила объяснить физическую природу так называемых характеристических рентгеновских лучей и ряд других явлений, изложение которых выходит за нашего курса. Теория Бора сыграла огромную роль в создании атомной физики. В период ее развития (1913—1925 гг.) были сделаны важные открытия, часть из которых рассмотрена в лекциях. Особенно велика роль теории Бора в развитии атомной, а частично и молекулярной спектроскопии — учения о спектрах атомов и молекул. С помощью теории Бора огромный экспериментальный материал о спектрах атомов и молекул был систематизирован и сведен к полуэмпирическим закономерностям.

Однако, наряду со значительными успехами, в теории Бора сразу же обнаружились существенные недостатки. Основным из них была внутренняя противоречивость теории Бора. Она являлась соединением классической физики с квантовыми постулатами, противоречащими этой физике. Наиболее серьезной неудачей теории Бора явилась абсолютная невозможность с ее помощью создать теорию атома гелия и вообще любых систем, содержащих ядро и более одного электрона. Дальнейшее развитие физики показало, что теория Бора, правильно объяснившая одни факты и неспособная истолковать ряд других, представляла собой определенный переходный этап на пути создания последовательной теории атомных и ядерных явлений. Такой последовательной теорией явилась квантовая механика, некоторые основы которой мы уже рассмотрели в предыдущих лекцияъ, а также рассмотрим в дальнейшем.