Конспект урока «Сложение двузначных чисел: 32 + 28» по математике для 7 класса

М-2, часть 1

Урок 7.

Тип урока: ОНЗ.

Тема: «Сложение двузначных чисел: 32 + 28».

Автор: Мазурина С.Е. (НОУ «Школа Сотрудничества», г. Москва).

Основные цели:

1) Сформировать умение складывать двузначные числа в случаях, когда сумма – круглое число.

2) Актуализировать умение складывать двузначные и однозначные числа, сумма которых является круглым числом; тренировать умение записывать сложения столбиком.

3) Тренировать навыки устного счёта, умение решать задачи на нахождение части, целого, на разностное сравнение.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, аналогия, обобщение.

Демонстрационный материал:

1

На добрый путь всегда готовым будь!

) карточка с высказыванием:

2) изображение мышки:

3) таймер или песочные часы;

4

32 + 28

5) карточка с темой:

6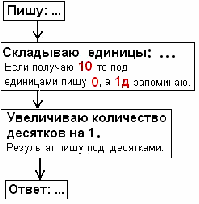) алгоритм сложения двузначного числа с однозначным в столбик (из урока 2-1-6):

Складываю десятки: …

7) отдельная карточка для уточнения алгоритма:

8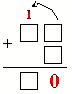) опорный сигнал сложения двузначного и однозначного чисел в столбик (из урока 2-1-6):

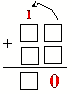
9) опорный сигнал сложения двузначных чисел в столбик:

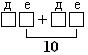
10) карточка с опорным сигналом для распознавания нового типа примеров:

Р

1) листы с заданием для актуализации:

2) чистого листа в клетку на каждого;

3) графические модели: «Треугольники и точки»;

4) алгоритм сложения двузначного и однозначного чисел в столбик на отдельных карточках и одна чистая карточка для уточнения алгоритма (по количеству групп);

5) «листочки настроения»:

Ход урока:

1. Мотивация к учебной деятельности:

Цель:

1) создать условия для возникновения внутренней потребности включения в учебную деятельность путём обсуждения высказывания и появления героя-помощника;

2) актуализировать требования к ученику со стороны учебной деятельности;

3) установить тематические рамки урока: новый приём сложения двузначных чисел.

Организация учебного процесса на этапе 1:

Открыть на доске карточку с высказыванием:

На добрый путь всегда готовым будь!

– Прочитайте слова, написанные на доске. Как вы их понимаете? (…)

– И вы, как всегда, отправитесь в добрый путь за знаниями. Расскажите, что ждёт вас в пути? (Сначала мы повторим необходимое, потом будет задание с чем-то новым. Мы попробуем его выполнить и, скорее всего, не получится. Мы подумаем, почему не получилось, поставим цель и сами построим способ…)

– А сопровождать вас в пути и помогать вам вместе со мной будет наша маленькая гостья – мышка.

Прикрепить изображение мышки на доску.

– Но прежде, давайте вспомним, с какими новыми примерами вы познакомились на прошлом уроке? (На сложение двузначного и однозначного чисел, когда в сумме получается круглое число.)

– Сегодня на пути к знаниям вы продолжите изучать тему «Сложение двузначных чисел».

2. Актуализация и пробное учебное действие.

Цель:

1) актуализировать умение складывать двузначные и однозначные числа, сумма которых является круглым числом; тренировать умение записывать сложение столбиком;

2) активизировать мыслительные операции: сравнение, анализ, аналогия, обобщение;

3) актуализировать норму пробного действия;

4) организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;

5) создать условия для фиксации учащимися возникшего затруднения в выполнении пробного действия или его обосновании.

Организация учебного процесса на этапе 2:

1) Сложение двузначного числа и однозначного, когда сумма – круглое число.

– Ребята, покажите мышке, что вы умеете работать самостоятельно, и работаете быстро. Я раздам листочки с заданием для каждого, а вы должны по моей команде за 30 секунд выполнить задание, в котором надо решить примеры. Запишите только ответы!

76 + 4 = 25 + 5 = 43 + 7 =

– Внимание! Начали!

Учитель включает таймер.

– Стоп! Проверим первый пример. Расскажите способ его решения. (Складываем единицы:

6 + 4 = 10. Количество десятков увеличиваем на 1, в разряде единиц запишем 0. Ответ – 80.)

– Найдите в своих опорных конспектах соответствующий эталон и покажите.

После показа эталона детьми учитель вывешивает соответствующий эталон на доску:

– Если есть неверные ответы – исправьте.

Аналогично разбирается ход решения второго и третьего примеров.

– Итак, какой способ решения примеров я выбрала для повторения? (Способ сложения двузначного числа с однозначным, когда при сложении единиц получается 10.)

2) Задание для пробного действия.

– Что будет дальше на вашем пути? (Задание, в котором будет что-то новое.)

– Верно. Задание – решить пример. Рассмотрите пример и скажите, что в нём для вас ново.

Открыть на доске: 32 + 28.

– Какое действие надо выполнить? (Сложение.)

–Какие числа надо сложить? (Двузначные.)

Повесить на доску часть опорного сигнала:

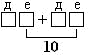–Чем этот пример похож на примеры на карточке? (При сложении единиц получается 10.)

Дополнить опорный сигнал:

–Что же в этом примере для вас ново? (Мы ещё не складывали двузначные числа, когда при сложении единиц получается 10.)

– И как вы поступите, ведь вы такого типа примеры ещё не решали? (Мы попробуем его решить.)

– Пробуйте. Решите пример и запишите ответ на листе в клетку.

– Назовите ответ примера. (50; 60; …)

Выписать на доску все варианты ответов детей.

Не исключена вероятность того, что, все учащиеся решат пример одинаково верно, поэтому далее предложены два варианта ответов детей: первый – если есть разные варианты ответов, второй – если все решили одинаково.

– Что же получилось? (Мнения разделились. Все решили одинаково.)

– Как (с помощью какого эталона) доказать, кто прав (что вы правы)? (Такого эталона нет.)

– Чего же вы не смогли сделать? (Мы не смогли решить пример 32 + 28. Мы не можем доказать, что решили пример верно.)

3. Выявление места и причины затруднения.

Цель:

1) создать условия для проведения учащимися пошагового анализа своих действий с опорой на эталон;

2) организовать фиксацию учащимися шага, на котором возникло затруднение;

3) организовать выявление учащимися причины затруднения.

Организация учебного процесса на этапе 3:

– Вы зафиксировали, что у вас есть затруднение, значит, … (Надо остановиться и подумать.)

– Какое задание вы выполняли? (Решали пример 32 + 28.)

– Что в этом типе примера было для вас ново? (Мы не складывали двузначные числа, когда при сложении единиц получается 10.)

– На какой эталон вы опирались, решая этот пример? (На эталон сложения двузначного числа с однозначным, когда при сложении единиц получается 10.)

– Расскажите, опираясь на этот эталон, как вы действовали. И назовите место, где вы засомневались. (…)

– Почему же возникло затруднение? (У нас нет нужного способа для решения примеров такого типа.)

4. Построение проекта выхода из затруднения.

Цель:

1) сформулировать цель учебной деятельности;

2) согласовать тему урока;

3) выбрать способ и средства для построения нового знания.

Организация учебного процесса на этапе 4:

– Что же вам следует выяснить? (Способ сложения двузначных чисел, когда при сложении единиц получается 10.)

– Как же тогда назвать урок, чтобы зафиксировать эту цель? (Сложение двузначных чисел, когда при сложении единиц получается 10.)

–

32 + 28

Повесить карточку с темой на доску:

– Итак, вам необходимо построить способ решения таких примеров. Что вам поможет (какие средства)? (Графические модели, запись в столбик, …)

– Чем сначала воспользуетесь? (Графическими моделями.)

– А потом? (Запишем решение этого примера в столбик.)

– А вы будете строить новый алгоритм или дополните уже известный? (Можно использовать алгоритм сложения двузначного и однозначного числа, но нужно его немножко изменить.)

Учитель может на доске зафиксировать план действий.

5. Реализация построенного проекта.

Цель:

1) создать условия для построения детьми нового способа решения примеров на сложение двузначных чисел, для случая 32 + 28, с использованием графических моделей;

2) применить новый способ действий для решения примера, вызвавшего затруднение;

3) зафиксировать новый способ действия в речи и с помощью эталона;

4) зафиксировать преодоление возникшего затруднения.

Организация учебного процесса на этапе 5:

– Итак, действуем по плану. Что сначала? (Выложим графическую модель примера и решим его с помощью графических моделей.)

Один учащийся на доске, остальные – на партах.

– По какому правилу будем складывать? (Десятки с десятками, единицы с единицами.)

–Что получилось? (При сложении десятков получилось 5 десятков, а при сложении единиц – 10.)

– Что же можете теперь сделать? (Заменить 10 единиц десятком.)

–Отлично! Значит, чем вы можете заменить 10 единиц на графической модели? (Одним десятком.)

– Сделайте это.

– Что вы заметили? (В ответе получилось круглое число, количество десятков увеличилось на один.)

– Значит, какой ответ этого примера? (60.)

– Что дальше по плану? (Запишем решение этого примера в столбик.)

О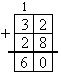дин учащийся у доски с объяснением, остальные работают в тетрадях.

– Скажите ещё раз, чем этот пример отличается от примеров, которые вы научились решать на предыдущем уроке? (Мы складывали двузначное число с однозначным числом, а в этом примере оба слагаемых двузначные.)

– Что дальше? (Надо изменить известный алгоритм сложения двузначного числа с однозначным числом.)

Раздать алгоритм сложения двузначного и однозначного чисел в столбик на отдельных карточках с одной чистой карточкой.

Разделить детей на группы по 3-4 человека, как это принято в классе.

– Посовещайтесь в группах и уточните алгоритм, вписав недостающий шаг на чистую карточку.

- Что надо помнить при работе в группах? (…)

Учащиеся воспроизводят правила работы в группах.

– Посмотрим, что у вас получилось.

Каждая группа представляет дополненный алгоритм. В ходе обсуждений выбирается лучший вариант и помещается на доску. В итоге алгоритм должен принять примерно такой вид:

–Как же дополнить опорный сигнал сложения в столбик? (Добавим еще один квадрат, обозначающий десятки, во второе слагаемое.)

Учитель достраивает опорный сигнал 6 урока со слов детей (дорисовывает квадрат).

– Дополните эталон сложения в столбик в тетрадях для опорных конспектов. (Если нет пособия «Построй свою математику».)

Если пособие «Построй свою математику» есть, то раздать детям соответствующий лист.

6. Первичное закрепление с проговариванием во внешней речи.

Цель:

создать условия для выполнения учащимися типовых заданий на использование изученного способа действия с проговариванием во внешней речи.

Организация учебного процесса на этапе 6:

– Как вы думаете, чем следует заняться дальше? (Надо потренироваться в решении примеров на новый способ.)

1) № 3, стр. 12.

– Откройте учебник на странице 12. Посмотрите, наша мышка встречает нас там. Она хочет поработать с вами и порадоваться вашим успехам. Выполните № 3. Прочитайте задание.

Задание:

Реши примеры по образцу. Что ты замечаешь? Составь и реши аналогичный пример.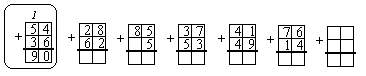

– С какого разряда начинаете складывать? (С разряда единиц.)

– Объясните решение первого примера. (54 + 36. Единицы записаны под единицами, десятки под десятками. Начинаю складывать с разряда единиц: 4 + 6 = 10. Ноль пишу под единицами, один десяток запоминаю: записываю 1 над разрядом десятков. Складываю десятки: 5 + 3 = 8, к сумме прибавляю 1, получится 9. Пишу 9 под разрядом десятков. Ответ 90.)

– Остальные примеры решите в парах, проговаривая способ, который используете при выполнении задания.

Далее решаются остальные примеры до тех пор, пока дети не заметят закономерность. В момент, когда дети заметили, что во всех примерах ответ 90, диалог построить следующим образом:

– Что вы заметили? (Во всех примерах ответ 90.)

– Можно ли утверждать, что и в остальных примерах ответ тоже 90? (Нет, здесь нет никакой закономерности.)

– Проверьте, будет ли ответ таким же в остальных примерах, а затем придумайте и решите аналогичный пример.

Оставшиеся примеры распределяются по вариантам. Тот, кто за отведённое время (1–2 минуты) успеет выполнить задание, в оставшееся время придумывает и решает свой пример.

– Расскажите друг другу в паре, как вы решали один из примеров.

– Отлично, мышка за вас очень рада.

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися типовых заданий на нахождение примеров нового вида и на применение нового способа действий;

2) организовать самопроверку учащимися своих решений по эталону для самопроверки;

3) создать (по возможности) ситуацию успеха для каждого ребёнка.

Организация учебного процесса на этапе 7:

– Давайте порадуем мышку тем, что покажете ей, как вы умеете самостоятельно справляться с более трудными заданиями, а заодно проверите свои силы в решении примеров на новый вычислительный приём.

– Какой приём был для нас новым на сегодняшнем уроке? (Сложение двузначных чисел, когда при сложении единиц получается 10.)

– Выполните № 5 (а), стр. 13.

Задание:

Выбери и реши примеры на новый вычислительный приём:

34 + 46 89 – 19 62 + 18 56 – 14

75 + 12 21 + 39 45 + 25 27 + 53

– Прочитайте задание. (Выбери и реши примеры на новый вычислительный приём.)

1) – Задание состоит из двух частей. Что надо сделать сначала? (Выбрать примеры на новый вычислительный приём.)

– Выполните эту часть задания самостоятельно, поставив в учебнике галочки рядом с выбранными вами примерами.

– Проверьте.

О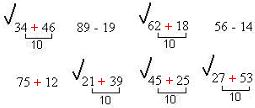ткрыть на доске эталон к этой части задания.

– Какие трудности возникли при выполнении? (Не обратили внимание на знак, не сложили единицы, чтобы узнать тип примера, …)

– Как вы действовали, выполняя поиск примеров на новый вычислительный приём? (Мы сначала смотрели на знак – «+», затем складывали единицы. Если при сложении единиц получалось 10, то ставили галочку, так как пример нашего нового типа.)

– Исправьте, у кого неверно были найдены примеры нового типа.

– У кого всё получилось? Нарисуйте на полях учебника улыбку.

2) – Прочитайте вторую часть задания. (Решить примеры на новый вычислительный приём.)

– Выберите любые два примера и решите их в тетради самостоятельно.

– Проверьте.

Открыть на доске эталон решения примеров.

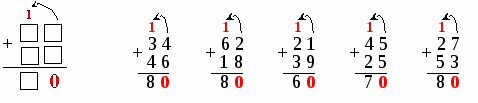
Проговаривается выполнение каждого примера во внешней речи.

– Какие трудности возникли при решении примеров? (Забыли увеличить количество десятков на 1, …)

– У кого всё получилось? Нарисуйте на полях тетради еще одну улыбку.

8. Включение в систему знаний и повторение.

Цель:

повторить решение составных задач на разностное сравнение, на нахождение целого и части.

Организация учебного процесса на этапе 8:

1) № 8, стр. 13.

– А теперь, мышка поведёт вас в сказку. Выполним сказочное задание. Это задача № 8 на странице 13. Прочитайте задачу.

Задание:

В некотором царстве всего два дома. В первом доме живут 7 детей и 6 взрослых, а во втором доме – 17 человек, из которых 9 взрослых. Составь по схеме вопросы к этому условию и ответь на них. Что ещё можно спросить?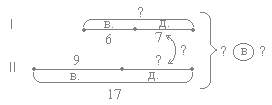

– Почему я назвала её сказочной? (Со слов «В некотором царстве…» начинаются сказки.)

– Что известно в задаче? (Имеется два дома. В первом доме живут 7 детей и 6 взрослых, а во втором доме – 17 человек, из которых 9 взрослых.)

– Что обозначает на схеме первый отрезок и его части? (Количество человек, живущих в первом доме. Первая часть обозначает количество взрослых, вторая – количество детей.)

– Что обозначает второй отрезок и его части? (Количество человек, живущих во втором доме. Первая часть – количество взрослых, вторая часть – количество детей.)

– Что обозначает двойная стрелка? (Надо узнать, на сколько детей в одном доме больше или меньше, чем в другом.)

– Что обозначает первый вопрос возле фигурной скобки? (Сколько всего человек живут в двух домах.)

– Что обозначает второй вопрос возле фигурной скобки? (Сколько взрослых живут в двух домах.)

– Какие вопросы можно поставить к этому условию? (Сколько всего человек живут в первом доме.)

– Ответьте на этот вопрос. (Чтобы ответить на этот вопрос, надо сложить количество взрослых и детей, живущих в первом доме, т.к. ищем целое. Мы можем сразу ответить на этот вопрос, т.к. известны обе части: 6 + 7 = 13 человек – живут в первом доме.)

– Какие ещё вопросы можно задать по схеме?

Далее устный разбор задач по каждому из вопросов идёт аналогично. Решение задач выполняется по усмотрению учителя в устной форме в зависимости от количества оставшегося времени.

(На сколько детей в первом доме меньше, чем во втором?)

(Сколько взрослых живут в двух домах вместе?)

(Сколько всего жителей в двух домах?)

(Сколько детей живут во втором доме?)

– Что ещё можно спросить?

(На сколько взрослых во втором доме больше, чем в первом?)

(Сколько детей живут в двух домах?) и т.д.

– Вы отлично справились со сложной задачей, а вот мышке пора в свою норку.

9. Рефлексия учебной деятельности на уроке.

Цель:

1) организовать самооценку учениками собственной учебной деятельности на уроке;

2) соотнести цель и результаты своей учебной деятельности и зафиксировать степень их соответствия;

3) зафиксировать в речи новый способ действий, изученный на уроке;

4) зафиксировать затруднения, которые остались, и способы их преодоления;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9:

– Но перед расставанием, давайте напомним ей, с какими примерами вы познакомились сегодня на уроке? (Сложение двузначных чисел, когда при сложении единиц получается 10, а в ответе – круглое число.)

– Как найти ответ в этих примерах? (В разряде единиц записать 0, а сумму десятков увеличить на 1.)

– У кого остались вопросы?

– У кого всё получилось?

– Оцените свою работу.

– Что вы скажем мышке на прощанье?

– Ребята, знаете, чтобы мышка не скучала в своей норке, давайте напишем ей письма. В них вы сообщите, как вы работали на уроке.

Раздать «листы настроения».

– Обведите на листочке слова, соответствующие вашему настроению, состоянию, и мы пошлём ваши «письма» мышке.

Собрать «листы настроения».

Домашнее задание:

 № 5 (б), 7 (на выбор), 9, стр.13;

☺ № 10, стр. 13.