Конспект урока «Степень с целым показателем и её свойства» по математике для 8 класса

Урок в 8 классе по теме «Степень с целым показателем и её свойства»

Цели урока:

• Образовательные: познакомить  учащихся  с понятием  степени  с  целым   показателем   и  её свойствами. Научить применять изученные понятия и свойства при вычислениях и преобразованиях.

• Развивающие: развивать умения применять теоретические знания на практике. Развивать познавательную активность, мышление, внимание и память, умение слушать товарища, математическую речь.

• Воспитательные: воспитание интереса к  математике, активности, аккуратности, дисциплинированности, умение общаться.

Ход урока.

1. Организационный этап.

2. Мотивация урока.

Надеюсь, что сегодня на уроке нас ждет и успех, и радость. И мы, работая в коллективе, покажем свою одарённость.

Будьте внимательны в течение урока. Думайте, спрашивайте, предлагайте – так как дорогой к истине мы будем идти вместе.

3. Актуализация изучения темы.

А начать наш урок я хотела бы с выяснения вопроса: встречался кто-нибудь из вас в повседневной жизни со словом «степень»? Давайте приведем примеры словосочетаний из жизни, в которых оно используется, и попытаемся с их помощью разобраться, что же в жизни означает слово «степень».

Ответы учащихся:

- точности

-степень усвоения

- качества знаний

Учитель

• Каким же близким по смыслу словом можно заменить слово “степень”?

• А где мы можем уточнить его значение?

Ученик :(в толковом словаре)

-  Степень  – это мера, сравнительная величина; уровень чего-нибудь.

- Слово “ степень ” находит широкое применение  и  в  математике .

Группа «Информаторы»

1. Дайте определение  степени   с   натуральным   показателем . ( Степенью  числа а  с   натуральным   показателем  n, большим 1, называется произведение n множителей, каждый из которых равен а.)

2. Как называется число, которое возводим в  степень ? (Число, которое возводим в степень, называют основанием)

3. Как называется число, в которое возводим степень? (Число, в которое возводим степень, называют  показателем )

4. Какое число получаем при возведении в степень положительного числа? (При возведении в степень положительного числа получаем положительное число)

5. Какое число получаем при возведении отрицательного числа с четным  показателем ? (При возведении отрицательного числа с четным  показателем  получаем положительное число)

6. Какое число получаем при возведении отрицательного числа с нечетным  показателем ? (При возведении отрицательного числа с нечетным  показателем  получаем отрицательное число)

Также устно, с полным объяснением, вычислить:

Решить №

4. Изучение нового материала.

Взгляните на число.

. Как вы думаете, это положительное или отрицательное число?

"Не верь глазам своим" - сказал бы Козьма Прутков тому, кто считает это число отрицательным.  И  сейчас мы разберемся, что вообще означает такая запись.

Историческая справка .(Информаторы) Отрицательные  показатели   степени  ввел еще в 15 веке  математик  Шюке. Англичанин Джон Валлис впервые рассмотрел вопрос о целесообразности употребления отрицательных  показателей . Исаак Ньютон стал применять их систематически. В одном из писем в 1676 г. Ньютон указал: "Как алгебраисты вместо АА, ААА  и  т.д. пишут А², А³ и т.д., так я ... вместо 1/а, 1/а², 1/а³ пишу а^-1, а^-2, а^-3и т.д."

Задание 1. Представьте каждое из этих чисел в виде степени числа 10:

...1000,100,10, 1, 1/10, 1/100,1/1000...

(... 10³, 10², 10¹, 10°, 1/10¹, 1/10², 1/10³...)

Задание 2. Подпишите под этими числами  показатели  степеней:

3, 2, 1, 0,....

Продолжив этот ряд, мы получим числа -1, -2, -3  и  т.д.

Сравним  показатели  соседних степеней.  Показатель  каждой степени на 1 меньше следующего. Распространим этот закон на числа справа от 10°. Получим: 1/10¹ = 10^-1, 1/10² = 10^-2...

Получается такая строка:

10^-3, 10^-2, 10^-1, 10°, 10¹, 10², 10³...

Вопрос. Можем ли мы взять  степень  с другим основанием? С любым?

Ответ. Кроме 0.

Вывод. Итак, мы можем это соглашение распространить на любое число а, отличное от нуля. Запишите в тетради формулу:

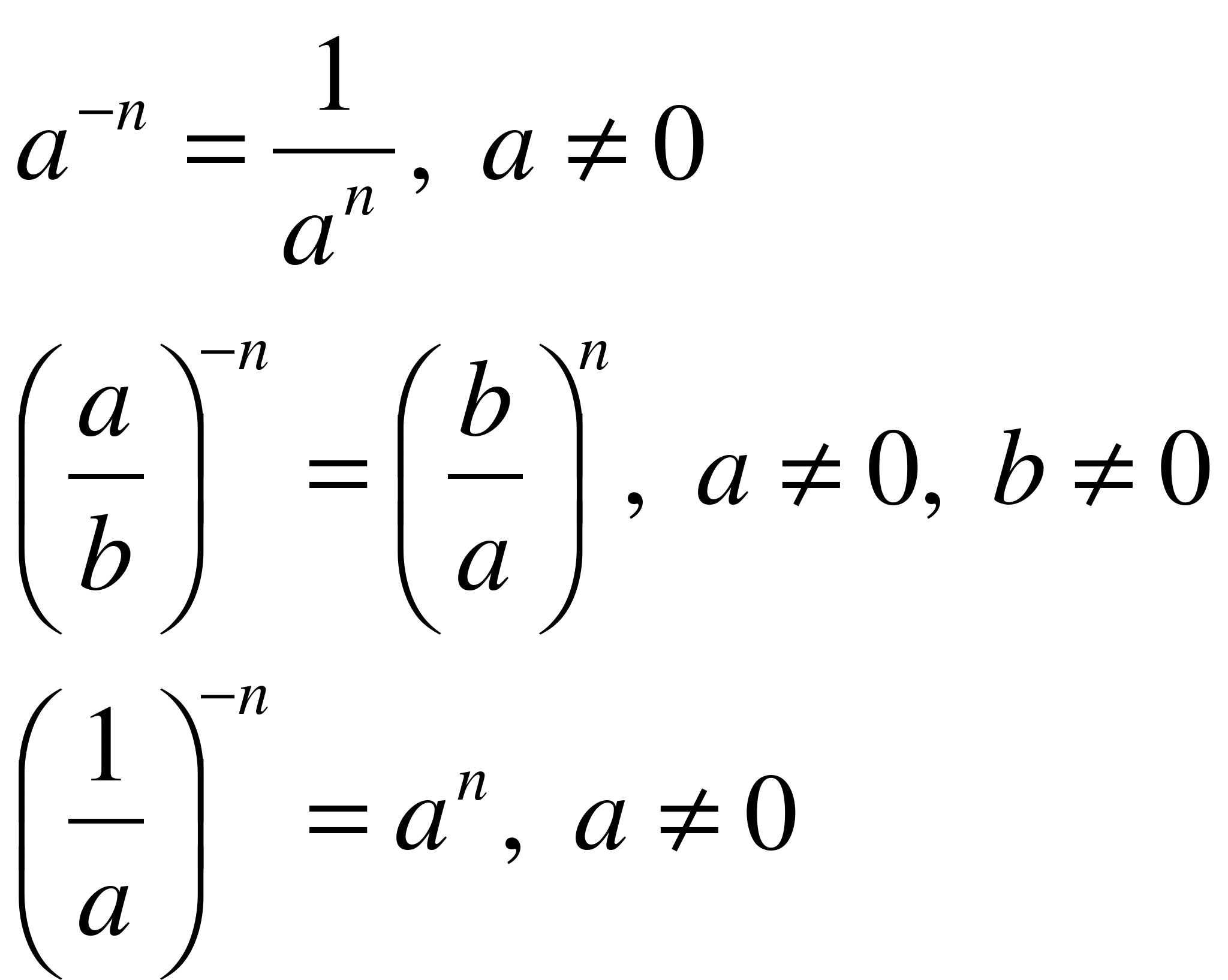
Работа  с учебником

Задание3.. Вычисли значение выражения:

обобщить алгоритм вычисления значений такого типа выражений (содержащих  степень  с отрицательным  показателем ).

1) Выполнить возведение в  степень ;

2) Выполнить действия с дробями;

3) Заменить  степени  с отрицательными  показателями  на  степени   с   натуральными   показателями .

Верная последовательность выполнения шагов:

1. Заменить  степени  с отрицательными  показателями  на  степени   с   натуральными   показателями ;

2. Выполнить возведение в  степень ;

3) Выполнить действия с дробями.

Вопрос. Имеет ли смысл выражение 0^-5?

Ответ. Нет, т.к. основание  степени  с отрицательным  показателем  должно быть отлично от нуля.

Вывод. 0ⁿ имеет смысл только при положительных значениях n.

Группа «Великаны»

Наша система счисления создана индусами. Она была завезена в Европу арабами и потом распространилась по всему миру.

Система названий, принятая почти во всем мире, связана с названием классов.

1 класс – класс единиц.

2 класс – класс тысяч.

3 класс – класс миллионов.

4 класс – класс биллионов или миллиардов.

5 класс – класс триллионов.

6 класс – класс квадриллионов.

7 класс – класс квинтиллионов.

8 класс – класс секстиллионов.

Далее идут септиллион, октиллион, нониллион, дециллион. Конечно, зная такие огромные числа, в этом случае запись числа занимает много места и мало наглядна, неудобно было бы с ними работать . Поэтому решено было изменить написание таких чисел. При записи больших чисел часто используют степень числа 10.

Таким образом,

Тысяча – 1000 = 10³

Миллион – 1000000 - 10⁶

Биллион – 1000000000=10⁹

Триллион - 1000000000000 = 10¹²

Квадриллион – 1000000000000000=10¹⁵

Квинтиллион – 1000000000000000000 = 10¹⁸

Секстиллион – 1000000000000000000000=10²¹

Септиллион – 1000000000000000000000000=10²⁴

Октиллион – 1000000000000000000000000000=10²⁷.

Например, большим числом выражается масса Земли –
5980000000000000000000000 кг.

Давайте с помощью таблицы его прочитаем.

На доске таблица названий больших чисел.

МИЛЛИОН – 6

МИЛЛИАРД – 9

ТРИЛЛИОН – 12

КВАДРИЛЛИОН – 15

КВИНТИЛЛИОН – 18

СЕКСТИЛЛИОН – 21

СЕПТИЛЛИОН – 24

ОКТИЛЛИОН – 27

НОНИЛЛИОН – 30

ДЕЦИЛЛИОН – 33

Величайший числовой гигант скрывается в том воздухе, которым мы дышим. Каждый кубический сантиметр воздуха, каждый наперсток заключает в себе 27 квинтиллионов (т. е. 27 с 18 нулями) мельчайших частиц, называемых «молекулами».

Невозможно даже представить себе, как велико это число. Если бы на свете было столько людей, для них буквально недостало бы места на нашей планете. В самом деле: поверхность земного шара, считая все его материки и океаны,- равна 500 миллионам кв. км. Раздробив  в квадратные метры,  получим 500 000 000 000 000кв.м.

Поделим 27 квинтиллионов на это число, и мы получим 54 000. Это означает, что на каждый квадратный метр земной поверхности приходилось бы более 50 тысяч человек!

Но эти названия почти не используются. Астрономы и физики, имеющие дело с большими числами, предпочитают записывать числа с помощью степени числа десять.

Есть еще одно число – 10¹⁰⁰. Для этого числа придумано специальное название – гугол.

Примеры некоторых числовых великанов.

1). 509 000 000 кв.км – поверхность земного шара.
2). 149 500 000 км – расстояние от Земли до Солнца.
3). 6 000 000 000 000 000 000 000 т – масса земного шара.

Мы с трудом ориентируемся в больших числах, даже миллиона мы как следует себе не представляем.

Каждый из вас умеет складывать, отнимать, умножать и делить числа, которые выражены многими тысячами и даже миллионами.

Как представить себе 1 000 000 учащихся? Трудно? Чтобы это представить, посчитайте, на сколько километров протянулась бы шеренга в 1 000 000 учащихся, если бы каждые 2 из них заняли 1м. Почти от Москвы до Санкт-Петербурга протянулась бы эта шеренга!

Миллион можно назвать карликом по сравнению с таким числом, как миллиард..

Миллиард – это не просто великан, а великанище. Ведь совсем небольшой промежуток времени – 1 минута. А миллиард таких минут – эта более 19 столетий.

Секунда времени в сравнении с часом нам кажется мгновением. Но миллиард секунд – это около 32 лет.
Легенда о шахматной доске.

Шахматы – одна из самых древних игр. Эта игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием. Царь хотел лично наградить изобретателя за удачную выдумку.

Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников. Сета удивил царя беспримерной скромностью своей просьбы. Сета попросил выдать ему за первую клетку шахматной доски одно пшеничное зерно, за вторую клетку – 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32 и т.д.

Царь с раздражением сказал, что эта просьба недостойна его щедрости.

Придворные математики очень долго вели подсчет. Это оказалось чудовищное число: 18 446 744 073 709 551 615 (18 квинтиллионов 446 квадриллионов 744 триллиона 73 биллиона 709 миллионов 551 тысяча 615.

Группа «Стандарты»

Стандарт, это образец эталон, с которого сопоставляется, т. е. когда говорят о стандарте людям легче представить, о чем идет речь.

Стандартный вид числа. В окружающем нас мире мы сталкиваемся с очень большими и с очень маленькими числами. Где вы встречались с такими числами? Если числа очень большие или маленькие удобно ли записывать числа в таком виде? Почему? (занимает много места, времени для записи, сложно запомнить)

Как вы считаете, какой выход нашли из этой ситуации. Записать с помощью степени.

598 000 000 000 000 000

Попробуйте записать это число короче.

598∙10¹⁵, 59,8∙10¹⁶, 5,98∙10¹⁷, 0,598∙10¹⁸

Все результаты верны. Подумайте, посоветуйтесь и выскажите свое мнение, какая же запись может быть стандартной.

5,98∙10¹⁷ –почему?

Мы представили число в виде двух множителей. Первый множитель число принадлежащее промежутку от 1 до 10 «положительный». Второй множитель число 10 в любой  степени  тоже положительно, а при умножении двух положительных чисел получается только положительное число.

-Итак, стандартным видом числа А называется запись вида а∙10ⁿ ,где 1≤ а

n- порядок числа, n-целое.

Группа «Умники»

- Ребята какие же действия можно выполнять с выражениями содержащими степень

Пример 2. Найти значение выражения

при a = - 1, b = 0, c = 1.

9. Итоги урока. Д/з.

Интегрированное домашнее задание

Творческий уровень: составьте математическую шифровку, используя  степень  с  целым  отрицательным  показателем .

10.Рефлексия.