Конспект урока «Пропорция» по математике для 6 класса

Общеобразовательное учреждение

средняя общеобразовательная школа № 11

имени Героя Советского Союза Аипова М.И.

г.Октябрьска Самарской области

Конспект урока по математике
в 6 классе

«Пропорции»

подготовила

учитель математики

Шангина Ирина Евгеньевна

Октябрьск 2011

Шангина Ирина Евгеньевна,

учитель математики

2 категории

ОУ СОШ № 11
г.Октябрьска Самарской области

Урок по математике в 6 классе

Тема: Пропорция.

Цель: закрепить умения и навыки решения задач с помощью пропорций.

Задачи:

• Повторить понятия отношения, пропорции, прямой и обратной пропорциональных зависимостей; закрепить навыки нахождения неизвестного члена пропорции; навыки решения задач с помощью пропорций.

• Способствовать воспитанию интереса к предмету через нетрадиционную форму проведения урока.

• Развивать логическую смекалку, творческое мышление.

Тип урока: урок повторения и закрепления знаний учащихся с использованием ИТ.

Формы организации учебной деятельности: коллективная, индивидуальная.

Оборудование: магнитофон, набор индивидуальных карточек, аудиофайлы с музыкой для физкультминутки.

Ход урока

1. Организационный момент.

• Здравствуйте, ребята. Садитесь, пожалуйста. Мы начинаем наш урок.

• Сегодня в кабинете математики открыт научно-исследовательский институт. Директором НИИ назначили меня, а все учащиеся школы его научные сотрудники. В вашем классе открыта лаборатория № 1, которая сегодня будет заниматься обобщением знаний по теме: «Пропорция».

• Для работы мне понадобятся помощники – старшие научные сотрудники – которые будут помогать мне в течение урока.

• А теперь в ваших журналах наблюдения – рабочих тетрадях – запишем число, классная работа, тема урока: «Пропорция».

2. Устная работа.

• В нашем институте создали необычный цветок. На каждом его лепестке написан вопрос по теме: «Пропорция». С помощью этого цветка я проверю ваши теоретические знания. Вы будите по одному отрывать лепестки и отвечать на вопросы.

1. Что называют отношением двух чисел?

{Частное двух чисел называют отношением этих чисел}

2. Что показывает отношение двух чисел?

{Отношение двух чисел показывает во сколько раз первое число больше второго, или какую часть первое число составляет от второго}

3. Что такое пропорция?

{Равенство двух отношений называют пропорцией}

4. Как называют числа составляющие пропорцию?

{Числа, составляющие пропорцию, называются членами этой пропорции}

5. Назовите средние и крайние члены пропорции 100 : 200 = 4 : 8.

{Числа 100 и 8 – крайние члены пропорции, а числа 200 и 4 – средние члены}

6. Приведите пример пропорции.

{Ответы учащихся}

7. Сформулируйте основное свойство пропорции.

{Произведение крайних членов равно произведению средних членов}

8. Какие величины называют прямо пропорциональными?

{Две величины называются прямо пропорциональными, если с увеличением одной из них в несколько раз другая увеличивается во столько же раз}

9. Какие величины называют обратно пропорциональными?

{ Две величины называются обратно пропорциональными, если с увеличением одной из них в несколько раз другая уменьшается во столько же раз}

• Сотрудник нашего НИИ составил следующие пропорции:

3 : 6 = 2 : 4

8 : 4 = 2 : 3

4 : 6 = 2 : 3

6 : 3 = 2 : 4

3 : 6 = 4 : 2

6 : 4 = 3 : 2

• Все ли из этих пропорций являются верными?

{3 : 6 = 2 : 4 (верная, так как 3 · 4 = 12, 6 · 2 = 12)

8 : 4 = 2 : 3 (неверная, так как 3 · 8 = 24, 4 · 2 = 8)

4 : 6 = 2 : 3 (верная, так как 4 · 3 = 12, 6 · 2 = 12)

6 : 3 = 2 : 4 (неверная, так как 6 · 4 = 24, 3 · 2 = 6)

3 : 6 = 4 : 2 (неверная, так как 3 · 2 = 6, 6 · 4 = 24)

6 : 4 = 3 : 2 (верная, так как 6 · 2 = 12, 4 · 3 = 12)}

3. Письменные задания.

• Вот к нам поступило первое серьезное задание:

«Найдите неизвестный член пропорции:

а) 5,4 : х = 2,7 : 0,1; б) ; в) 4 : 14 = : х»

Решение.

а) 5,4 : х = 2,7 : 0,1 б) в) 4 : 14 = : х

5,4 · 0,1 = х · 2,7 10 · 1,4 = х · 28 4 · х = 14 ·

х · 2,7 = 0,54 х · 28 = 14 4 · х =

х = 0,54 : 2,7 х = 14 : 28 4 · х =

х = 0,2 х = 0,5 х = : 4

Ответ: х = 0,2 Ответ: х = 0,5 х =

Ответ: х =

• Все НИИ решают задачи, которые потом применяются на практике. И у нас, в середине рабочего дня, практические задания.

Задача 1. На изготовление 8 деталей требуется грамм серебра. Сколько серебра потребуется на изготовление 12 таких деталей?

Решение.

1. О зависимости каких величин идет речь в задаче? (количество и масса)

2. Какая это зависимость? (прямо пропорциональная)

3. Составим краткую запись по условию задачи.

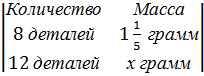
4. Составим пропорцию по условию задачи.

8 : 12 = : х

х · 8 = 12 ·

х · 8 =

х · 8 =

х = : 8

х =

5. Запишем ответ.

Ответ: для изготовления 12 деталей потребуется грамм серебра.

Задача 2. Чтобы вывезти товар, прибывший на железнодорожную станцию, потребуется 21 автомашина грузоподъемностью 2,5 т. Сколько потребовалось бы автомашин грузоподъемностью 3,5 т.

Решение.

1. О зависимости каких величин идет речь в задаче? (количество и грузоподъемность)

2. Какая это зависимость? (обратно пропорциональная)

3. Составим краткую запись по условию задачи.

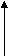
4. Составим пропорцию по условию задачи.

21 : х = 3,5 : 2,5

х · 3,5 = 2,5 · 21

х · 3,5 = 52,5

х = 52,5 : 3,5

х = 15

5. Запишем ответ.

Ответ: для вывоза товара потребуется 15 автомашин.

4. Физкультминутка.

• Как и у каждого учреждения у нас перерыв (физкультминутка).

• Чтобы перерыв был полезным его проведет старший научный сотрудник.

Звучит музыка.

Быстро встали, улыбнулись.

Выше-выше потянулись.

Ну-ка, плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали. Сели, встали.

И на месте побежали.

• Молодцы. Перерыв закончен. Садитесь.

5. Тестовая работа.

• Пока вы отдыхали, я узнала, что руководство НИИ решило провести тестирование научных сотрудников. Вот сейчас этим мы и займемся.

• Перед вами лежат бланки с тестами. Подпишите их. В этом тестовом задании вам нужно выбрать правильный вариант ответа и обвести его кружочком.

• Все готовы? Тогда начинаем.

Фамилия, имя _________________________

Класс 6 «А»

Вариант 1

1. Выразите отношение 96 : 64 в процентах.

А) 150 %

Б) 125 %

В) 120 %

Г) 105 %

2. Найдите отношение 20 минут к 2 часам.

А) 1 : 6

Б) 10 : 1

В) 1 : 10

Г) 6 : 1

3. Какое выражение подходит для вычисления неизвестного члена пропорции х : 1,6 = 3 : 5?

А) Б)

В) Г)

4. Найдите неизвестный член пропорции 3 : 8 = х : 3,2

А) 1,2

Б) 2,4

В) 0,6

Г) 0,12

5. Дана пропорция 10 : а = 20 : с. Какое из следующих равенств пропорцией не является?

А) а : с = 10 : 20

Б) а : с = 20 : 10

В) с : а = 20 : 10

Г) а : 10 = с : 20

• Время закончилось. Я попрошу старших научных сотрудников собрать бланки с тестами.

6. Исторические сведения.

• В конце рабочего дня наши научные сотрудники решили рассказать о применении пропорции в жизни человека.

Золотое сечение в архитектуре.

Различают архитектурные пропорции и пропорции, используемые для изображения человеческого тела и лица. Самые простые пропорции основаны на кратких и целочисленных отношениях, например 1:2, 3:4 и т.д. Но уже с древности широко распространились системы пропорционирования, приводящие к иррациональным отношениям. Самым популярным из них является золотое сечение.

Идея золотого сечения принадлежит греческим ученым. Золотое сечение - это выражение совершенной пропорции. Греки использовали этот принцип в архитектуре. Это означает соблюдение определенных соотношений между размерами отдельных частей здания. Одним их красивейших произведений древнегреческой архитектуры является Парфенон (V век до н.э.). Отношение высоты здания к его длине равна 0,618.

Другим примером из архитектуры древности является Пантеон. Из всех древних зданий наилучшим образом сохранился Пантеон. Он до сих пор поражает воображение. Здание украшено цветным мрамором. До сих пор Пантеон остается действующим храмом, здесь располагается христианская церковь.

Примером использования золотого сечения в архитектуре также является Покровский собор (собор Василия Блаженного). Он был построен в честь взятия русскими войсками Казани в 16 веке. Этот удивительный по своей красоте храм строили русские мастера Барма и Постник.

Храм Покрова Богородицы на Нерли был построен в 1165 году, посвящен новому празднику на Руси - Покрова Богородицы. Пропорции и простота этого храма делают его светлым, легким, невесомым.

Золотое сечение в скульптуре.

Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции золотого сечения создают впечатление гармонии, красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении золотого сечения. Так, например, знаменитая статуя Апполона Бельведерского состоит из частей, делящихся по золотым отношениям. Великий древнегреческий скульптор Фидий часто использовал золотое сечение в своих произведениях. Самым знаменитым из них была статуя Зевса Олимпийского (одно из чудес света).

Для взрослых мужчин отношения размеров тела равны 0.615, а для женщин 0.6, так что пропорции мужчин ближе к золотому сечению, чем пропорции женщин.

Золотое сечение в живописи.

Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно притягивающие наше внимание, так называемые зрительные центры. Таких точек всего 4 и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости. Это «золотое сечение» картины. Чтобы привлечь внимание к главному элементу фотографии, надо совместить этот элемент с одним из зрительных центров.

Примером использования золотого сечения в живописи наиболее просматриваются в картинах И.И. Шишкина. Это «Корабельная роща», «На севере диком», «Утро в сосновом лесу».

Холст, на котором написана картина «Тайная вечеря» Сальвадора Дали, имеет форму золотого прямоугольника. Он использовался для создания у зрителей ощущения покоя, уравновешенности.

Примером использования золотой спирали в живописи является картина «Избиение младенцев» Рафаэля. Золотая спираль применялась для выражения тревоги, бурных событий.

Золотое сечение в картине Леонардо да Винчи «Джоконда». Портрет Моны Лизы привлекает тем, что композиция рисунка построена на «золотых треугольниках» (треугольниках, являющихся кусочками правильного звездчатого пятиугольника).

Золотое сечение в природе.

Даже сама природа подчиняется закону «Золотого сечения». Если рассмотреть расположение листьев на общем стебле растений, можно заметить. Что между каждыми двумя парами листьев (А и В) третья расположена в месте золотого сечения (точка В). Золотую спираль в природе представляют раковины многих молюссков. Рога архаров закручиваются по золотой спирали. Паук эпейра сплетает паутину по золотой спирали. Спиралью закручивается ураган. Семечки в корзине подсолнуха выстраиваются по спирали, а также чешуйки сосновых шишек и ячейки ананасов. В ящерице с первого взгляда улавливаются приятные для глаз пропорции - длина ее хвоста так относится к длине остального тела, как 62 к 38.

7. Итог урока.

• Ну а теперь подведем итог урока.

• Так как сегодня вы были в роли научных сотрудников НИИ, то домашнее задание у вас будет творческим. Дома вам нужно будет составить 2 задачи на прямую и обратную пропорциональные зависимости.

• На ваших рабочих столах лежат кружки, изображающие различное настроение:

• У меня от урока вот такое настроение. А у вас?

Ребята поднимают кружочки.

• А теперь приклейте эти кружочки в свою тетрадь.

• На этом наш урок закончен.

• Спасибо за работу.

Использованные источники:

http://www.abc-people.com/idea/zolotsech/

http://goldsech.narod.ru/

http://arx.novosibdom.ru/node/419

http://festival.1september.ru/articles/532746/

"Математика": Приложение к газете “1 сентября”, 42/2000г., Егупова М., Павленкова И. “Экология и планиметрия”.