Классный час «Жизнь твоя на стекло нанесенный рисунок» по математике для 11 класса

МО классных руководителей

МБОУ СОШ № 7

города Смоленска

Классный час

«Жизнь твоя на стекло нанесенный рисунок»

Классный руководитель

11 А класса

Байрамова Елена Николаевна

2008 – 2009 учебный год

Классный час

«Жизнь твоя на стекло нанесенный рисунок»

ЦЕЛЬ:

предоставить возможность старшеклассникам выразить свое отношение к жизни и творчеству великого Омара Хайяма.

ЗАДАЧИ:

• познакомить учащихся с путями формирования алгебры на Арабском Востоке и в Средней Азии;

• помочь старшеклассникам понять, как из разрозненных фактов создаются общие математические идеи;

• описать жизненный путь научного гения своей эпохи – великого Омара Хайяма;

• продолжить развивать навыки дискуссии и творчества (коммуникативные компетенции);

• продолжить воспитывать интерес к литературе, на примерах знакомства с великими произведениями мировой литературы, погрузиться в «Сад поэзии» поэта.

ФОРМА: творческая мастерская.

ОБОРУДОВАНИЕ:

портрет Омара Хайяма, коллаж из книг, альбомов, статей о жизни и творчестве Омара Хайяма; раздаточный материал (листы цветной бумаги формата А4, траектория классного часа); презентация «Жизни твоя на стекло нанесенный рисунок»; веточки цветущих деревьев.

ВРЕМЯ: 2 часа.

Предварительное домашнее задание

• Задачи Омара Хайяма

1. Решите уравнение .

2. Упростите систему уравнений: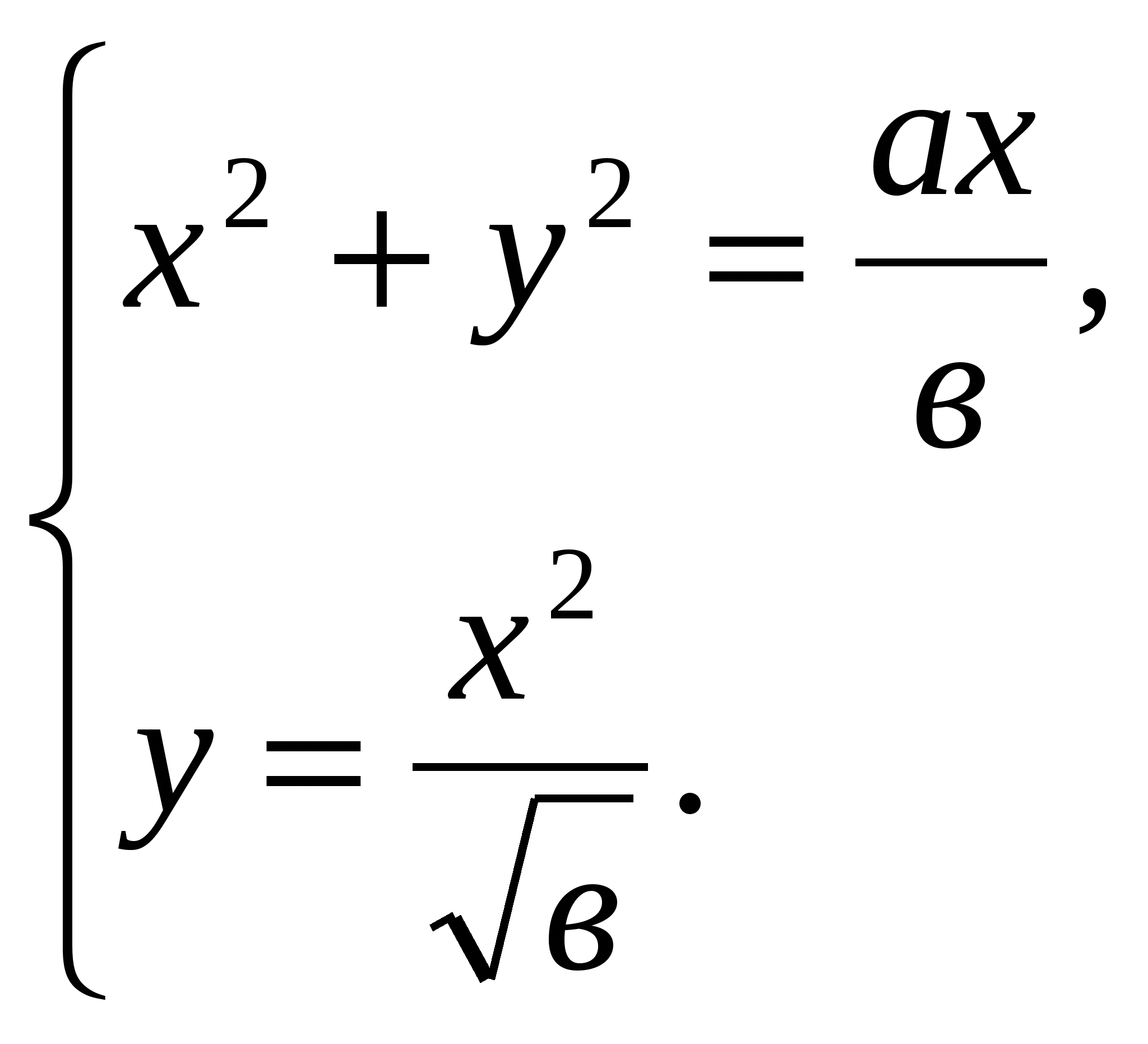

• Подготовить ответы

Эпоха конца XI - начало XII века (Арабский Восток и Средняя Азия)

Что такое рубаи?

Что в творчестве О. Хайяма означает «вино», «глина», «роза»?

Ваши любимые рубаи.

Для чего мы живем? Как живем? Куда и зачем стремимся?

Ход классного часа

1. Индуктор.

Учитель медленно читает четверостишие Омара Хайяма:

От безбожия до Бога – мгновенье одно,

От нуля до итога – мгновенье одно.

Береги драгоценное это мгновенье.

Жизнь – ни мало, ни много – мгновенье одно.

Выберите самое значимое для вас слово или выражение и запишите на своем листе бумаги.

2. Погружение в эпоху конца XI - начало XII века – время жизни и творчества О. Хайяма.

Учитель просит выразить одним словом или словосочетанием, кем был Омар Хайям (на доске в ходе обсуждения появляются записи).

Историческая справка:

Ведущую роль в развитии математики в средние века играли ученые стран Востока. В VII веке мир был поражен необыкновенно быстрым возвышением Арабской империи. Меньше, чем за 100 лет арабы овладели огромной территорией. Они завоевали Сирию, Иран, Египет, захватили Хорезм и часть Пенджаба. В Арабский Халифат в середине VIII века входили Пиренейский полуостров, все средиземноморские страны Африки, Ближний Восток, большие районы Малой Азии, Кавказа и Средней Азии, часть долины Инда.

Завоевания проводились под знаменем новой религии – ислама. Язык этой религии, арабский, стал государственным, и основным научным языком. Математические открытия были результатом сотрудничества ученых многих народов – персов, арабов, таджиков, сирийцев и других, но используются термины: «арабская математика», «математика стран ислама».

Рассвет культуры и науки стран ислама приходится на VII – XV века. Сохранилось предание о том, что халиф Омар, завоевав Александрию, приказал уничтожить ее знаменитую библиотеку. Он сказал: «Если в книгах содержится нечто, ведущее к истине, то мы имеем от Аллаха то, что еще лучше ведет к ней, а если в ней содержится ложное, то они не нужны». Эти слова отражают фанатизм первых арабских завоевателей.

Последующие правители содействовали процветанию наук. Жизненно важными в Арабском Халифате были вопросы орошения, строительства, караванной и морской торговли. Для их решения требовалось развитие астрономии и математики.

Преуспевающие правители создавали обсерватории, которые становились центрами развития точных наук. В них изучались, переводились на арабский язык и комментировались труды ученых Индии и Древней Греции.

Первым научным центром халифата был Багдад. В конце VIII века в нем собрано много ученых и переводчиков из разных стран.

Халиф Гарун ал-Рашид, правивший с 786 по 809 г, известный (правда в очень идеализированном виде) по сказкам «Тысячи и одной ночи», содействовал развитию естественных наук и математики. При нем была открыта большая библиотека, которая пополнялась рукописями даже из Византии. В городе имелись десятки других библиотек и множество людей было занято переводами научных сочинений.

Халиф ал-Мамун, сын Гаруна ал-Рашида, объединил ученых в своего рода академии, названной «Домом мудрости». При «Доме мудрости» имелась хорошо оборудованная обсерватория. Были выполнены обширные работы по астрономии и географии. Большой интерес правителей вызывала астрология, и поэтому развитию астрономии на Востоке уделялось много внимания.

В Багдадской математической школе большое место занимало изучение и издание по-арабски древних авторов. Были переведены с греческого на арабский основные произведения Евклида, Архимеда, Апполония, Менелая, Герона, Птоломея, Диофанта и других авторов. Сочинения греческих авторов стали настольными руководствами арабских ученых.

Математика стран ислама включала в себя также знания, полученные в Индии, Вавилона, Персии, Хорезма. Позднее приобрели значение научные связи с Китаем, хотя прямых переводов с китайского на арабский, насколько известно, не было.

Замечательных результатов добились ученые стран ислама в изучении уравнений третьей и частично четвертой степени.

Арабские ученые использовали методы, разработанные в Древней Греции: метод вставок, метод конических сечений и другие.

Античная наука обращалась к кубическим уравнениям лишь эпизодически. На арабском Востоке над этой проблемой работали многие математики, в результате его был накоплен большой материал. Возникла необходимость в его систематизации, в построении общей теории.

3. Сад математики великого математика

Это сделал Омар Хайям (1048 – 1131) – выдающийся математик, астроном, философ и поэт, широко известный в наши дни как автор знаменитых четверостиший.

Он родился в городе Нишапуре (север Ирана) в области Хорасан, жил и работал в Самарканде, Бухаре и других городах Средней Азии и Ирана. В трудное время политических неурядиц, воин, страшных разрушений и массовых убийств жизнь ученого была очень тяжела. Хайям испытывал нужду, страдал из-за религиозных преследований. Лишь изредка он имел возможность спокойно заниматься наукой. Так некоторое время ему покровительствовал богатый вельможа Абу-Тахир, предположительно главный судья Самарканда, и Омар Хайям написал замечательный алгебраический трактат «О доказательствах задач алгебры и алмукабалы», посвященный решению кубических уравнений. В этом трактате Хайям писал: «Мы были свидетелями гибели ученых, от которых осталась малочисленная, но многострадальная кучка людей».

Когда Хайям был молодым, Среднюю Азию и Иран завоевали кочевник турки – сельджуки. В 1074 г. Ученый был приглашен в столицу сельджуков Исфахан (Иран) для работы в астрономической обсерватории, где ему оказали покровительство визирь Низам ал-Мулк и султан Маликшах.

Хайям стал главой обсерватории. Он работал над реформой иранского солнечного календаря, проводил астрономические наблюдения, составил «Маликшахские астрономические таблицы», написал выдающийся математический трактат «Комментарии к трудным постулатам книги Евклида».

Параллельно с занятиями наукой Хайям создавал свои четверостишия («Рубаи»). Научные труды Хайям писал на арабском языке, стихотворения на персидско-таджикском наречии.

В 1092 году был убит Низам ал-Мулк и умер Маликшах. Реформа календаря не осуществилась. Была закрыта обсерватория. Хайям, который в своих стихах высмеивал догмы официальной религии, был обвинен в безбожии. На старости лет он вынужден был совершить паломничество в Мекку. Хайям скончался в бедности в родном Нишапуре.

В трудах персидского математика ал-Караджи были изучены уравнения, квадратные относительно xⁿ, исследованы многие неопределенные уравнения, например, , составлена таблица для (а + в)ⁿ до n = 12.

В трактате «Трудности арифметики» Омар Хайям, по-видимому, нашел общую формулу для возведения бинома (а + в) в степень n. Однако этот трактат утерян. Первые дошедшие до нас сочинение, в котором содержится общая формула для (а + в)ⁿ , n – любое натуральное число, принадлежит Насир ад-Дину ат-Туси (1265 г.).

Хайям развил геометрическую теорию кубических уравнений. В своем алгебраическом трактате он высказал мысль о том, что уравнения третьей степени нельзя решить с помощью циркуля и линейки. Хайям подчеркнул, что их решение «может быть, произведено только при помощи конических сечений».

Хайям рассматривал уравнения с произвольными положительными коэффициентами и разыскивал положительные корни. Он дал классификацию кубических уравнений, выделив 19 классов, из которых 5 классов сводится к линейным или квадратным (dx³ = cx², dx³ = bx и другие) Для каждого из остальных 14 классов (dx³ = a; dx³ +bx = a и так далее) Хайям указал метод решения с помощью конических сечений: парабол, равносторонних гипербол и окружностей.

Как и все математики Востока, Хайям описывал уравнения словесно. Так фраза «Куб и корни равны числу» у него означает уравнение х³ + bx = a. Чтобы его решить, Хайям рассмотрел окружность и параболу .

Абсцисса точки пересечения кривых, которая не совпадает с началом координат, есть корень данного уравнения. Действительно, можно записать систему: 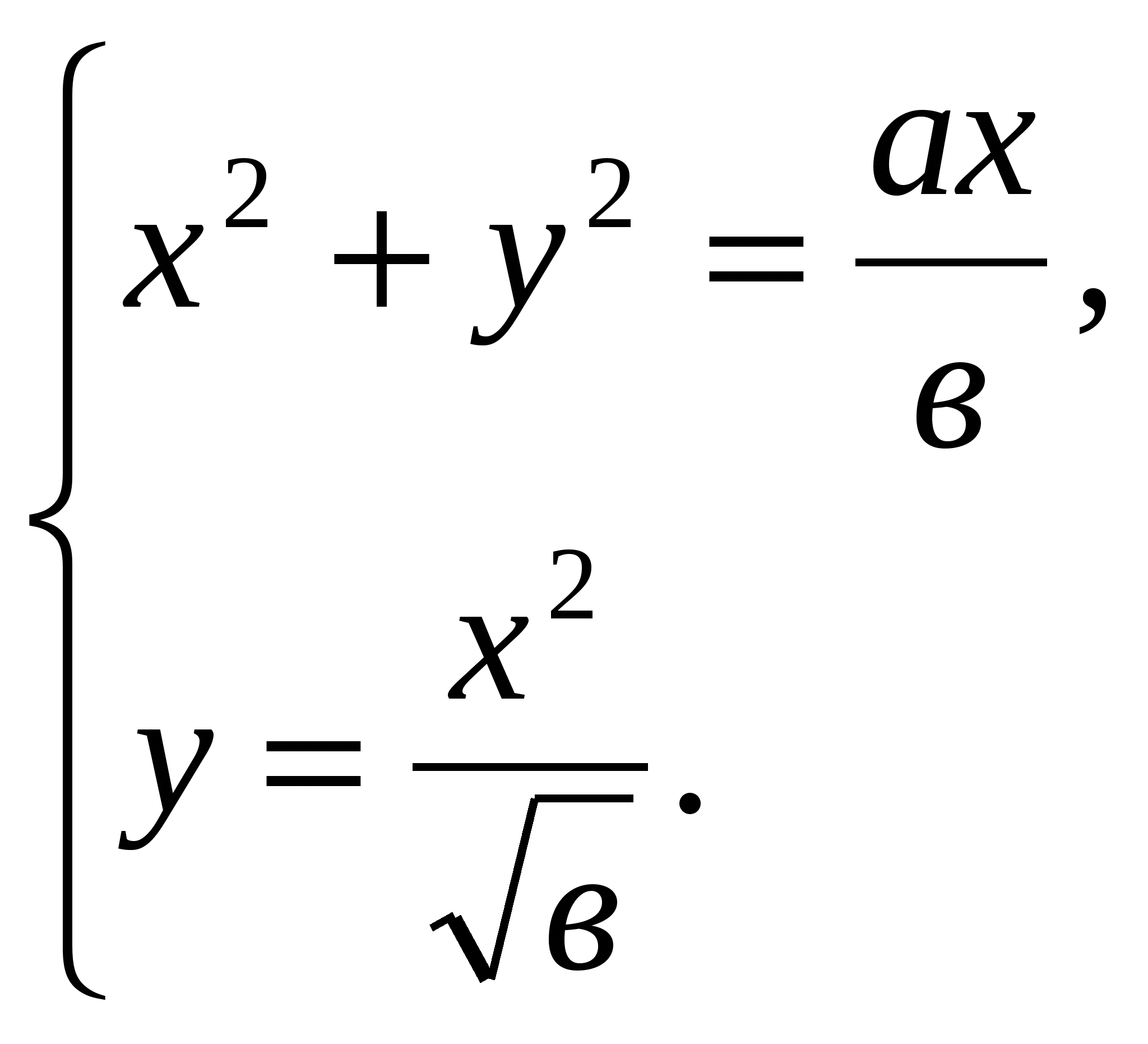Отсюда при получаем , .

Для каждого из 14 классов Хайям решал вопрос о числе положительных корней в зависимости от условий, накладываемых на коэффициенты уравнений. Так он указал, что уравнение х³ + bx = a всегда имеет единственный положительный корень. Лишь рассматривая класс уравнений х³ + вх = сх² + а, Хайям допустил неточность, не заметив, что оно может иметь три положительных корня. Эту возможность открыл в XVI веке Дж. Кардано.

Хайям поставил проблему решения кубических уравнений в радикалах с помощью алгебраической формулы, но не сумел решить ее и написал: «Может быть, кто-нибудь из тех, кто придет после нас, узнает это».

Формулы для решения кубических уравнений нашли в XVI веке итальянские математики Ш. дель Ферро и Н. Тарталья, а опубликовал Кардано в 1545 г.

Омар Хайям навсегда вошел в историю всемирной культуры не только как блестящий ученый энциклопедист, но и как прекрасный поэт, который воспевал свободу, бичевал ханжество и лицемерие, высмеивал суеверия. Его мудрые лирические четверостишия, наполненные глубоким философским смыслом, в XIX и XX веках были переведены на все основные языки мира.

На могиле Омара Хайяма в Нишапуре в 1934 г. Воздвигнут обелиск.

Вот одно из четверостиший Хайяма:

Чтоб мудро жизнь прожить, знать надобно немало.

Два важных правила запомни для начала.

Ты лучше голодай чем, что попало есть,

И лучше будь один, чем вместе с кем попало.

4. Работа в группах.

Каждой группе выдается портрет Омара Хайяма.

- Рассмотрите портрет Омара Хайяма. Что можно сказать об этом человеке?

В ходе обсуждения портрета учащиеся дополняют свои записи – список характеристик.

Каждой группе выдаются карточки с описанием жизни и творчества О. Хайяма.

- Всмотритесь вновь в портрет поэта, философа, ученого, человека. Вчитайтесь, вслушайтесь в те строчки, которые Вам даны на карточке. Произнесите их в слух и дополните ваши записи тем, что показалось вам особенно важным.

- Ваши первые впечатления об ученом, поэте, философе, мудреце, человеке.

Содержание карточек:

Ученый. «Не было ему равного в астрономии и философии. О, если бы ему была дарована способность, избегать неповиновения Богу»

Писатель Садек Хедаят писал: «Пожалуй, во всем мире не найти книг, подобных сборнику стихов Омара Хайяма, расхваленному, преданному анафеме и ненавидимому, искаженному и оклеветанному, подвергнутому скрупулезному толкованию, приобретшему всеобщую славу, завоевавшему весь мир и в конечном счете так и не познанному»

Математик. «Своими математическими исследованиями он обогатил современную ему математику Запада на 500 лет»

Астроном. «Он разработал самый точный в мире календарь, который на 7 секунд точнее современного»

Он написал трактаты по философии, физике, математической теории, музыке, поэзии.

«Очень жаль – писал историк, - что никто из знающих математику не имеет вкуса к арабской литературе, а никто из знающих арабскую литературу не имеет вкуса к математике. По этой причине математические открытия Омара Хайяма остались неизвестными европейским ученым»

Поэзия Хайяма – это Сад Хайяма. У него есть начало и не будет конца.

Хайям не только великолепно на память знал Коран, но мог дать толкование любого айята (стиха) этой главной книге мусульман.

Омар Хайям родился в Хорасане, в древнем городе Нишапуре, в семье ремесленника, быть может, старейшины цеха ткачей, изготовлявшего ткани для шатров и палаток. Очевидно, ремесло его предков было почетным, ибо Хайям – псевдоним поэта – происходит от слова «хайма» (шатер, палатка)

Предание говорит, что правитель Бухары, беседуя с Хайямом, «сажал его с собой рядом на престол в знак наивысшего уважения».

Легенда свидетельствует, что Низам ал-Мульк предложил Хайяму управлять городом Нишапур и всей прилегающей областью. Хайям ответил: «Не хочу управлять людьми, приказывать и запрещать!» И тогда Низам ал-Мульк якобы назначил Хайяму годовое жалованье 10000 динаров, дабы он беспрепятственно мог заниматься наукой.

Первые труды молодого Хайяма «Трудные вопросы арифметики» и «Объяснение трудного в заключениях Евклида» прославили его.

Известный исследователь творчества Хайяма индийский ученый Свали Говинда Тиртха вычислил по сочетанию светил в гороскопе, что Хайям родился 18 мая 1048 года.

V. Сад поэзии великого поэта. (работа в группах)

Что такое рубаи? Обсуждение

Рубаи – это стихотворение, обычно афористичное, в котором рифмуются 1,

2, 4-я строчки, иногда все 4 строчки.

Рубаи – величавое эпическое сказание о сложном и трудном, многострадальном и радостном пути человека.

Чтение четверостиший Омара Хайяма. Группа получает стихотворные тексты.

Задание учащимся – определить тему (идею) четверостиший. Несколько выбрать для чтения вслух.

Тексты, предлагаемые для работы в группах (Их классификация известна только учителю).

Познание

Много лет размышлял я над жизнью земной.

Непонятного нет для меня под луной.

Мне известно, что мне ничего не известно! –

Вот последняя правда, открытая мной.

Дураки мудрецом почитают меня.

Видит Бог: я не тот, кем считают меня.

О себе и о мире я знаю не больше

Тех глупцов, что усердно читают меня.

Даже самые светлые в мире умы

Не смогли разогнать окружающей тьмы.

Рассказали нам несколько сказочек на ночь

И отправились, мудрые, спать, как и мы.

Те, что веруют слепо, - пути не найдут.

Тех, кто мыслит, - сомнения вечно гнетут.

Опасаюсь, что голос раздастся однажды:

«О, невежды! Дорога не там и не тут!»

Жизнелюбие

Если б я властелином судьбы своей стал –

Я бы всю ее заново перелистал.

И, безжалостно вычеркнул скорбные строки,

Головою от радости небо достал!

Плеч не горби, Хайям! Не удастся и впредь

Черной скорби душою твоей овладеть,

До могилы глаза твои с радостью будут

На ручей, на зеленую ниву глядеть.

Не оплакивай, смертный, вчерашних потерь,

Дней сегодняшних завтрашней меркой не мерь,

Ни былой, ни грядущей минуте не верь,

Верь минуте текущей – будь счастлив теперь!

Любовь

Прошлась ты по душе, как благодать. Ты кто?

И, сам не свой, прошу: пройди опять! Ты кто?

Ах, ради Бога … Нет, скорее, ради сердца,

Присядь со мной, а я начну гадать: ты кто?

Как ветер, к локонам ее прильну? Едва ль.

Скачу я к пропасти, но поверну едва ль.

На то и зрячи мы, чтоб лица милых видеть …

Я вроде зряч, но ей в лицо взгляну едва ль.

Какой соблазн, какой искус, храни Аллах!..

Твое лицо и день и ночь царит в мечтах.

Вот потому и боль в груди, и трепет в сердце,

И сухость губ, и влажность глаз, и дрожь в руках.

Разлукой сил лишишь, больным и стану я.

Надеждой опьянишь, хмельным и стану я.

Тебе ли спрашивать, каким предстану я?

О ком ты грезила, таким и стану я.

Жизнь и смерть, рок

Я познание сделал своим ремеслом,

Я знаком с высшей правдой и с низменным злом.

Все тугие узлы я распутал на свете,

Кроме смерти, завязанной мертвым узлом.

Тот усердствует слишком, кричит: «Это – я!»

В кошельке золотишком бренчит: «Это – я!»

Но едва успевает наладить делишки –

Смерть в окно к хвастунишке стучит: «Это – я!»

Управляется мир Четырьмя и Семью.

Раб магических чисел – смеряюсь и пью.

Все равно семь планет и четыре стихии

В грош не ставят свободную волю мою!

Слышал я: под ударами гончара

Глина тайны свои выдавать начала.

Но топчи меня! – глина ему говорила. –

Я сама человеком была лишь вчера.

Чтение и обсуждение выбранных четверостиший. По ходу обсуждения на доске записываются слова или выражения, которые характеризуют содержание творчества Омара Хайяма.

- собранные воедино стихи Омара Хайяма звучат, как величавое сказание.

О чем это сказание?

Счастье Добро Жизнь Любовь Путь человека Смерть Роза

Человечность Мысль Свобода Истина Воля Вечность Судьба

Разум Луноликая (возлюбленная) Старость Чаша жизни Низменное зло

Прочитайте эти рубаи. О чем они?

Да пребудет со мною любовь и вино!

Будь что будет: безумье, позор – все равно!

Чему быть суждено – неминуемо будет,

Но не больше того, чему быть суждено.

Пей с достойным, который тебя не глупей.

Или пей с луноликой любимой своей.

Никому не рассказывай, сколько ты выпил.

Пей с умом. Пей с разбором. Умеренно пей.

Если я напиваюсь и падаю с ног –

Это Богу служение, а не порок.

Не могу же нарушить я замысел Божий,

Если пьяницей быть предназначил мне Бог!

«Брось вино! Попадешь, - мне пророчат, - в беду:

В день Суда испекут тебя черти в аду!»

Это так. Но не лучше ли вечного рая

Миг божественной истины в пьяном бреду?

Что скажите? О каком вине писал Омар Хайям? Обсуждение.

Вино, луноликая, роза, глина – все это часто образы, призванные для выражения философских взглядов поэта.

По мнению большинства исследователей, вино в поэзии Хайяма – всего лишь образ, символизирующий свободного от обрядов веры человека, своеобразное отрицание устоев ислама.

И действительно, ислам запрещает пить вино, поэт, напротив, призывает его пить. Но есть и еще корни «винных» рубаи. Хайям, как считают, вел весьма умеренный образ жизни. И к вину подходил в первую очередь как ученый, о чем свидетельствует его трактат о вине. В трактате классифицируются сорта винограда и виноградных вин и приводятся сведения о применении вин для лечения разных болезней.

Глина в поэзии Хайяма означает начало и конец всего сущего, она – символ изменяющейся вечной материи, она материал, из которого «вылеплено» все сущее, стало быть, и шах, и нищий вылеплены из одной глины, а значит, и тот, и другой должны иметь равные права под солнцем.

Роза Хайяма – особенная. Она – то образ цветущей земной жизни, то образ цветущей и увядающей женщины, то символ бренности и краткости человеческого бытия.

VI. Рефлексия.

Для чего мы живем? Как живем? Куда и зачем стремимся?

Может быть, эти рубаи помогут найти ответы.

Учащиеся читают рубаи вслух, выписывают строки о жизни.

Тексты предлагаемые для обсуждения в группах:

Жизни стыдно за тех, кто сидит и скорбит,

Кто не помнит утех, не прощает обид.

Пой, покуда у чанга не лопнули струны!

Пой, покуда об камень сосуд не разбит!

Если жизнь твоя нынче, как чаша, полна – Не спеши отказаться от чаши вина. Все богатство судьба тебе дарит сегодня – Завтра, может случиться, ударит она!
Книга жизни моей перелистана – жаль! От весны, от веселья осталась печаль. Юность – птица: не помню, когда прилетела И когда унеслась, легкокрылая, вдаль.	Мастер, шьющий палатки из шелка ума, И тебя не минует внезапная тьма. О Хайям! Оборвется непрочная нитка, Жизнь твоя на толкучке пойдет задарма.
Жизнь пустыня, по ней мы бредем нагишом. Смертный, полной гордыни, ты просто смешон! Да, для каждого шага находишь причину – Между тем он давно в небесах предрешен	Если жизнь все равно неизбежно пройдет – Так пускай хоть она безмятежно пройдет! Жизнь тебя, если будешь веселым, утешит. Если будешь рыдать – безуспешно пройдет.
В книге судеб ни слово нельзя изменить, Тех, кто вечно страдает, нельзя изменить. Можешь пить свою желчь до скончания жизни. Жизнь нельзя сократить и нельзя удлинить.	Эта жизнь – солончак. Вкус у жизни такой. Что сердца наполняются смертной тоской. Счастлив тот, кто ее поскорее покинет. Кто совсем не родился – познает покой.
От судьбы мне всегда достаются плевки, Жизнь слагается воле моей вопреки. И душа собирается тело покинуть: «Больно стены жилья, говорит – не крепки!»	Хорошо, если платье твое без прорех. И о хлебе насущьном подумать не грех. И всего остального и даром не надо – Жизнь дороже богатства и почестей всех.
Жизнь моя тяжела: в беспорядке дела. Ни покоя в душе, ни двора, ни кола. Только горестей вдоволь судьба мне дала. Что ж, Хайям, хоть за это Аллаху хвала!

Какие чувства вы испытали в процессе работы? Оцените свое состояние.

Учитель заключает: Ученейший муж века; Доказательство истины; Знаток греческой науки; Царь философов Востока и Запада» - таков далеко не полный почетный титул Омара Хайяма.

Омар Хайям завещал: «Меня похоронить в таком месте, где всегда в дни весеннего равноденствия свежий ветер будет осыпать цветами плодовых деревьев». Он похоронен в Нишапуре (Иран). Его полное имя: Гийяс-ад Дин-Абу-л-ф-Фатх ибн Хайям ан-Нишапур.

Этот мир – эти горы, долины, моря –

Как волшебный фонарь. Словно лампа – заря.

Жизнь твоя – на стекло нанесенный рисунок.

Неподвижно застывший внутри фонаря.

ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ

Алгебра на Арабском Востоке и в Средней Азии

Ведущую роль в развитии математики в средние века играли ученые стран Востока. В VII веке мир был поражен необыкновенно быстрым возвышением Арабской империи. Меньше, чем за 100 лет арабы овладели огромной территорией. Они завоевали Сирию, Иран, Египет, захватили Хорезм и часть Пенджаба. В Арабский Халифат в середине VIII века входили Пиренейский полуостров, все средиземноморские страны Африки, Ближний Восток, большие районы Малой Азии, Кавказа и Средней Азии, часть долины Инда.

Завоевания проводились под знаменем новой религии – ислама. Язык этой религии, арабский, стал государственным, и основным научным языком. Математические открытия были результатом сотрудничества ученых многих народов – персов, арабов, таджиков, сирийцев и других, но используются термины: «арабская математика», «математика стран ислама».

Рассвет культуры и науки стран ислама приходится на VII – XV века. Сохранилось предание о том, что халиф Омар, завоевав Александрию, приказал уничтожить ее знаменитую библиотеку. Он сказал: «Если в книгах содержится нечто, ведущее к истине, то мы имеем от Аллаха то, что еще лучше ведет к ней, а если в ней содержится ложное, то они не нужны». Эти слова отражают фанатизм первых арабских завоевателей.

Последующие правители содействовали процветанию наук. Жизненно важными в Арабском Халифате были вопросы орошения, строительства, караванной и морской торговли. Для их решения требовалось развитие астрономии и математики.

Преуспевающие правители создавали обсерватории, которые становились центрами развития точных наук. В них изучались, переводились на арабский язык и комментировались труды ученых Индии и Древней Греции.

Первым научным центром халифата был Багдад. В конце VIII века в нем собрано много ученых и переводчиков из разных стран.

Халиф Гарун ал-Рашид, правивший с 786 по 809 г, известный (правда в очень идеализированном виде) по сказкам «Тысячи и одной ночи», содействовал развитию естественных наук и математики. При нем была открыта большая библиотека, которая пополнялась рукописями даже из Византии. В городе имелись десятки других библиотек и множество людей было занято переводами научных сочинений.

Халиф ал-Мамун, сын Гаруна ал-Рашида, объединил ученых в своего рода академии, названной «Домом мудрости». При «Доме мудрости» имелась хорошо оборудованная обсерватория. Были выполнены обширные работы по астрономии и географии. Большой интерес правителей вызывала астрология, и поэтому развитию астрономии на Востоке уделялось много внимания.

В Багдадской математической школе большое место занимало изучение и издание по-арабски древних авторов. Были переведены с греческого на арабский основные произведения Евклида, Архимеда, Апполония, Менелая, Герона, Птоломея, Диофанта и других авторов. Сочинения греческих авторов стали настольными руководствами арабских ученых.

Математика стран ислама включала в себя также знания, полученные в Индии, Вавилона, Персии, Хорезма. Позднее приобрели значение научные связи с Китаем, хотя прямых переводов с китайского на арабский, насколько известно, не было.

Большое значение для развития математики имели труды Мухаммеда ал-Хорезми (783 – около 850). Астроном: составлял зидж, т. е. астрономические и тригонометрические таблицы (таблица синусов и введен тангенс), необходимые для решения задач астрономии. Географ: написал трактат «Книга картины Земли» - первый труд по географии на арабском языке. Математик: написал трактат «Краткая книга восполнения и противопоставления». В теоретической части излагается теория линейных и квадратных уравнений. В практической части алгебраические методы применены к решению конкретных хозяйственных, торговых и юридических задач.

Абу- Камил, выходец из Египта, в конце IX – в начале X веков опубликовал трактат «Книга об ал-джабр и ал-мукабала», в котором проводит сложные преобразования над иррациональными величинами и , в частности, использует формулу , а > в > 0.

В трудах персидского математика ал-Караджи были изучены уравнения, квадратные относительно xⁿ, исследованы многие неопределенные уравнения, например, , составлена таблица для (а + в)ⁿ до n = 12.

Первые дошедшие до нас сочинение, в котором содержится общая формула для (а + в)ⁿ , n – любое натуральное число, принадлежит Насир ад-Дину ат-Туси (1265 г.). Однако в силу разобщения между мусульманским и христианским миром и даже между мусульманами Востока и Запада, многие достижения математиков стран ислама, стали известны в Европе так поздно, что к этому времени европейские математики самостоятельно пришли к этим и еще более сильным результатам. Так, Ньютон для разложения функции в бесконечные ряды широко использовал формулу, которую сейчас называют биномом Ньютона (где n – любое действительное число):

Замечательных результатов добились ученые стран ислама в изучении уравнений третьей и частично четвертой степени.

Багдадский математик Сабит ибн Корра перевел сочинение Архимеда «О шаре и цилиндре», где была приведена задача о делении шара плоскостью на два сегмента так, чтобы объемы этих сегментов находились в данном отношении. Первым кто заинтересовался этой дадачей был ал-Махани, который сумел придать ей форму уравнения х³ + r = px², но не смог уравнение решить. Через столетие это сделали Абу Джафар ал-Хазин из Хорасана и работавший в Каире Абу Али ибн ал-Хайсам.

Замечательных результатов добились ученые стран ислама в изучении уравнений третьей и частично четвертой степени.

Арабские ученые использовали методы, разработанные в Древней Греции: метод вставок, метод конических сечений и другие.

Античная наука обращалась к кубическим уравнениям лишь эпизодически. На арабском Востоке над этой проблемой работали многие математики, в результате чего был накоплен большой материал. Возникла необходимость в его систематизации, в построении общей теории.

Это сделал Омар Хайям (1048 – 1131) – выдающийся математик, астроном, философ и поэт, широко известный в наши дни как автор знаменитых четверостиший.

Он родился в городе Нишапуре (север Ирана) в области Хорасан, жил и работал в Самарканде, Бухаре и других городах Средней Азии и Ирана. В трудное время политических неурядиц, воин, страшных разрушений и массовых убийств жизнь ученого была очень тяжела. Хайям испытывал нужду, страдал из-за религиозных преследований. Лишь изредка он имел возможность спокойно заниматься наукой. Так некоторое время ему покровительствовал богатый вельможа Абу-Тахир, предположительно главный судья Самарканда, и Омар Хайям написал замечательный алгебраический трактат «О доказательствах задач алгебры и алмукабалы», посвященный решению кубических уравнений. В этом трактате Хайям писал: «Мы были свидетелями гибели ученых, от которых осталась малочисленная, но многострадальная кучка людей».

Когда Хайям был молодым, Среднюю Азию и Иран завоевали кочевник турки – сельджуки. В 1074 г. Ученый был приглашен в столицу сельджуков Исфахан (Иран) для работы в астрономической обсерватории, где ему оказали покровительство визирь Низам ал-Мулк и султан Маликшах.

Хайям стал главой обсерватории. Он работал над реформой иранского солнечного календаря, проводил астрономические наблюдения, составил «Маликшахские астрономические таблицы», написал выдающийся математический трактат «Комментарии к трудным постулатам книги Евклида».

Параллельно с занятиями наукой Хайям создавал свои четверостишия («Рубаи»). Научные труды Хайям писал на арабском языке, стихотворения на персидско-таджикском наречии.

В 1092 году был убит Низам ал-Мулк и умер Маликшах. Реформа календаря не осуществилась. Была закрыта обсерватория. Хайям, который в своих стихах высмеивал догмы официальной религии, был обвинен в безбожии. На старости лет он вынужден был совершить паломничество в Мекку. Хайям скончался в бедности в родном Нишапуре.

В трудах персидского математика ал-Караджи были изучены уравнения, квадратные относительно xⁿ, исследованы многие неопределенные уравнения, например, , составлена таблица для (а + в)ⁿ до n = 12.

В трактате «Трудности арифметики» Омар Хайям, по-видимому, нашел общую формулу для возведения бинома (а + в) в степень n. Однако этот трактат утерян. Первые дошедшие до нас сочинение, в котором содержится общая формула для (а + в)ⁿ , n – любое натуральное число, принадлежит Насир ад-Дину ат-Туси (1265 г.).

Хайям развил геометрическую теорию кубических уравнений. В своем алгебраическом трактате он высказал мысль о том, что уравнения третьей степени нельзя решить с помощью циркуля и линейки. Хайям подчеркнул, что их решение «может быть, произведено только при помощи конических сечений».

Хайям рассматривал уравнения с произвольными положительными коэффициентами и разыскивал положительные корни. Он дал классификацию кубических уравнений, выделив 19 классов, из которых 5 классов сводится к линейным или квадратным (dx³ = cx², dx³ = bx и другие) Для каждого из остальных 14 классов (dx³ = a; dx³ +bx = a и так далее) Хайям указал метод решения с помощью конических сечений: парабол, равносторонних гипербол и окружностей.

Как и все математики Востока, Хайям описывал уравнения словесно. Так фраза «Куб и корни равны числу» у него означает уравнение х³ + bx = a. Чтобы его решить, Хайям рассмотрел окружность и параболу .

Рис 20.

Абсцисса точки пересечения кривых, которая не совпадает с началом координат, есть корень данного уравнения. Действительно, можно записать систему: 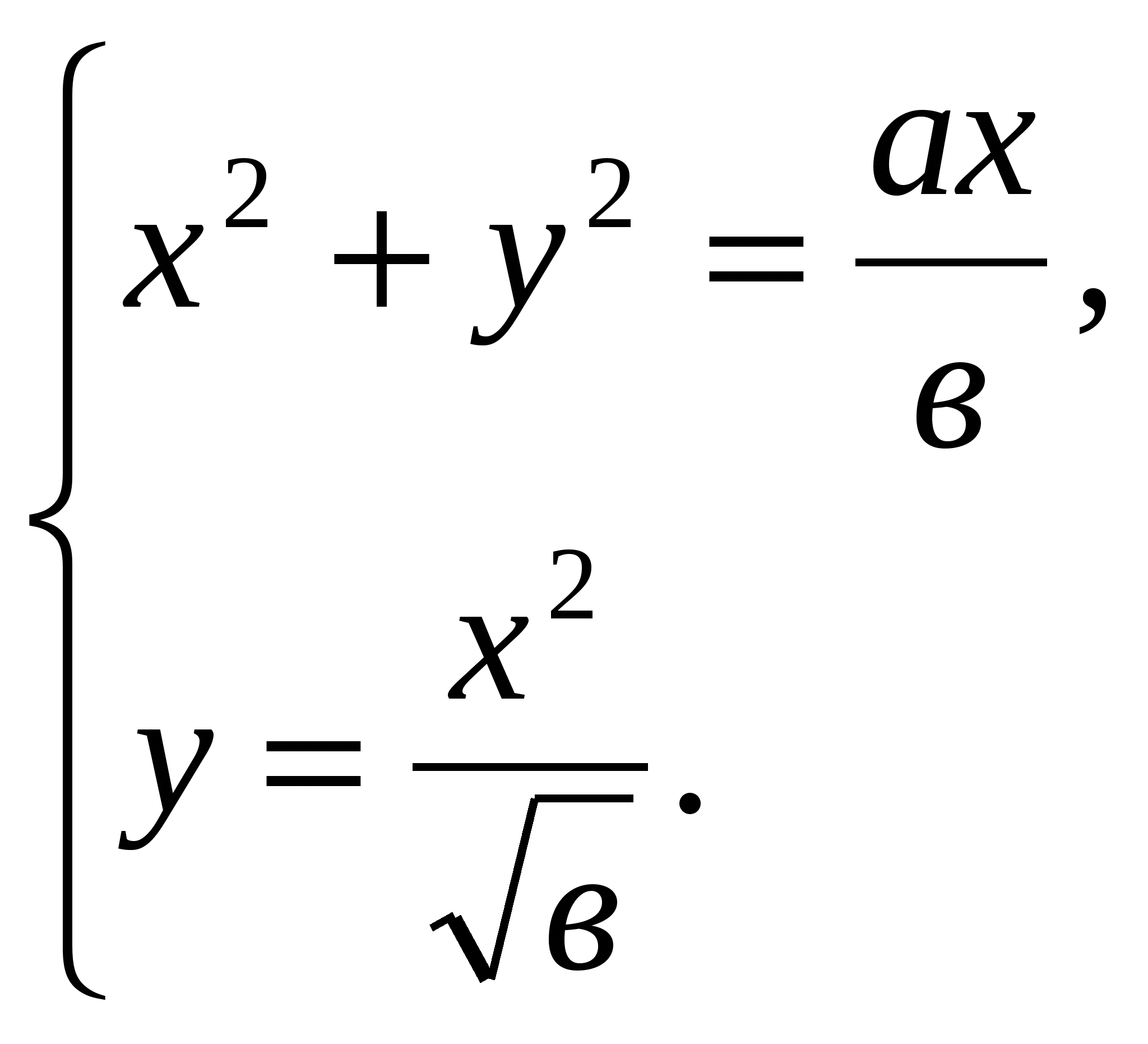Отсюда при получаем , .

Для каждого из 14 классов Хайям решал вопрос о числе положительных корней в зависимости от условий, накладываемых на коэффициенты уравнений. Так он указал, что уравнение х³ + bx = a всегда имеет единственный положительный корень. Лишь рассматривая класс уравнений х³ + вх = сх² + а, Хайям допустил неточность, не заметив, что оно может иметь три положительных корня. Эту возможность открыл в XVI веке Дж. Кардано.

Хайям поставил проблему решения кубических уравнений в радикалах с помощью алгебраической формулы, но не сумел решить ее и написал: «Может быть, кто-нибудь из тех, кто придет после нас, узнает это».

Формулы для решения кубических уравнений нашли в XVI веке итальянские математики Ш. дель Ферро и Н. Тарталья, а опубликовал Кардано в 1545 г.

Омар Хайям навсегда вошел в историю всемирной культуры не только как блестящий ученый энциклопедист, но и как прекрасный поэт, который воспевал свободу, бичевал ханжество и лицемерие, высмеивал суеверия. Его мудрые лирические четверостишия, наполненные глубоким философским смыслом, в XIX и XX веках были переведены на все основные языки мира.