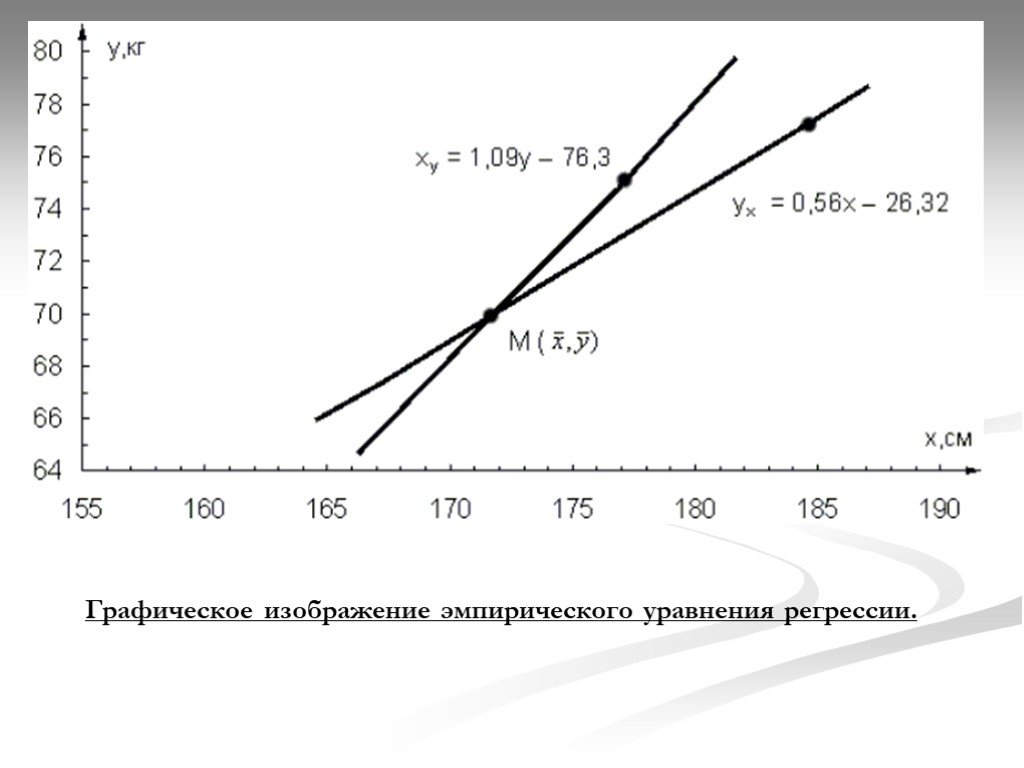
Презентация "Регрессионный анализ" – проект, доклад
Презентацию на тему "Регрессионный анализ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Экономический анализ сказки П. П. Ершова «Конёк-горбунок»
«Братья сеяли пшеницу Да возили в град-столицу: Недалече от села. Там пшеницу продавали, Деньги счетом принимали И с набитою сумой Возвращалися домой». ...Факторный анализ
Факторный анализ — многомерный метод, применяемый для изучения взаимосвязей между значениями переменных. Предполагается, что известные переменные ...Формы половозрастных пирамид и анализ половозрастной пирамиды Республики Беларусь
Половозрастные пирамиды — графическое представление распределения населения по полу и возрасту, использующееся для характеристики половозрастного ...Учет денежных средств организации и анализ их движения
Объект исследования – общество с ограниченной ответственностью «Нателла». Предмет исследования – финансовые процессы на предприятии, связанные с формированием ...Учет и анализ финансового состояния предприятия
Тема данной дипломной работы актуальна тем, что показывает необходимость анализа финансового состояния для повышения доходности капитала, обеспечения ...Тема 9. Структура инвестиционного проекта : его анализ и жизненный цикл
1. Понятие и содержание инвестиционного проекта. Реализация целей инвестирования предполагает формирование инвестиционных проектов. Понятие инвестиционного ...Тема лекции 11. Функционально-стоимостной анализ (ФСА): цели, задачи, методы и порядок проведения
Одной из важнейших задач любого предприятия в условиях рыночной экономики является обеспечение конкурентоспособности продукции на рынке. Для решения ...Рынки труда: микроэкономический анализ
Рынок труда представляет собой совокупный спрос и предложение рабочей силы, который за счет взаимодействия этих двух составляющих обеспечивает размещение ...Статистический анализ данных с использованием microsoft excel
Статистический анализ данных в Excel 2007 осуществляется через панель быстрого доступа (синее поле на уровне вкладок). Панель быстрого доступа /Настройка ...Комплексный анализ креолизованного рекламного текста
. Интегративный креализованный текст (вербальную и визуальную части нельзя понять друг без друга). Визуальный знак – гетерогенный и несет в себе. ...Оценка человеческого капитала: анализ подходов и методик.
Из теории менеджмента известно, что управлять можно только тем объектом, который подвергается измерению. (Чеботарев Н.Ф.). Оценка человеческого капитала. ...Клинический анализ кала
Определение pH Определение скрытой (не видимой глазом) крови Определение билирубина Определение стеркобилина Определение белка Определение лейкоцитов*. ...Интеллектуальный анализ данных
Выбранная область и задачи ИАД. Область: телекоммуникации, анализ записей Задачи: Классификация Обнаружение аномалий Частотный анализ. Классификация. ...ВВЕДЕНИЕ В прикладноЙ анализ поведения
Тем навыкам, которых не хватает по сравнению с другими детьми этого же возраста. Или ответив на вопросы: Что в данное время вы делаете за ребенка, ...Анатомический анализ положения тела: «мост»
План АНАЛИЗА:. Описание морфологии положения или движения тела. Характеристика положения или движения тела с позиций законов механики. Характеристика ...Анатомический анализ движений тела: Сальто назад с места
Сальто назад с места-это…. Это сложное ациклическое вращательное движение, которое заключается в отталкивании тела от опорной поверхности, полете ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 февраля 2019
Категория:Разные
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию