Презентация "Площади многоугольников" по математике – проект, доклад
Презентацию на тему "Площади многоугольников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Площади многоугольников
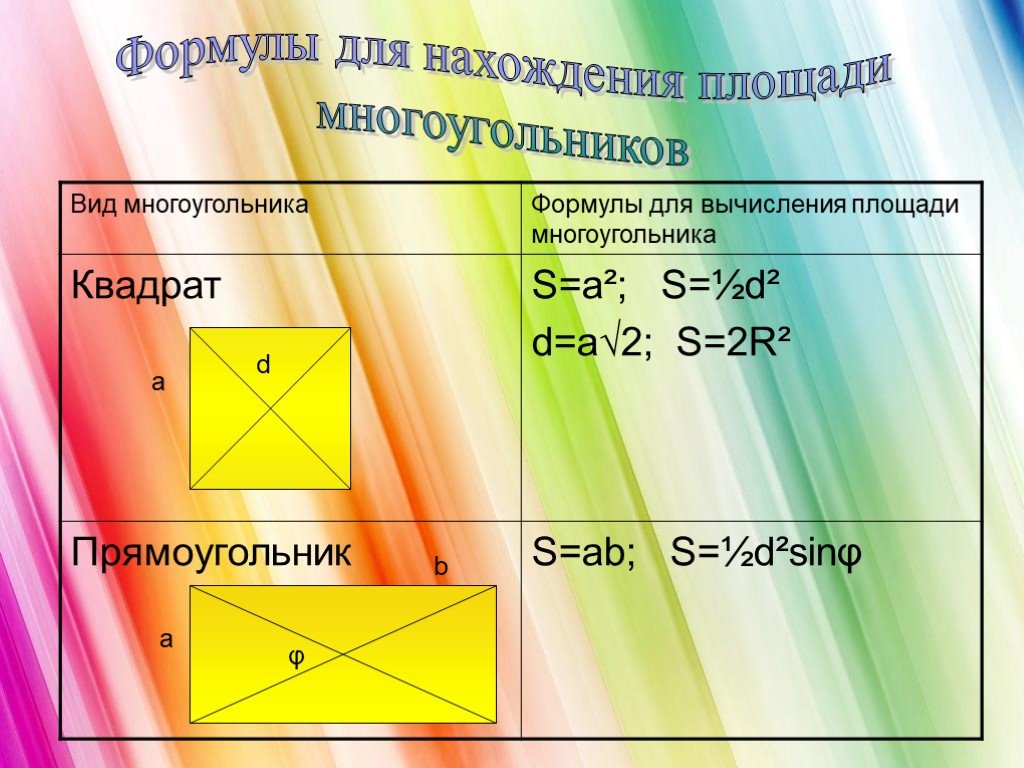
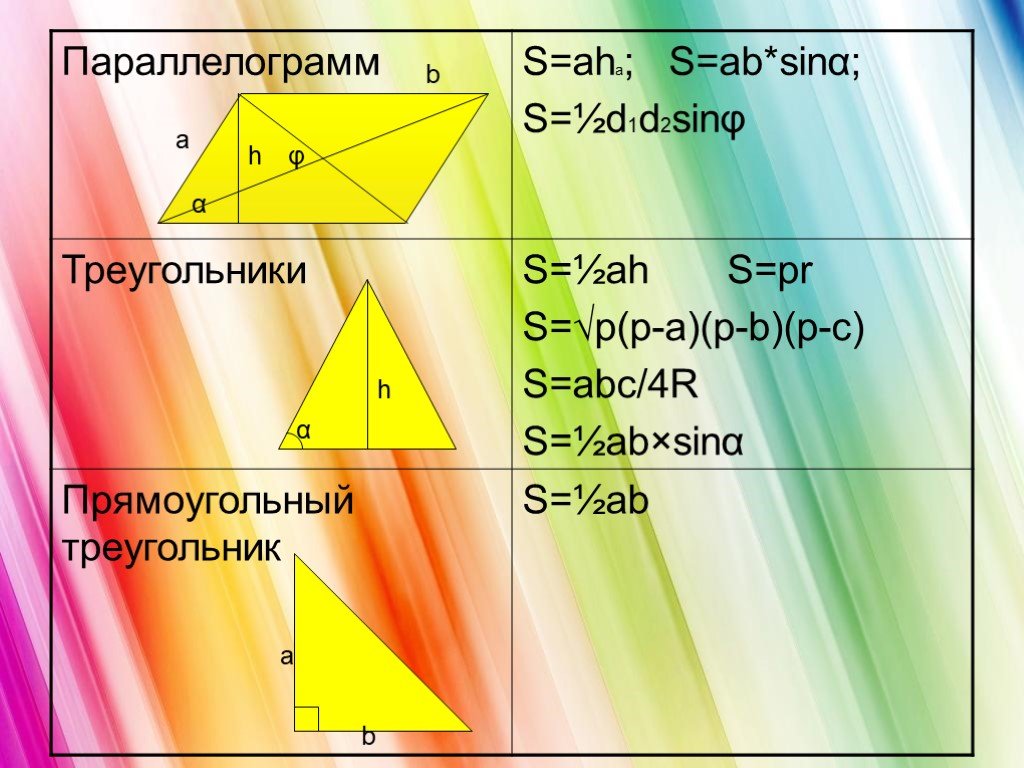
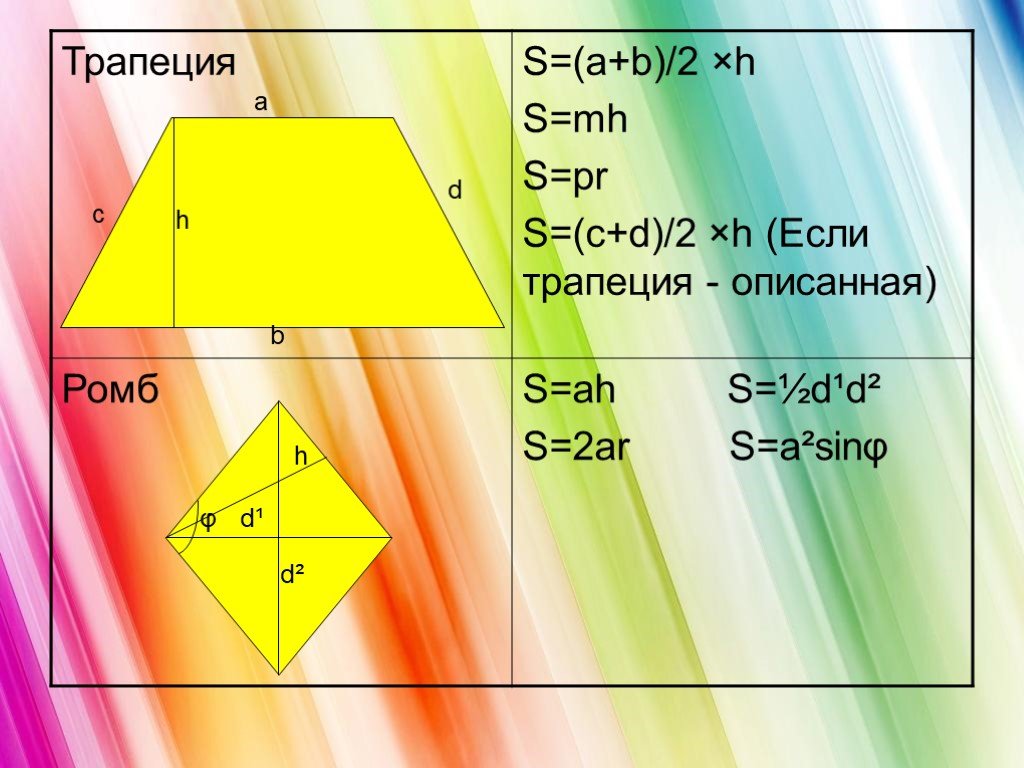
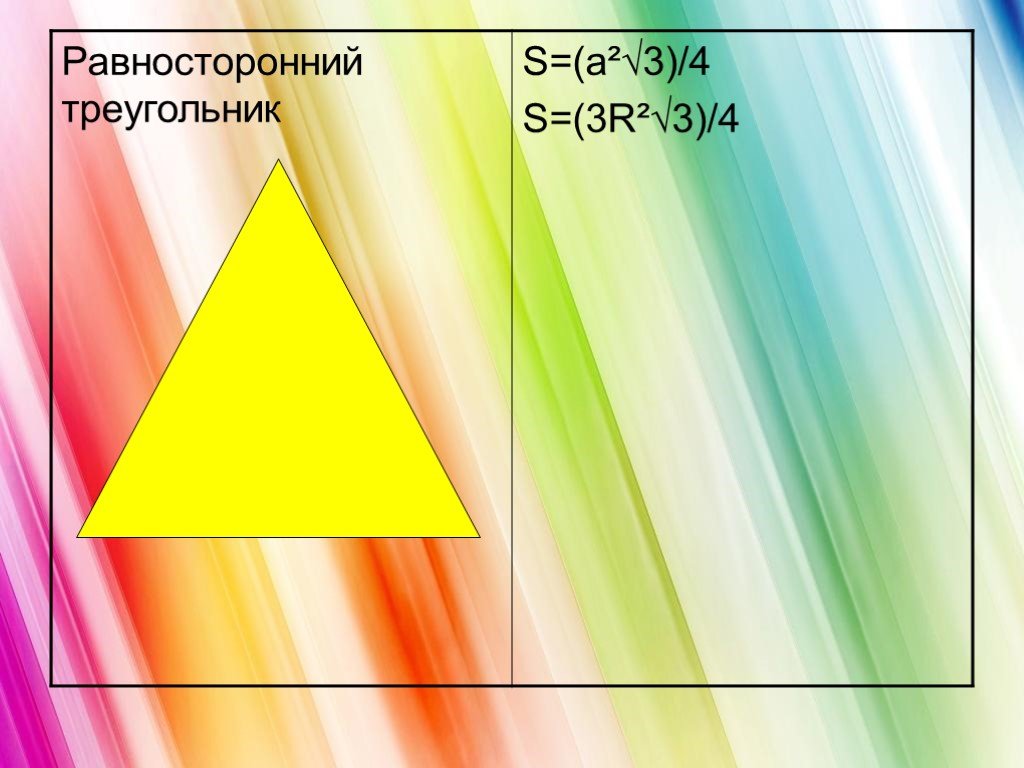
Площади многоугольников. Площадь многоугольника. Основные свойства площадей. Площадь прямоугольника. Площадь параллелограмма. Площадь треугольника. ...Площади многоугольников
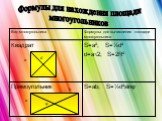
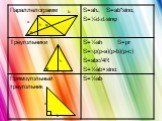
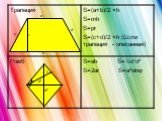
Содержание:. 1. Виды многоугольников. 2. Свойства измерения площадей. 3. Основные формулы для вычисления площадей геометрических фигур: Треугольник ...Преобразование Наполеоном многоугольников
Содержание: 1. Введение. 2. Преобразование Наполеона треугольников. а) Преобразование Наполеона вложенных фигур. б) Ядро линейного преобразования. ...Тест по теме "Площади"
ЗАДАНИЕ № 1. Чему равна площадь фигуры? ЗАДАНИЕ № 2. ЗАДАНИЕ № 3. ЗАДАНИЕ № 4. ЗАДАНИЕ № 5. ЗАДАНИЕ № 6. ЗАДАНИЕ № 7. ЗАДАНИЕ № 8. ЗАДАНИЕ № 9. ЗАДАНИЕ ...Подобие правильных многоугольников
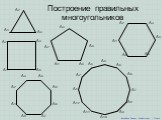
Цели:. доказать теорему о подобии правильных выпуклых n-угольников, свойство о том, что отношение периметров правильных n-угольников равно отношению ...Построение правильных многоугольников
В заданиях на построение используются: карандаш, линейка(для проведения прямых, лучей и отрезков) и циркуль(для построения окружностей и дуг). I. ...Нахождение площадей многоугольников
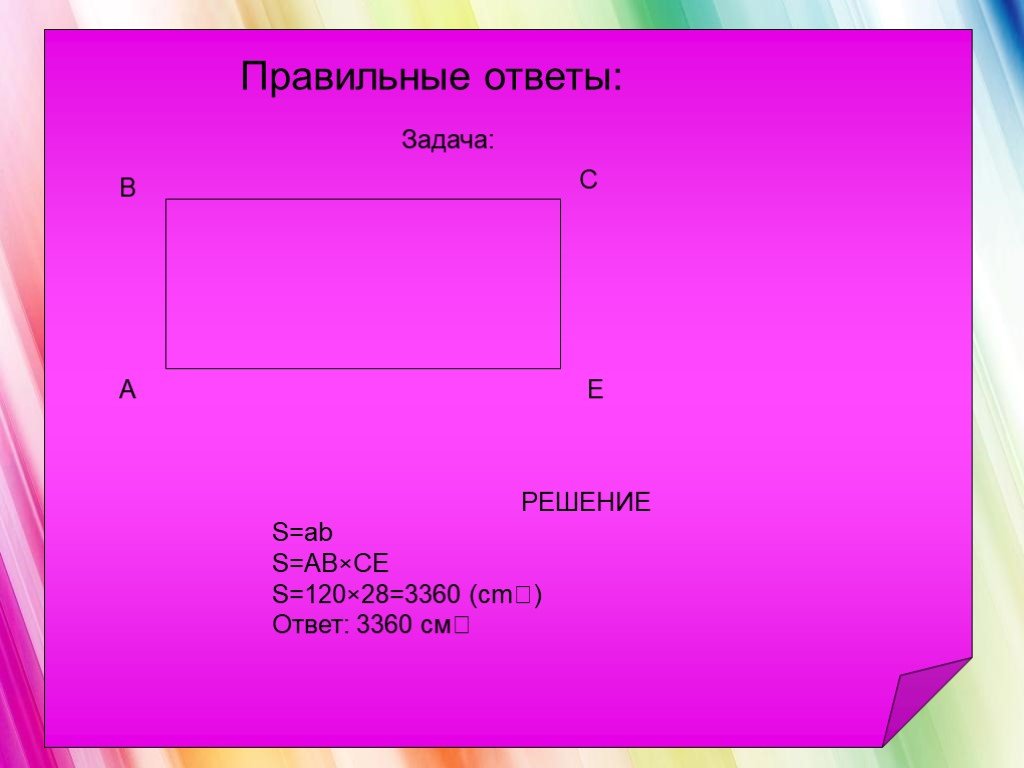
Математика, друзья, Абсолютно всем нужна. На уроке работай старательно, И успех тебя ждет обязательно! S=ab S=a·a. Тема урока: «Нахождение площадей ...Площадь многоугольников
Площадь правильного многоугольника, формула. Для того чтобы вычислить площадь правильного многоугольника его разбивают на равные треугольники с общей ...Площади комбинированных фигур
Разминка №1. Я задумал число. Если к половине этого числа прибавить четверть его, то получится 18. какое число я задумал? Решение ? 18. №2. В доме ...Площади фигур. Зачёт
закрепить навык в решении задач на нахождение площадей фигур; развивать мышление, внимание. Цель:. Купи трапецию Купи параллелограмм. Купи фигуру. ...Площади и объёмы
Вспомним формулу S = v·t. 1. Найдите по формуле путь, если скорость равна 106 км/ч, а время 13 часов. 2. Вычислите время движения автомобиля, если ...Площади и объёмы
Домашняя работа. № 828Решение: 1) 8 10 6 = 480 (см3) – объем параллелепипеда. 2) (8 6)2 + (8 10)2+(610)2 = 96 +160 +120 = 376(см2)- площадь ...Площади и объемы
Работа с формулами. Ркв = ? Sкв = ? Sпр = ? Рпр = ? Vпар = ? Vк = ? Назовите единицы измерения площадей. 1 см. Назовите единицы измерения объемов. ...Площади
Разминка для ума. 15А-математический тренажёр. начало конец 31 ·4 +900 +37 :х -х + -10 ·14 :7. Из какой сказки слова: «…а дорога далека, а корзина ...Площади
Личные данные. Образование: высшее механико-математический факультет ГГУ имени Лобачевского специальность математика присвоена квалификация математик-преподаватель ...Интеллектуальная игра на тему "Площади плоских фигур"
Обобщить и систематизировать знания учащихся по теме «Площади плоских фигур»: Повторить определения и свойства фигур, формулы для вычисления площади. ...Площади четырехугольников
Параллелограмм А В С D. Параллелограмм есть четырехугольник, противоположные стороны которого попарно параллельны. Любые две противоположные стороны ...Площади фигур геометрия
Площадь- это.. Квадратный сантиметр- это площадь квадрата со стороной 1 см.. Что бы найти площадь фигуры надо определить, сколько таких квадратов ...Площадь многоугольников
Чему равна площадь квадрата? Чему равна площадь прямоугольника? а b. запишите формулу площади треугольника. найдите площадь трапеции и запишите эту ...Площади фигур. Теорема Пифагора
Установите соответствие между фигурой и формулой площади. . Задача № 1. В треугольнике два угла равны 45 и 90 , а большая сторона 12 см. Найдите 2 ...Конспекты
Площади многоугольников. Решение задач
8 класс. Тема:. Площади многоугольников. Решение задач. Цель урока. :. . Обобщить знания о площадях многоугольников. . Рассмотреть различные ...Площади многоугольников
Автор: Вовденко Ольга Леонидовна, учитель математики. Место работы: МБОУ СОШ № 61 имени М.И. Неделина г. Липецк. . Конспект урока на тему «Площади ...Площади многоугольников
Методическая разработка урока геометрии по теме "Площади многоугольников" для 8 класса с использованием информационно коммуникационных технологий. ...Площади четырехугольников
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №3». Островского района Псковской области. Конспект ...Площади четырёхугольников
Тема урока:. Площади четырёхугольников. Предмет:. геометрия. Класс. : 8. . Тип урока. : повторительно-обобщающий. Оборудование урока. : ...Площади фигур
Урок математики в 3Б классе по теме «Площади фигур» ( программа «Перспектива»). Планируемые результаты:. Личностные: развитие навыков сотрудничества ...Площади фигур
Урок по теме: « Площади фигур» - 8 класс. 19.12.2014. Учитель математики Дорофеева М.Я. МКУ « Атагайская СОШ». Нижнеудинского района. Иркутской ...Площади фигур
Конспект урока для 8 класса по геометрии "Площади фигур". Цели урока:. повторить пройденный материал, вывести формулу нахождения площади прямоугольного ...Площади и объемы
МБОУ «Овгортская общеобразовательная школа-интернат». Конспект урока по математике«Площади и объемы ». (5 класс). . подготовила. ...Построение правильных и полуправильных многоугольников
МКОУ В(С)ОШ № 2 ст. Александрийской. Георгиевского района. Ставропольского края. Урок в 10 классе по теме:. "Построение правильных и полуправильных ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 февраля 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию