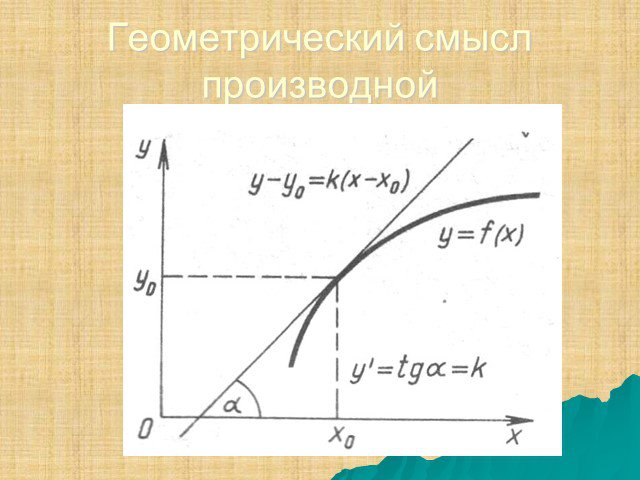
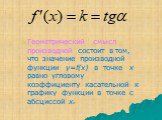Презентация "ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ" по математике – проект, доклад
Презентацию на тему "ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ
Учитель математики Маеренкова Вера Васильевна. ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ. Цели урока: Образовательные: экспериментальным ...ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
Построение графика функции y = sin x. . . Функция у = sin x. 3. Функция у = sin α нечетная, т.к. sin (- α) = - sin α. 1. Областью определения функции ...ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
Повторим? Назовите координаты вершин парабол, ось симметрии. Сформулируйте правила построения графиков функций у=ах2 + n, у=а(х-m)2, у=а(х-m)2 + n. ...Обобщающий урок по теме ФУНКЦИИ
Ответьте на вопросы! Что называется функцией? Что называется аргументом? Что называется областью определения функции? Что называется графиком функции? ...НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
(x²)′= (2x³)′= (7x)′= (10)′= (128 )′= (5x² + 3x - 9 )′= x² 6x² 0 7 10x + 3. АЛГОРИТМ. Найти точки экстремума функции, т. е. точки в которых производная ...ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ
Цели. Определить взаимное расположение графиков линейных функций. Выяснить геометрический смысл коэффициентов b u k. Постройте в одной системе координат ...АНАЛИЗ ИНТЕГРАЛЬНОЙ ФУНКЦИИ
Анализаторные функции новой коры. Анализаторные функции новой коры. Зрение. Проводящие пути зрительного анализатора. Первичная зрительная кора (поле ...Конспекты
ПОНЯТИЕ ЛИНЕЙНОЙ ФУНКЦИИ И ЕЁ ГРАФИК
тЕМА:Понятие линейной функции и её график. Цели:. ввести понятие линейной функции; формировать умение выделять линейную функцию из множества функций; ...ПОНЯТИЕ ФУНКЦИИ у = sin х. ГРАФИК ФУНКЦИИ у = sin х
Урок. 1. Понятие функции. у. =. sin. х. . График функции. у. =. sin. х. Цели:. ввести понятие функции. у. =. sin. х. и выделить её основные ...НАХОЖДЕНИЕ СВОЙСТВ ФУНКЦИИ ПО ЕЕ ГРАФИКУ
Алгебра 9 класс. Тема урока: Нахождение свойств функции по ее графику. Цели:. познакомить учащихся с основными свойствами функций; формировать ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:27 декабря 2012
Категория:Математика
Автор презентации:Пак Н.Н., учитель математики
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию