Конспект урока «ПОНЯТИЕ ЛИНЕЙНОЙ ФУНКЦИИ И ЕЁ ГРАФИК» по алгебре
тЕМА:Понятие линейной функции и её график
Цели: ввести понятие линейной функции; формировать умение выделять линейную функцию из множества функций; определить график линейной функции и выявить роль параметров k и b в расположении графика линейной функции.
Ход урока
I. Устная работа.
1. Какие из функций являются прямой пропорциональностью:
а) у = 13х; б) у = ![]() ; в) у =
; в) у = ![]() ;
;
г) у = 13(х – 2); д) у = 13х2; е) у =  ?
?
2. Какая из точек принадлежит графику функции, заданной формулой у = ![]() :
:
а) (0; –2); б)  ; в) (4; –2);
; в) (4; –2);
г) (0; 0); д)  ; е)
; е)  ?
?
3. График линейной пропорциональности проходит через точку А. Найдите коэффициент пропорциональности, если:
а) А  ; б) А (2; –6); в) А
; б) А (2; –6); в) А  ;
;
г) А  ; д) А (0; 0); е) А (3; –0,3).
; д) А (0; 0); е) А (3; –0,3).
II. Объяснение нового материала.
Весь материал целесообразно разбить на несколько логических частей и на каждом уроке изучать одну из них.
На этом уроке целесообразно рассмотреть два вопроса: понятие линейной функции и влияние параметров k и b на расположение графика линейной функции.
В соответствии с этим объяснение проводится в два этапа.
1. Введение понятия линейной функции.
Понятие линейной функции начинаем изучать с рассмотрения реальных процессов и реальных ситуаций.
Необходимо привести примеры из учебника и вынести полученные формулы на доску:
s = 50t + 20, где t ≥ 0;
y = 3x + 5, где x N.
Далее можно спросить учащихся: что общего во всех этих формулах? Затем сообщить им, что зависимости такого вида называются линейными функциями, и дать четкое определение.
На доску может быть вынесена запись:
2. Определение прямой пропорциональности как частного случая линейной функции.
Обращаем внимание учащихся, что в отличие от определения прямой пропорциональности, где k 0, в формуле линейной функции коэффициенты k и b – любые числа, то есть могут равняться нулю. Причем как по отдельности, так и одновременно.
В случае если k 0 и b = 0, функция у = kx + b принимает вид у = kx, то есть является прямой пропорциональностью. Сразу делаем вывод: графиком линейной функции в этом случае является прямая, проходящая через начало координат, и для её построения необходимо вычислить по формуле координаты ещё одной точки.
3. График линейной функции и роль параметров k и b в её расположении.
а) Следующим шагом целесообразно рассмотреть случай k 0 и b 0. Заполняем таблицу со с. 71 учебника для функций у = 0,5х и у = 0,5х + 2. Анализируя полученные данные, учащиеся делают вывод: графиком функции у = 0,5х + 2 является прямая, параллельная прямой, являющейся графиком функции у = 0,5х, и любая точка графика получается сдвигом по оси у на 2 единицы вверх.
Устное упражнение.
Что является графиком функции у = 3х + 1; у = –1,5х + 2; у = 2х – 14; у = –3х – 1,5?
б) Рассматриваем случай k = 0, b 0. Функция у = kx + b принимает вид у = b. Получаем, что, независимо от значения х, у всегда равно b. Значит, графиком функции является прямая, параллельная оси х и проходящая через точку (0; b).
в) Рассматриваем случай k = 0, b = 0. Функция у = kx + b принимает вид у = 0, то есть графиком является сама ось х.
После этого на доску можно вынести запись:
4. Последним шагом формулируем простейший алгоритм построения графика линейной функции:
1-й шаг. По формуле найти координаты двух точек графика.
2-й шаг. Отметить полученные точки на координатной плоскости.
3-й шаг. Провести через построенные точки прямую.
III. Формирование умений и навыков.
1. Рассматриваем примеры 3–5 со с. 72–73 учебника. Во время работы учащиеся должны называть значения коэффициентов k и b.
2. Определите, какие из следующих функций являются линейными. Назовите для них значения коэффициентов k и b.
а) у = 2,5x – 7; б) у = 4 – ![]() x; в) у = 4x – 5x2;
x; в) у = 4x – 5x2;
г) у = ![]() ; д) у = –3х; е) у =
; д) у = –3х; е) у = ![]() ;
;
ж) у = 3x2 + 2; з) у = –5; и) у = 0.
3. Что является графиком линейной функции и как он расположен?
а) у = –3x + 5; б) у = ![]() x; в) у = –3;
x; в) у = –3;
г) у = ![]() ; д) у =
; д) у = ![]() ; е) у = 0.
; е) у = 0.
4. На рисунках изображены графики функций. Какие из этих функций являются линейными?
а) 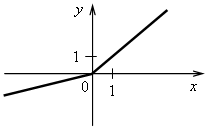 в)
в) 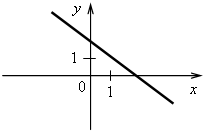
б) 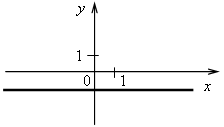 г)
г) 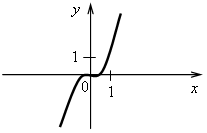
5. № 313, 315.
6. № 319, 321.
IV. Итоги урока.
– Дайте определение линейной функции.
– Что является графиком линейной функции?
– Как влияют параметры k и b на расположение графика линейной функции?
– Каков алгоритм построения графика линейной функции?
Домашнее задание: № 314; № 316 (устно); № 318; № 320.
Здесь представлен конспект к уроку на тему «ПОНЯТИЕ ЛИНЕЙНОЙ ФУНКЦИИ И ЕЁ ГРАФИК», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

