Презентация "ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ" по математике – проект, доклад
Презентацию на тему "ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
«Скалярное произведение векторов» геометрия
Таблица значений для углов, равных 300, 450, 600. Заполните таблицу. Формулы приведения. sin( )= cos( )= -. Проверка д.з. № 1039 Диагонали квадрата ...«Ломаная» геометрия
Найдите соответствие. Ответы. Ломаная Тема урока:. Какие из фигур являются ломаными? А Б В Г Д. Ответ А В Г. Кусок проволоки возьми И его ты перегни. ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...«Конус» геометрия
История изучения геометрического тела конус. С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. ...Конспекты
АРИФМЕТИЧЕСКИЙ КВАДРАТНЫЙ КОРЕНЬ ИЗ СТЕПЕНИ И ЕГО СВОЙСТВА
1001 идея интересного занятия с детьми. . РАЗРАБОТКА УРОКА ПО ТЕМЕ «АРИФМЕТИЧЕСКИЙ КВАДРАТНЫЙ КОРЕНЬ ИЗ СТЕПЕНИ И ЕГО СВОЙСТВА». Евграшина Наталья ...АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Муниципальное бюджетное общеобразовательное учреждение. Наро-Фоминская средняя общеобразовательная школа №5. с углубленным изучением отдельных ...АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ЧИСЛАМИ. УРОК ПОВТОРЕНИЯ И ЗАКРЕПЛЕНИЯ
МОУ –лицей № 90. начальная школа. «АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ЧИСЛАМИ. . . УРОК ПОВТОРЕНИЯ И ЗАКРЕПЛЕНИЯ». (конспект урока ...АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
УРОК В 9 КЛАССЕ ПО ТЕМЕ. «АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ» (2ч). Цели урока:. . 1). образовательная. : рассмотрение задач на применение ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:18 августа 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию




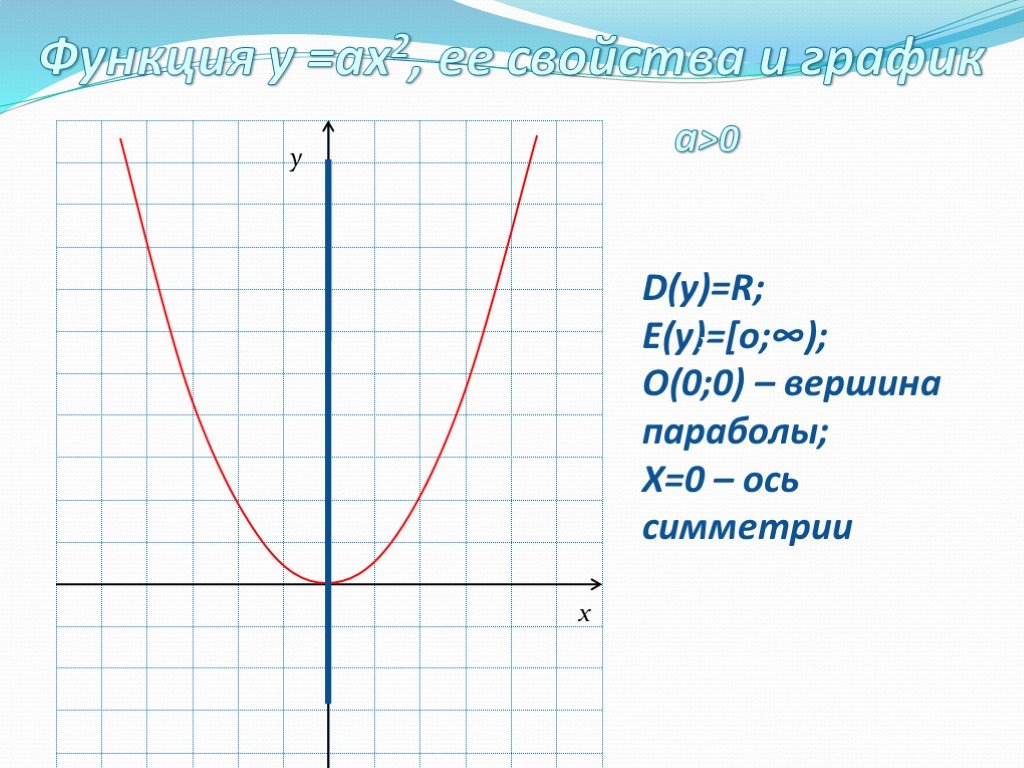
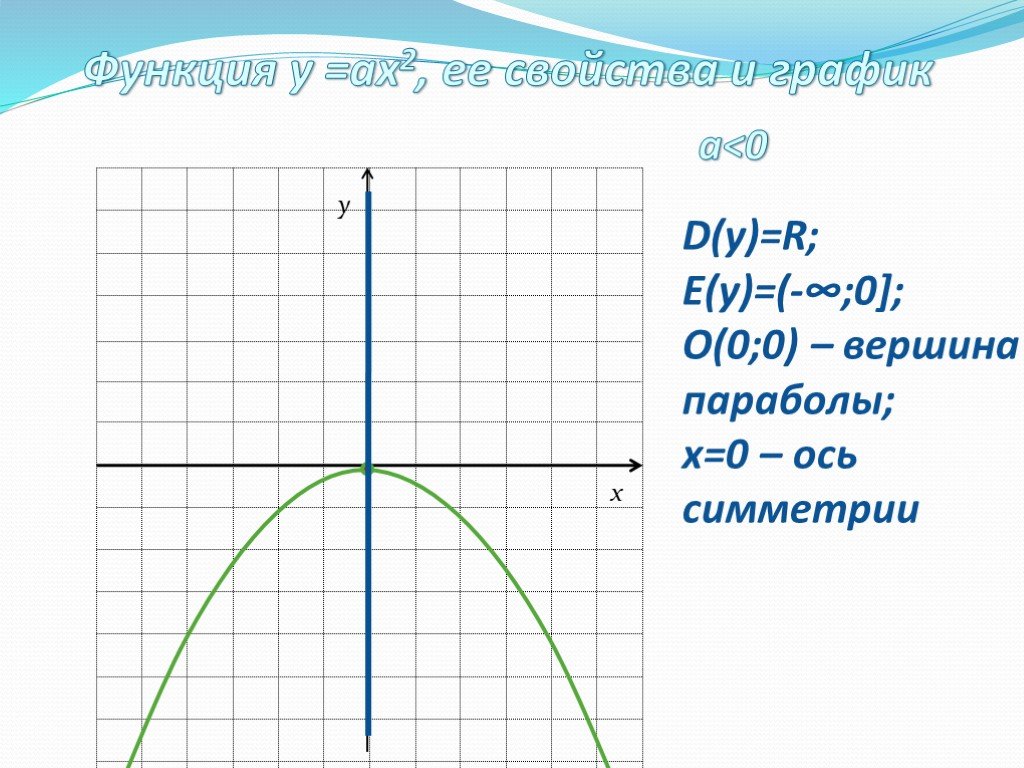

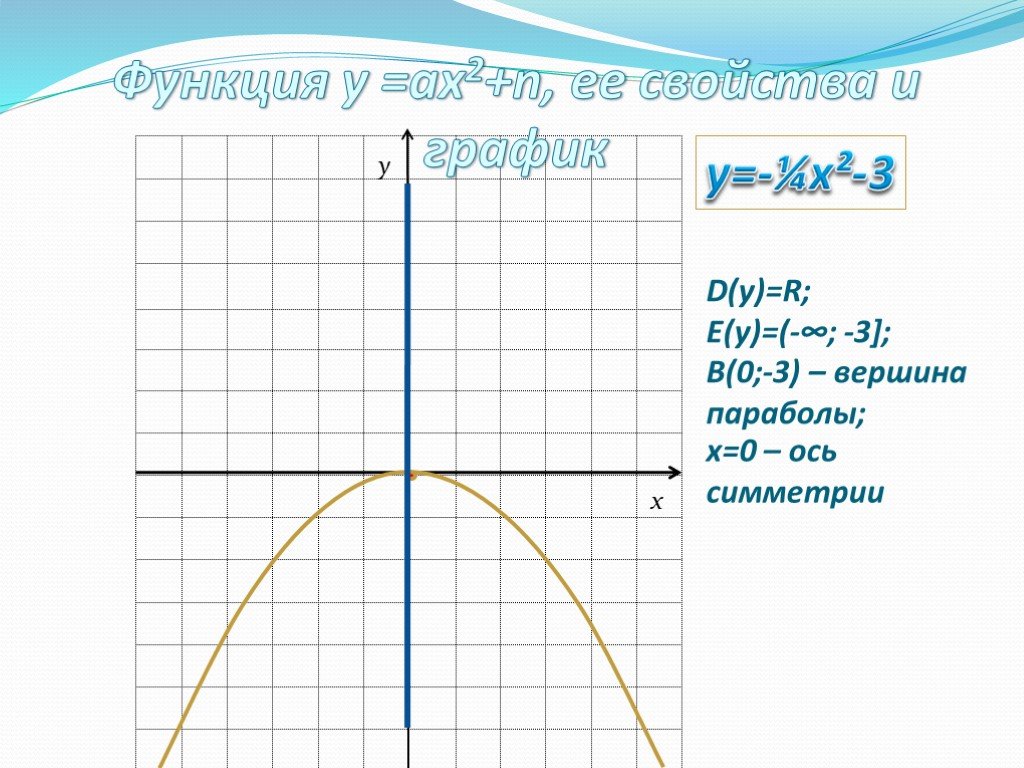

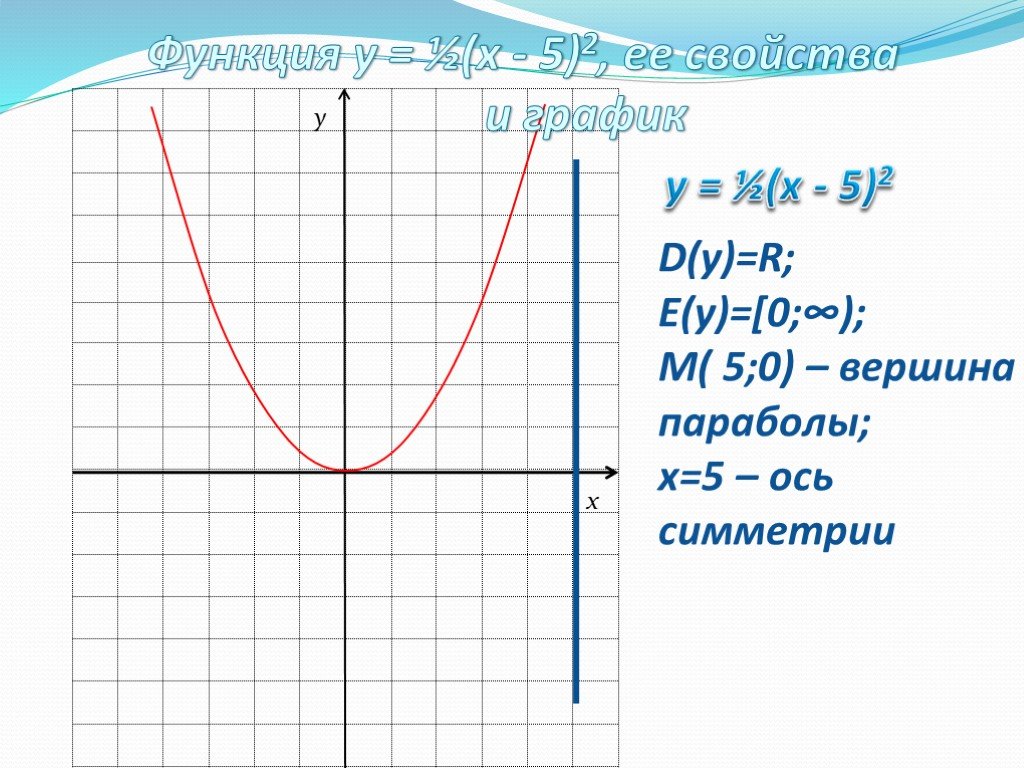











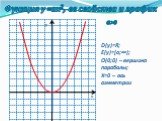

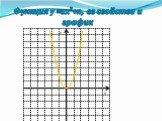
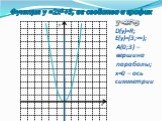
![D(у)=R; E(у)=(-∞; -3]; В(0;-3) – вершина параболы; y=-¼x²-3 D(у)=R; E(у)=(-∞; -3]; В(0;-3) – вершина параболы; y=-¼x²-3](https://prezentacii.org/upload/cloud/19/08/158204/images/thumbs/screen9.jpg)

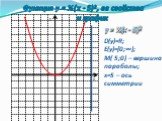
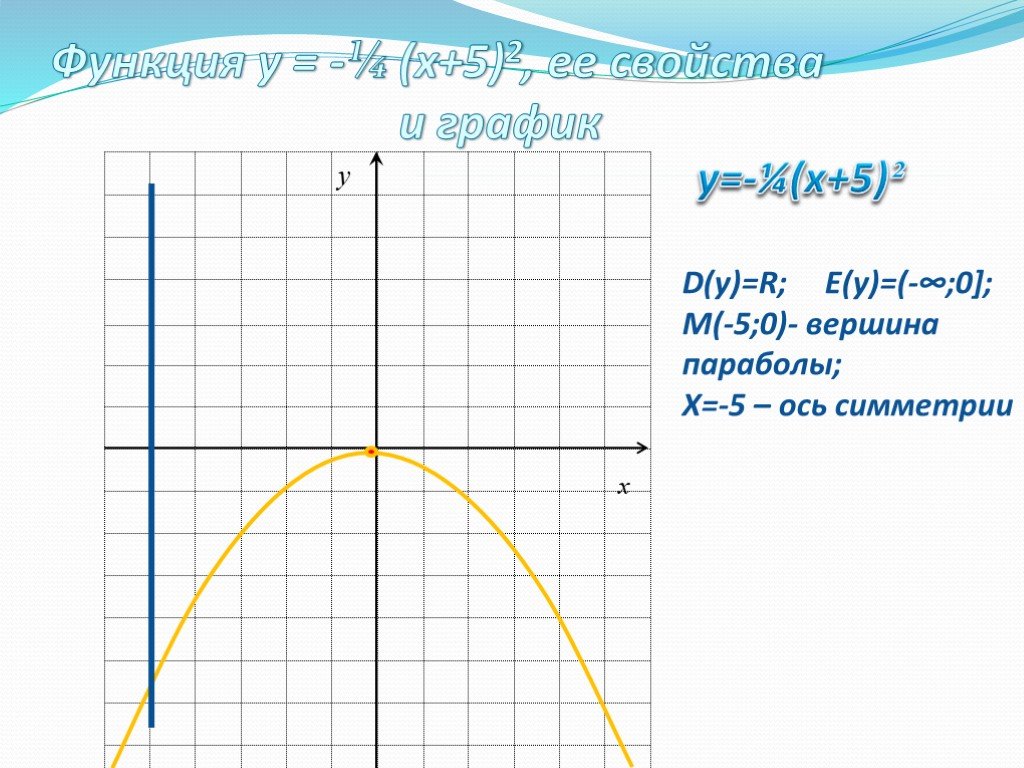
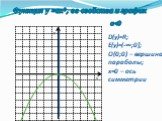
![y=-¼(x+5)². Функция у = -¼ (х+5)2, ее свойства и график. D(у)=R; E(у)=(-∞;0]; М(-5;0)- вершина параболы; Х=-5 – ось симметрии y=-¼(x+5)². Функция у = -¼ (х+5)2, ее свойства и график. D(у)=R; E(у)=(-∞;0]; М(-5;0)- вершина параболы; Х=-5 – ось симметрии](https://prezentacii.org/upload/cloud/19/08/158204/images/thumbs/screen12.jpg)

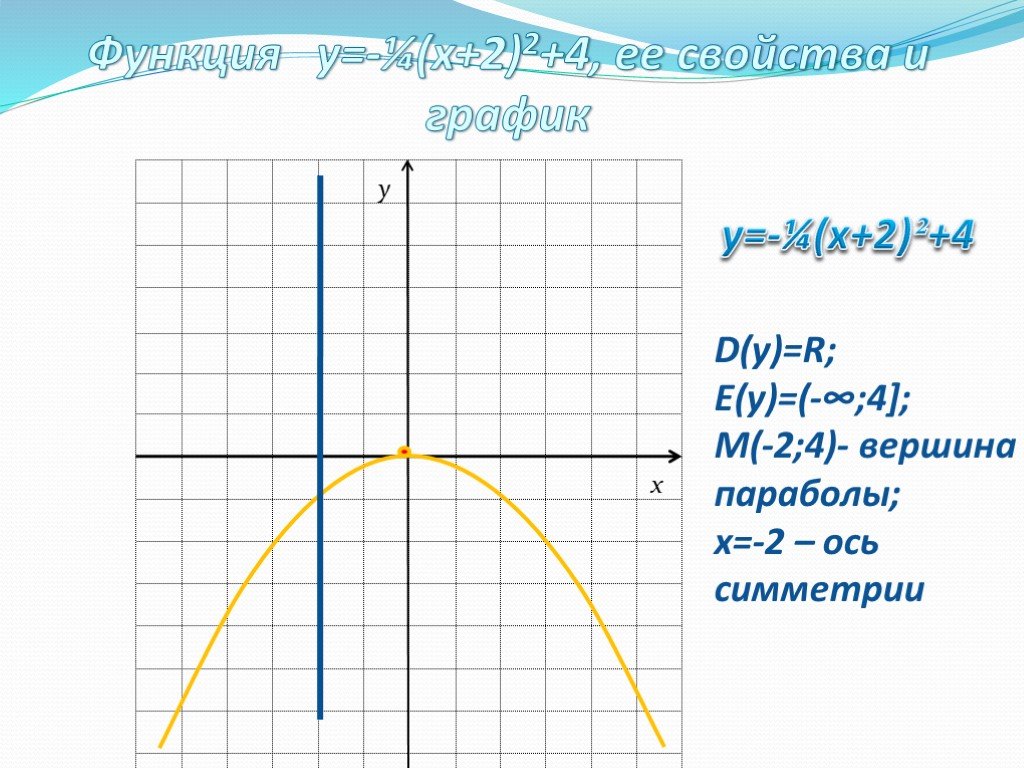
![y=-¼(x+2)²+4. Функция у=-¼(х+2)2+4, ее свойства и график. D(у)=R; E(у)=(-∞;4]; М(-2;4)- вершина параболы; х=-2 – ось симметрии y=-¼(x+2)²+4. Функция у=-¼(х+2)2+4, ее свойства и график. D(у)=R; E(у)=(-∞;4]; М(-2;4)- вершина параболы; х=-2 – ось симметрии](https://prezentacii.org/upload/cloud/19/08/158204/images/thumbs/screen14.jpg)




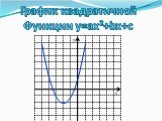

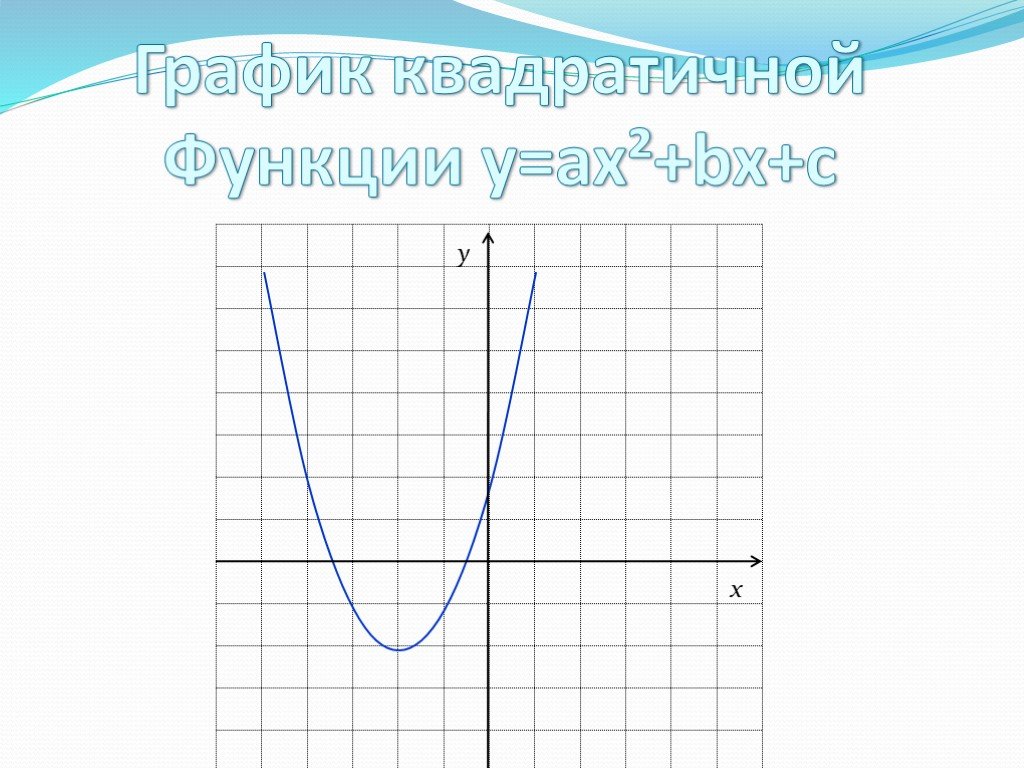
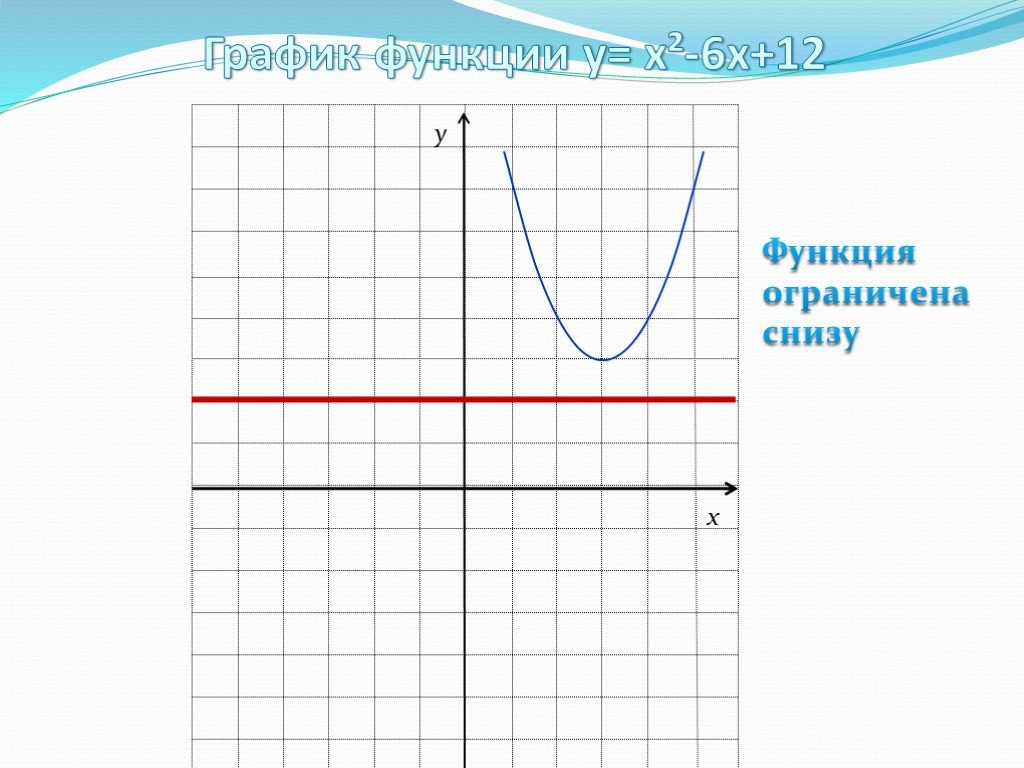
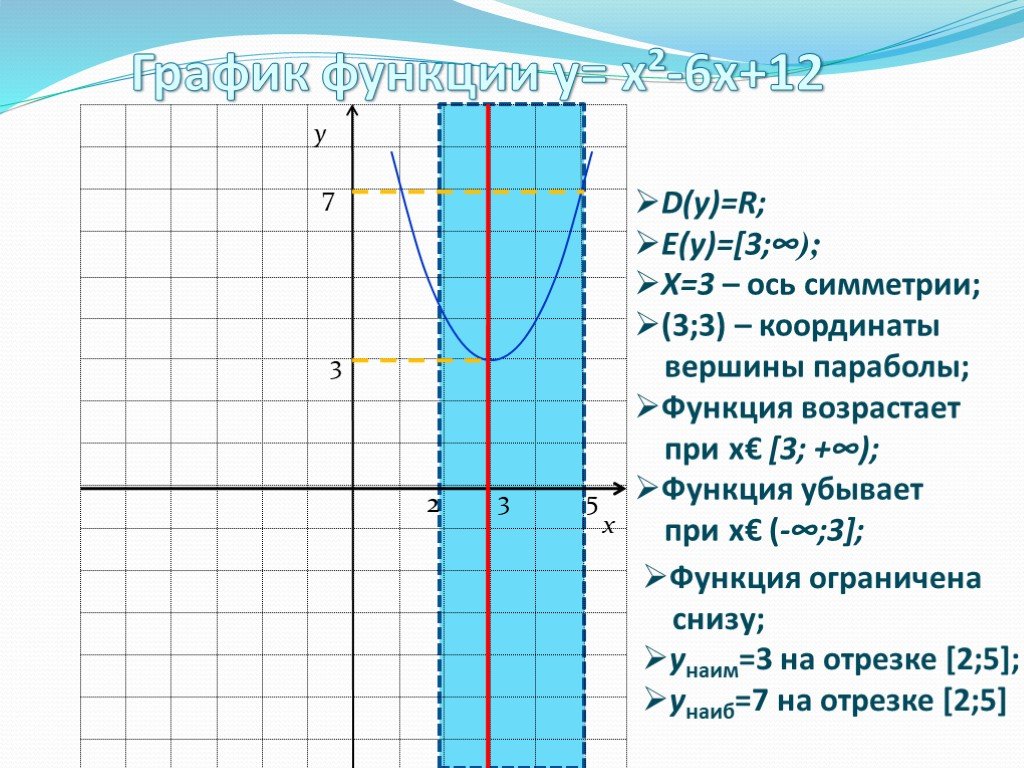
![D(y)=R; E(y)=[3;∞); X=3 – ось симметрии; (3;3) – координаты вершины параболы; Функция возрастает при х€ [3; +∞); Функция убывает при х€ (-∞;3]; Функция ограничена снизу; унаим=3 на отрезке [2;5]; унаиб=7 на отрезке [2;5]. 3 7 5 2 D(y)=R; E(y)=[3;∞); X=3 – ось симметрии; (3;3) – координаты вершины параболы; Функция возрастает при х€ [3; +∞); Функция убывает при х€ (-∞;3]; Функция ограничена снизу; унаим=3 на отрезке [2;5]; унаиб=7 на отрезке [2;5]. 3 7 5 2](https://prezentacii.org/upload/cloud/19/08/158204/images/thumbs/screen21.jpg)