Презентация "Круглые геометрические тела" по математике – проект, доклад
Презентацию на тему "Круглые геометрические тела" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрические тела и плоские фигуры
Алгоритм работы. 1. Задание 1. Кроссворд ( думай, отгадывай, составляй). Слайд 3-11. 2. Задание 2. Начерти в тетради. Слайд 13. 3. Задание 3. Найди ...Круглые тела
Обобщение и углубление знаний о круглых телах; применение их (круглых тел) на практике в повседневной жизни; Развитие логического мышления, творческой ...Геометрические тела вращения
МОУ Степановская СОШ. Костромская область Галичский район Д. Степаново Ул. Центральная д.10 Учитель: Елесина Галина Витальевна. Цели и задачи. Повторить ...Геометрические тела и их изображение
Что такое плоскость? Плоскость – это ровная, гладкая поверхность, имеющая два измерения. Плоскостей, расположенных в разных положениях, существует ...Геометрические тела в архитектуре г.Севастополя
Задание. Целью нашего исследования было в рамках программы реставрации набережной Балаклавы, найти здание, имеющее характерную форму геометрического ...Геометрические тела вокруг нас
Цели и задачи. Формирование комплексного видения проблемы и ее решения Формирование навыков работы с информацией: поиск информации, ее творческая ...Геометрические тела
Company Logo www.themegallery.com. Сфера Цилиндр Параллелепипед Куб Конус Пирамида Призма. Сфера. Замкнутая поверхность, геометрическое место точек ...Геометрические тела
КОГДА РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ ИЗМЕРЯЕТСЯ ПО ДУГЕ? На плоскости расстояние между двумя точками измеряется по прямой. На поверхности шара расстояние ...Геометрическая экскурсия по теме "Круглые тела в архитектуре"
Павловское начато строиться в 1777 году. Круг в Древней Греции считался венцом совершенства. Возможно, для того чтобы подчеркнуть совершенство природы ...Геометрические тела и окружающий мир
Окружающие предметы. Имеют форму куба. Изображение куба. Окружающие сооружения и предметы. Имеют форму пирамиды. Изображение треугольной пирамиды. ...Начальные геометрические понятия
ПРАВИЛЬНО, ПОДВОДИТЬ ИТОГИ! ОБОБЩЕНИЕ ПРОЙДЕННОГО МАТЕРИАЛА. КАКОЙ ТЕМОЙ МЫ ЗАНИМАЛИСЬ ВСЮ ВТОРУЮ ЧЕТВЕРТЬ? ПРАВИЛЬНО, ГЕОМЕТРИЧЕСКИМИ ФИГУРАМИ. . ...Вращательные движение твердого тела
Введение. Вращательным движением твёрдого тела или системы тел называется такое движение, при котором все точки движутся по окружностям, центры которых ...Плоские геометрические фигуры
ЗАГАДКА. Нет углов у меня, И похож на блюдце я, На тарелку и на крышку, На кольцо, на колесо. Кто же я такой, друзья? Он давно знаком со мной. Каждый ...Платоновы тела – ключ к устройству Земли и Мироздания
Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из двенадцати кусков кожи... Платон, "Федон". Этюд первый. Сферическая сковорода. Представление ...Вычислить объём тела вращения
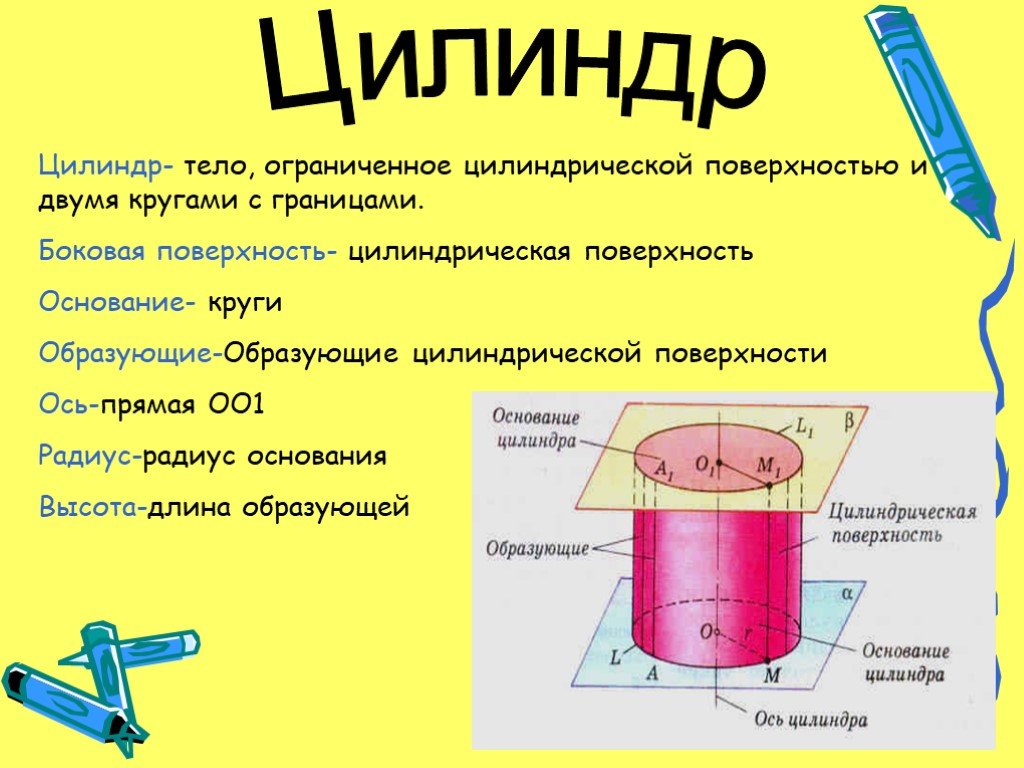
ОПРЕДЕЛЕНИЕ ЦИЛИНДРА. Цили́ндр (др.-греч. κύλινδρος — валик, каток) Цилиндр - тело, ограниченное цилиндрической поверхностью и двумя кругами с границами ...Начальные геометрические сведения. Перпендикулярные прямы
Цели:. Повторить понятие перпендикулярные прямые; Рассмотреть свойство перпендикулярных прямых; Применять полученные знания при решении задач. Вспомним! ...Начальные геометрические сведения
Знак «+» правильные утверждения знак «-» ошибочные. 1. Примерами геометрических фигур на плоскости являются точка, прямая, квадрат, куб , шар. 2. ...Начальные геометрические сведения
I.Точки, прямые, отрезки. 1. Взаимное расположение точек и прямых. «точка А лежит на прямой а»: А а «точка В не лежит на прямой а»: В а. 2.Свойства ...Начальные геометрические сведения
В переводе с греческого слово «геометрия» означает «землемерие» «гео» - по-гречески земля, «метрео» - мерить. Геометрия изучает свойства геометрических ...Объём тела
ρ масса плотность кг с время t m м/с путь скорость инерция v км/ч год г м мин s. . . . . . Архимед. Архиме́д (Ἀρχιμήδης; 287 до н. э.) — 212 до н. ...Конспекты
Круглые тела
Методика проведения урока-обобщения по теме: "Круглые тела" (фигуры вращения). ПЛАН ОТКРЫТОГО УРОКА. Тема:. Фигуры вращения. Тип урока:. Урок ...Формулы пути и массы тела как примеры прямой пропорциональности
Конспект урока алгебры в 7 классе. Автор:. . Елизарова Инна Ивановна. Место работы:. МБОУ «Чудиновская основная общеобразовательная школа ...Фигуры и тела вращения
Урок геометрии в 11 классе по теме «Фигуры и тела вращения». «Предмет математики настолько серьёзен, что надо. не упускать возможности. ...Решение задач на тела вращения
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ГИМНАЗИЯ №40» г. БАРНАУЛА. МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА. «Современные ...Простейшие геометрические понятия
Емцева Юлия Ивановна. . Гимназия №33 г.Краснодара. . Учитель начальных классов. . . Урок математики в 1 классе. (здоровьесберегающие ...Начальные геометрические сведения
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Начальные геометрические сведения
Урок - обобщение геометрии по теме «Начальные геометрические сведения». . . Учитель: Козлова Евгения Николаевна. Цели урока:. Повторение, закрепление ...Начальные геометрические сведения
Тема: Начальные геометрические сведения. Цель:. систематизировать знания учащихся об основных свойствах простейших геометрических фигур. Задачи:. ...Начальные геометрические сведения
Конспект урока на тему. «Начальные геометрические сведения». Составила: Учитель математики. МКОУ « Москаленский лицей» Бадюк Ольга Ярославна. ...Многогранники и тела вращения. Их площади и объемы
Урок геометрии 11 класс «Многогранники и тела вращения. Их площади и объемы» на основе метода проектов. График работы над проектом:. Подготовительный ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 декабря 2018
Категория:Математика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию