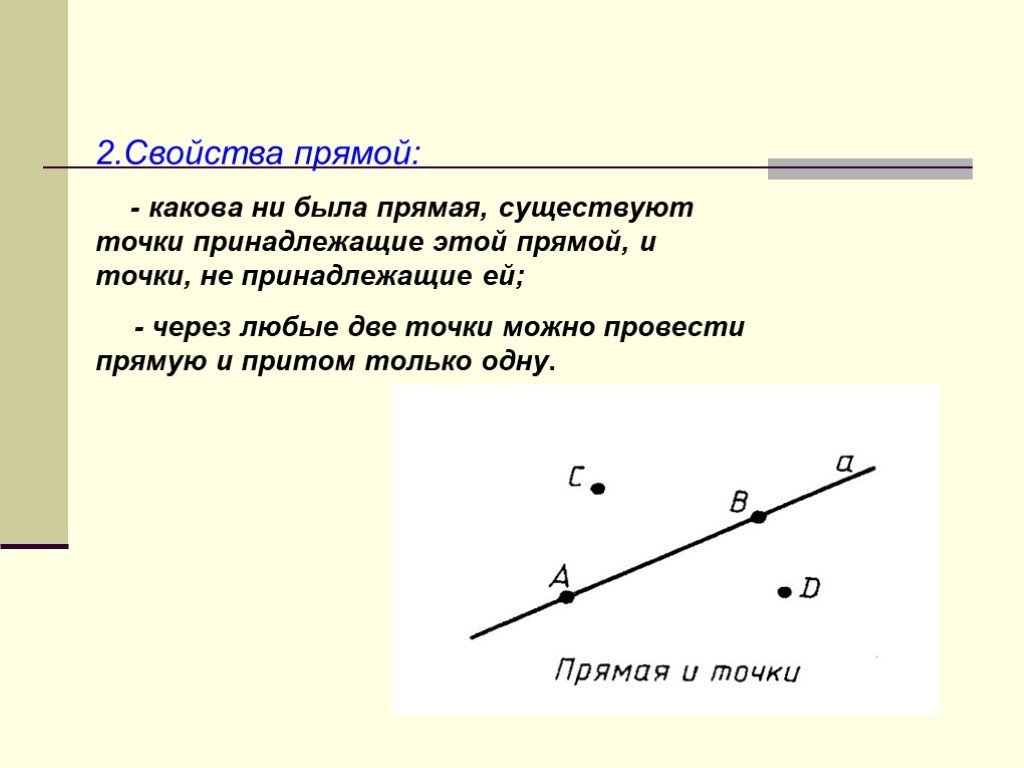
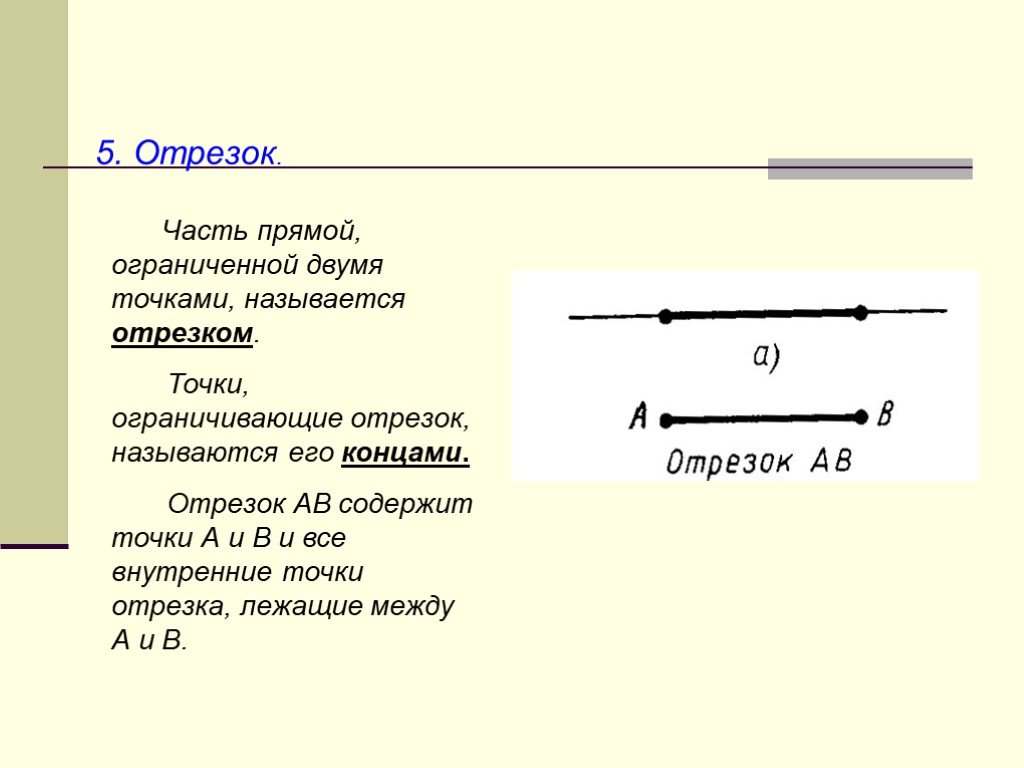
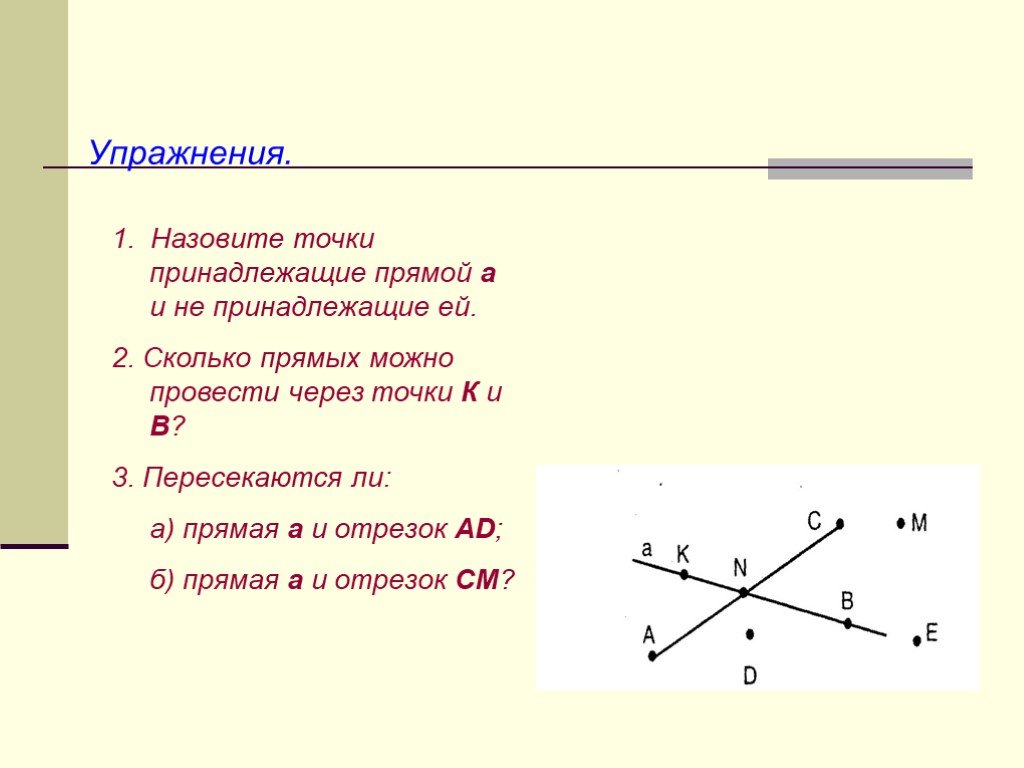
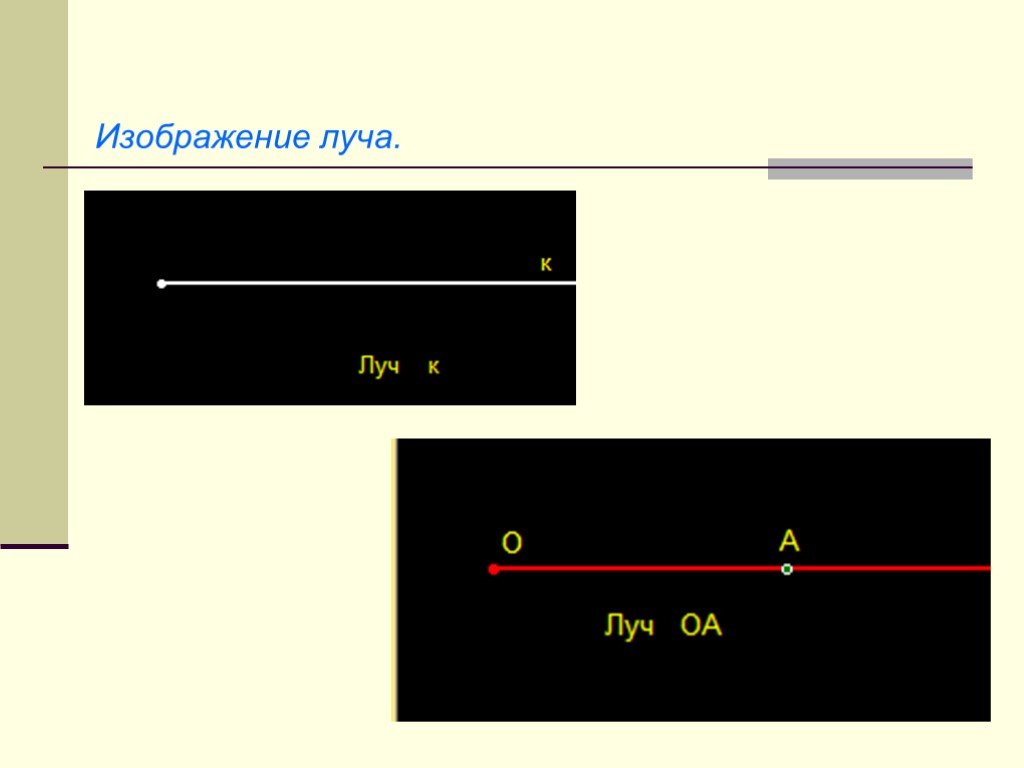
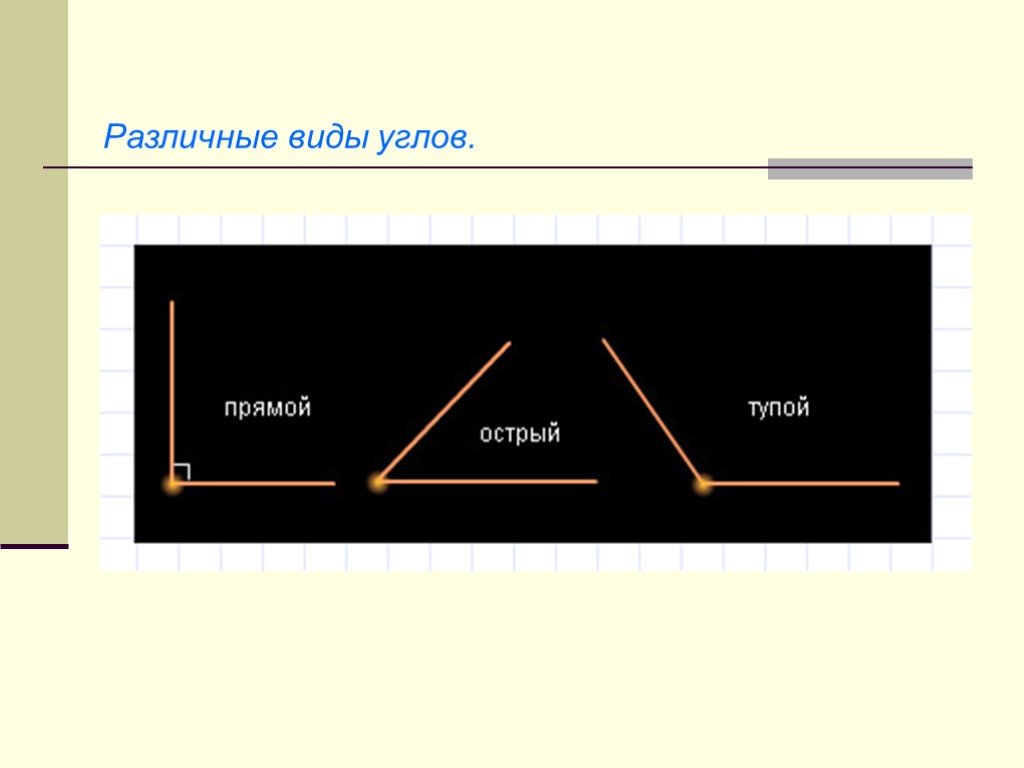
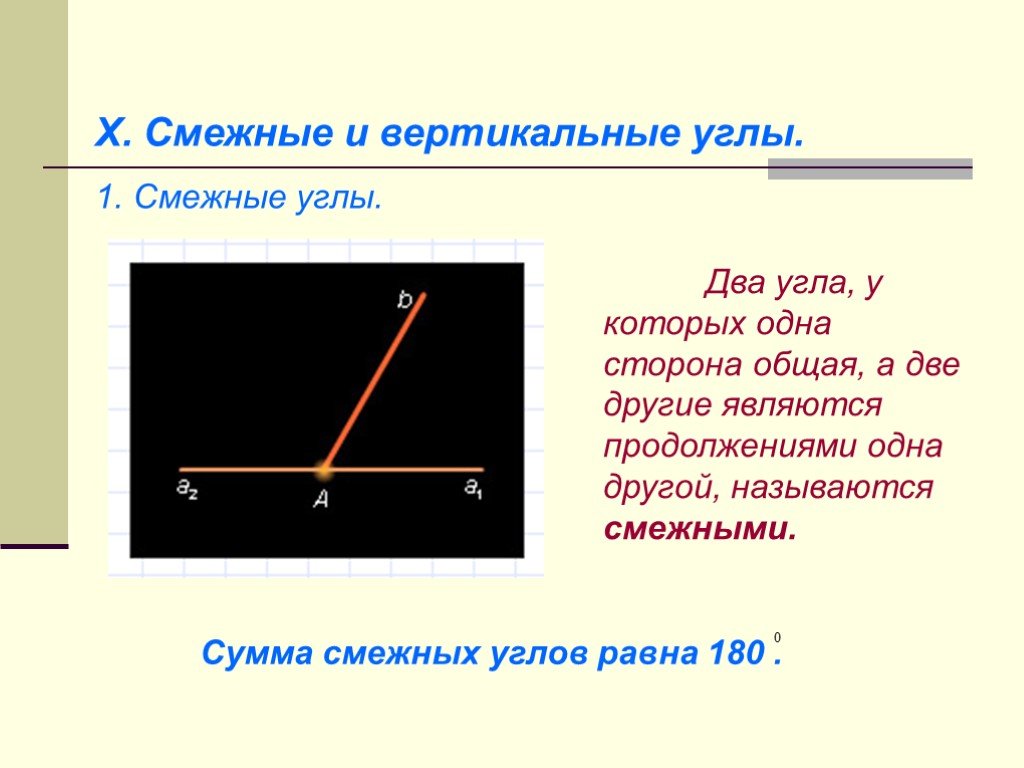
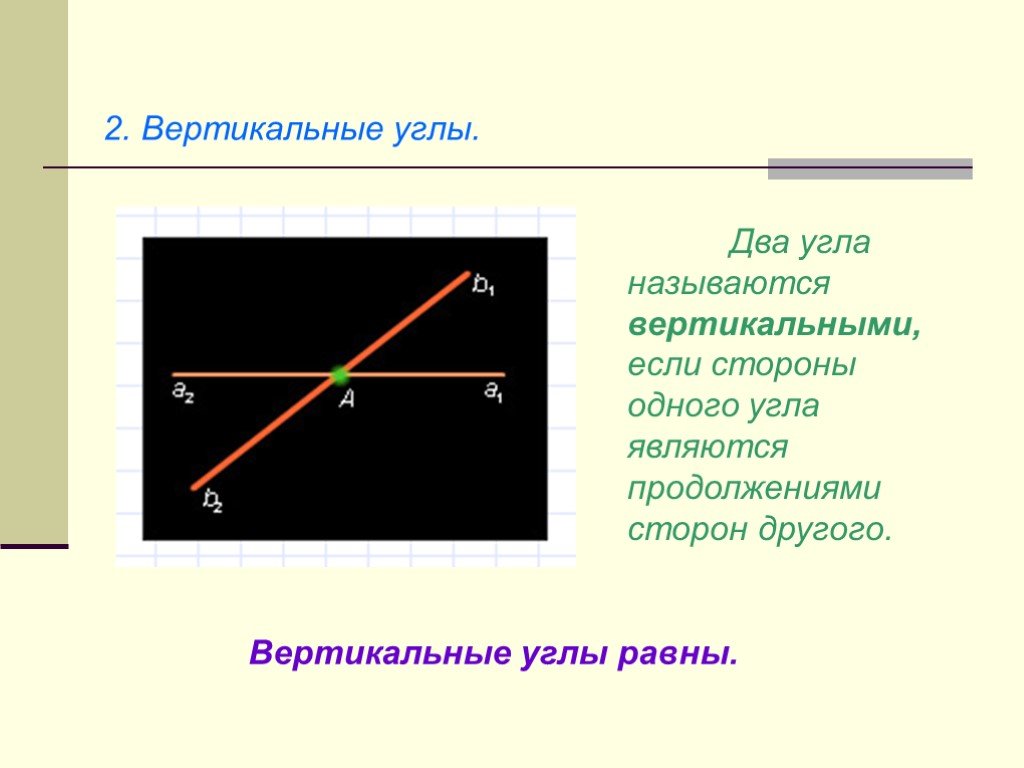
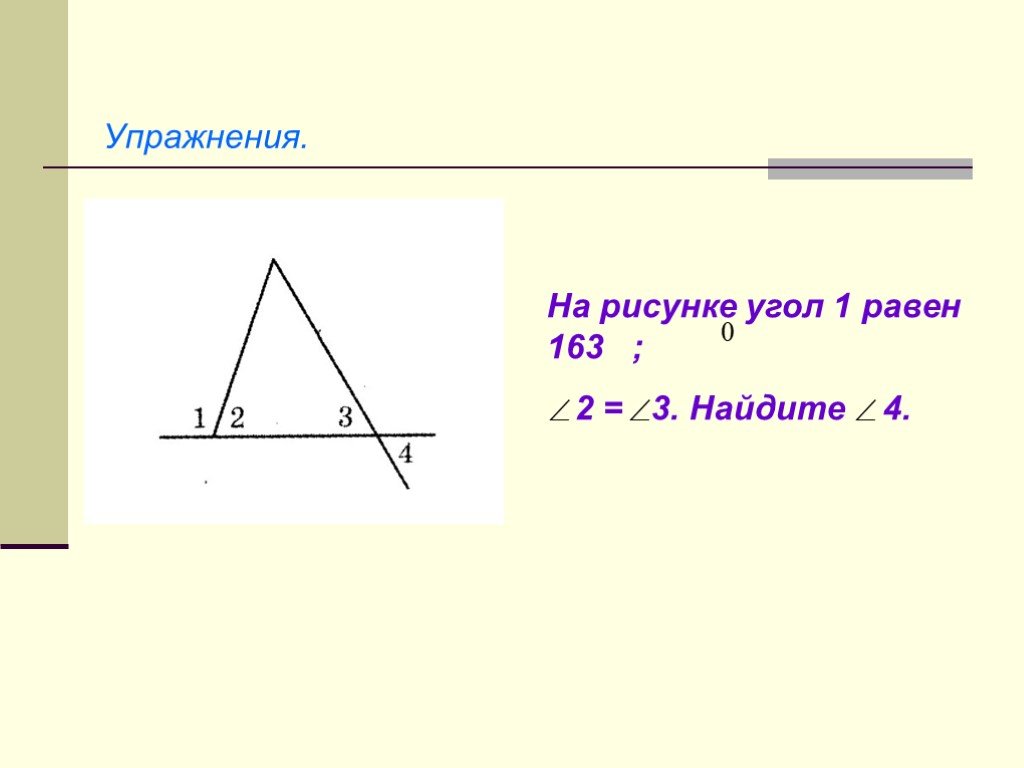
Презентация "Начальные геометрические сведения" (7 класс) по математике – проект, доклад
Презентацию на тему "Начальные геометрические сведения" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
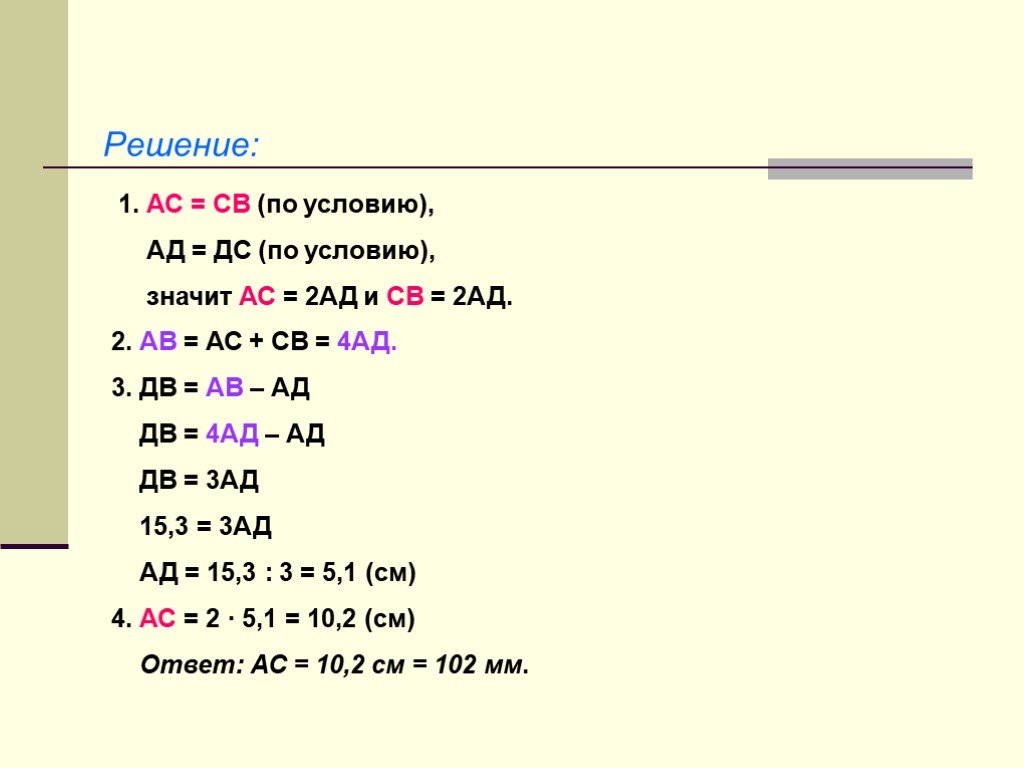
Слайды презентации
Список похожих презентаций
Начальные геометрические сведения. Перпендикулярные прямы
Цели:. Повторить понятие перпендикулярные прямые; Рассмотреть свойство перпендикулярных прямых; Применять полученные знания при решении задач. Вспомним! ...Начальные геометрические сведения
Знак «+» правильные утверждения знак «-» ошибочные. 1. Примерами геометрических фигур на плоскости являются точка, прямая, квадрат, куб , шар. 2. ...Начальные геометрические сведения
Тема урока:. Что изучает геометрия? 2. Что означает слово «геометрия»? 3. Когда и как зародилась наука «геометрия»? 4. Какие геометрические фигуры ...Начальные геометрические сведения
В переводе с греческого слово «геометрия» означает «землемерие» «гео» - по-гречески земля, «метрео» - мерить. Геометрия изучает свойства геометрических ...Начальные сведения из стереометрии
Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве. ТЕТРАЭДР -. МНОГОГРАННИК, СОСТАВЛЕННЫЙ ИЗ 4 ТРЕУГОЛЬНИКОВ. Правильный ...Начальные геометрические сведенья
а В А. Начертите прямую. Как её можно обозначить? Построение. О. Начертите прямые, пересекающиеся в точке О. С D. b. Используя рисунок и символы принадлежности, ...Начальные геометрические понятия
ПРАВИЛЬНО, ПОДВОДИТЬ ИТОГИ! ОБОБЩЕНИЕ ПРОЙДЕННОГО МАТЕРИАЛА. КАКОЙ ТЕМОЙ МЫ ЗАНИМАЛИСЬ ВСЮ ВТОРУЮ ЧЕТВЕРТЬ? ПРАВИЛЬНО, ГЕОМЕТРИЧЕСКИМИ ФИГУРАМИ. . ...Объёмные геометрические фигуры
Ребята! Предлагаем вам познакомиться с объёмными геометрическими фигурами и предметами, которые на них похожи. Вспомните, что вас окружает, и приведите ...Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Вводная беседа. Геометрия в переводе с греческого «землемерие» («гео»- по-гречески земля, а «метрео» - мерить). Первым, кто начал получать геометрические ...Начальные понятия геометрии
Урок введение в геометрию. Как возникла геометрия? Что изучает геометрия? Начальные геометрические сведения. Практическое проведение прямых. « Вдохновение ...Круглые геометрические тела
Содержание. Цилиндр Конус Сфера Исторические факты Это интересно Авторы. Цилиндр. Цилиндр- тело, ограниченное цилиндрической поверхностью и двумя ...Плоские геометрические фигуры
ЗАГАДКА. Нет углов у меня, И похож на блюдце я, На тарелку и на крышку, На кольцо, на колесо. Кто же я такой, друзья? Он давно знаком со мной. Каждый ...Цилиндр: основные сведения
Тело, образованное путём вращения прямоугольника вокруг одной из его сторон, как оси называется цилиндром. В основаниях – два равных круга. Отрезки, ...Арифметические и геометрические прогрессии
«Гений состоит из 1 процента вдохновения и 99 процентов потения» Т. Эдисон ПЛАН УРОКА: 1. Мотивационное начало (работа с таблицей); 2. Сообщение цели ...Какие они разные - эти геометрические фигуры
показать отличие и сходство прямоугольника и квадрата, сформировать навык определения фигур по сторонам и углам, учить строить фигуры с помощью линейки ...Построение сечений многогранников геометрия
Обучающая цель: формирование умений и навыков построения сечений. Развивающая цель: формирование и развитие у учащихся пространственного представления. ...Поворот и геометрия
ВСПОМИНАЕМ. Что называют параллельным переносом на заданный вектор? На что при параллельном переносе отображается прямая? Является ли параллельный ...Перпендикулярность в пространстве геометрия
Цель:. Познакомиться с перпендикулярностью в пространстве. Проанализировать различные источники по данной теме. Выделить основные подходы к рассмотрению ...Неевклидова геометрия
Мы выбрали эту тему так как она нас очень заинтересовала тем , что геометрия Лобачевского очень полезна в современном мире, и мы хотим немного рассказать ...Небесная геометрия
Цели и задачи. Цель: дать физическое и математическое обоснование разнообразия форм снежинок. Задачи: изучить историю появления фотографий с изображениями ...Конспекты
Начальные геометрические сведения
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Начальные геометрические сведения
Урок - обобщение геометрии по теме «Начальные геометрические сведения». . . Учитель: Козлова Евгения Николаевна. Цели урока:. Повторение, закрепление ...Начальные геометрические сведения
Тема: Начальные геометрические сведения. Цель:. систематизировать знания учащихся об основных свойствах простейших геометрических фигур. Задачи:. ...Начальные геометрические сведения
Конспект урока на тему. «Начальные геометрические сведения». Составила: Учитель математики. МКОУ « Москаленский лицей» Бадюк Ольга Ярославна. ...История возникновения и развития геометрии. Начальные геометрические сведения
Урок геометрии с использованием ИКТ. . Класс:. 7. Учитель:. Петрова Марина Николаевна,. учитель математики МБОУ СОШ №76. . Орджоникидзевского ...Начальные сведения из планиметрии
Методическая разработка урока по геометрии и английскому языку для учащихся 7 класса учителя математики Засыпкиной Е.В. Тема урока:. Начальные ...Простейшие геометрические понятия
Емцева Юлия Ивановна. . Гимназия №33 г.Краснодара. . Учитель начальных классов. . . Урок математики в 1 классе. (здоровьесберегающие ...Первые сведения о статистике. Выборка. Гистограмма. Среднее значение, мода и медиана выборки. Решение упражнений
Тема урока: Первые сведения о статистике. Выборка. Гистограмма. Среднее значение, мода и медиана выборки. Решение упражнений. Цели:Обучающая: формирование ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 декабря 2018
Категория:Математика
Классы:
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию