Конспект урока «Теорема Виета» по математике
Астахова И.А. , учитель математики ТОГБОУ кадетская школа-интернат «Многопрофильный кадетский корпус», Г.Тамбов
Тема урока: «Теорема Виета»
Цели урока: Формирование устойчивых умений и навыков применения теоремы Виета и обратной к ней для решения некоторых классов задач: нахождение суммы и произведения корней квадратного уравнения, исследование знаков его корней, отыскание корней приведённого квадратного уравнения подбором, составление квадратного уравнения с заданными корнями и т. д. Показать учащимся преимущества использования вышеназванных теорем.
Тип урока: практикум.
Ход урока:
Оргмомент
Сообщение темы и целей урока, видов и форм работы. (Сегодня на уроке мы вспомним условия применения теоремы Виета, для решения каких задач она используется, упрощает ли решение квадратных уравнений и их проверку или удобнее действовать обычными способами: находить корни уравнения по изученным формулам, а проверку выполнять по определению корня уравнения).
Актуализация знаний и устные упражнения
Каковы условия применения теоремы Виета? (Теорема Виета применима к приведённому квадратному уравнению, имеющему корни). Сформулируйте теорему Виета. Для каких целей она используется? (Теорема Виета используется для нахождения суммы ипроизведения корней квадратного уравнения, для проверки правильности его решения, для исследования знаков корней квадратного уравнения). Сформулируйте теорему, обратную теореме Виета. Для чего она применяется? (Теорема, обратная теореме Виета, используется для составления квадратных уравненийй с заданными корнями и для решения приведенного квадратного уравнения методом подбора).
1.Найдите сумму и произведение корней уравнения, не решая его.
| x2+6x-5=0 | 2x2-9x+5=0 | 3x2-14x-5=0 | |
| x1+x2 | -6 | 9/2 | 14/3 |
| x1x2 | -5 | 5/2 | -5/3 |
2.Можно ли утверждать, что оба корня уравнения x2-8x-9=0 положительны? (Нет, так как произведение корней отрицательно). Можно ли утверждать,что модуль отрицательного корня больше? (Нет, так как сумма корней положительна). Внесите изменение в уравнение так, чтобы модуль отрицательного корня был больше) (x2+8x-9=0).
Итак, как мы можем узнать, одинаковых ли знаков корни уравнения? (Если свободный член уравнения положительное число, то корни уравнения одинаковых знаков, если отрицательное –противоположных знаков). Если корни уравнения одинаковых знаков, как определить какой именно это знак? (В этом случае оба корня уравнения будут иметь знак, противоположный второму коэффициенту уравнения).
3.Если каждый корень приведенного квадратного уравнения увеличить вдвое ( втрое), как изменятся его коэффициенты? (Второй коэффициент увеличится в два (в три) раза, а свободный член - в четыре (в девять) раз.
4.Известен один из корней уравнений, найдите второй двумя способами: a) x2+6x-40=0, x1=-10; б) 13x2-11x+2=0, x1=5.
5.Найдите подбором корни приведенного квадратного уравнения:
x2+8x+7=0,
x2-7x+12=0,
x2+2x-15=0,
x2-2x-3=0.
Выполнение упражнений
1.Составить приведенное квадратное уравнение с заданными корнями. (Решение вносится в заранее записанную на доске таблицу. Учащиеся выходят к доске «по цепочке» и комментируют свое решение).
-
x1
x2
уравнение
5
-2
x2-3x-10=0
-3
-1
x2+4x+3=0
3
1
x2-4x+3=0
-2
5
x2+3x-10=0
2.Один из корней уравнений равен –3.Найдите второй корень и коэффициент k: a) x2+kx+18=0, б) x2-5x+k=0 (Двое учащихся работают за закрытой доской, на местах-работа в парах, затем следует фронтальная проверка решения).
3
 .Составьте приведенное квадратное уравнение, зная один корень, а затем найдите второй корень. (Учащиеся работают на местах самостоятельно, а затем несколько решений выносится на доску, например: ( x1=5 ) ( 52+3*5-40=0) (x2+3x-40=0) ( x2=-8 ).
.Составьте приведенное квадратное уравнение, зная один корень, а затем найдите второй корень. (Учащиеся работают на местах самостоятельно, а затем несколько решений выносится на доску, например: ( x1=5 ) ( 52+3*5-40=0) (x2+3x-40=0) ( x2=-8 ).
4.Составьте задачу по уравнению x2+2x-120=0. Можно предварительно уравнение преобразовать: x*(x-2)=120. (Выслушиваются задачи, одна из них решается у доски алгебраическим способом. Длина прямоугольника на 2 см. больше его длины. Найдите длины сторон прямоугольника, если его площадь равна 120 см2).
5.Решить уравнение y2+17y+60=0, выполнить проверку двумя способами: обычным и с использованием теоремы Виета и обратной к ней. (Двое учащихся работают у доски). Если сравним время, затраченное на решение и количество выполненных операций, то преимущество использования теоремы Виета и обратной к ней становится очевидным. Это становится особенно актуальным на уроках алгебры и геометри в старших классах, так как многие задачи сводятся к решению приведенного квадратного уравнения и необходимость решать такие уравнения возникаете несколько раз за урок.
6.В курсе школьной математики изучется теорема Виета для приведённого уравнения второй степени, т.е. когда в левой части уравнения стоит многочлен второй степени. Но теорема справедлива и для произвольного приведённого многочлена. Сколько корней может иметь уравнение второй (третьей, четвёртой) степени? (Уравнение второй (третьей, четвёртой) степени может иметь не более двух (трёх, четырёх) корней. Соотношение между корнями и коэффициентами уравнения выводится с использованием разложения многочлена, стоящего в левой части уравнения на множители. Проанализируйте следующие записи и найдите связь между корнями и коэффициентами приведённого уравнения четвёртой степени.
x2+px+q=(x-x1)(x-x2)=x2-x2x-x1x+x1x2=x2-(x1+x2)x+(x1x2),
x2+px+q=0,
p=-(x1+x2),
q=x1x2 ;
x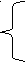 3+px2+qx+r=0,
3+px2+qx+r=0,
p=-(x1+x2+x3),
q=x1x2+x2x3+x1x3,
r=-x1x2x3 ;
x4+px3+qx2+rx+s=0,
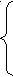 p=-(x1+x2+x3+x4),
p=-(x1+x2+x3+x4),
q=x1x2+x1x3+x1x4+x2x3+x2x4+x3x4,
r=-(x1x2x3+x1x2x4+x2x3x4),
s=x1x2x3x4).
Задание на дом
1.Составить и решить задачу по уравнению ( x-3)*(x-7)=21.
2. (необязательное задание) а) Составить уравнение третьей степени с корнями, равными 1, 2, -1.б) Составить уравнение четвёртой степени , два корня которого равны 2 и два равны –2.
Итоги урока
Чем занимались на уроке? Нужно ли уметь пользоваться прямой и обратной теоремами Виета и почему?Что понравилось на уроке, а что нет?
Здесь представлен конспект к уроку на тему «Теорема Виета», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

