Конспект урока «Решение квадратных уравнений» по математике
"Решение квадратных уравнений"
![]()
![]()
![]()
![]()
![]() Цели урока:
Цели урока:
образовательные: обобщение и систематизация основных знаний и умений по теме: «Квадратные уравнения»;
развивающие: развитие логического мышления, познавательного интереса учащихся, памяти, внимания, общеучебных умений, умения обобщать, сравнивать, делать выводы;
воспитательные: воспитание трудолюбия, взаимопомощи, взаимоуважения и математической культуры.
Ход урока.
Здравствуйте, ребята. Нам предстоит поработать над очень важной темой: “Решение квадратных уравнений”. Вы уже достаточно знаете и умеете по этой теме, поэтому наша с вами задача: обобщить и сложить в систему все те знания и умения, которыми вы владеете.
А законы у нас сегодня будут такие: каждый из вас имеет возможность получить оценку за урок по результатам работы на различных его этапах. Для этого у вас на партах лежат карты результативности, в которые вы будете фиксировать свои успех в баллах
Оценочный лист
Ф. И._____________________
| Наличие ДЗ | Устный счет | Диктант | Тест | «Лови ошибку» | Решение уравнений | ИТОГ | |
| Оценка | |
|
|
|
|
|
|
Приступим к работе.
Попрошу открыть тетради, записать число и тему сегодняшнего урока.
“Решение квадратных уравнений”.
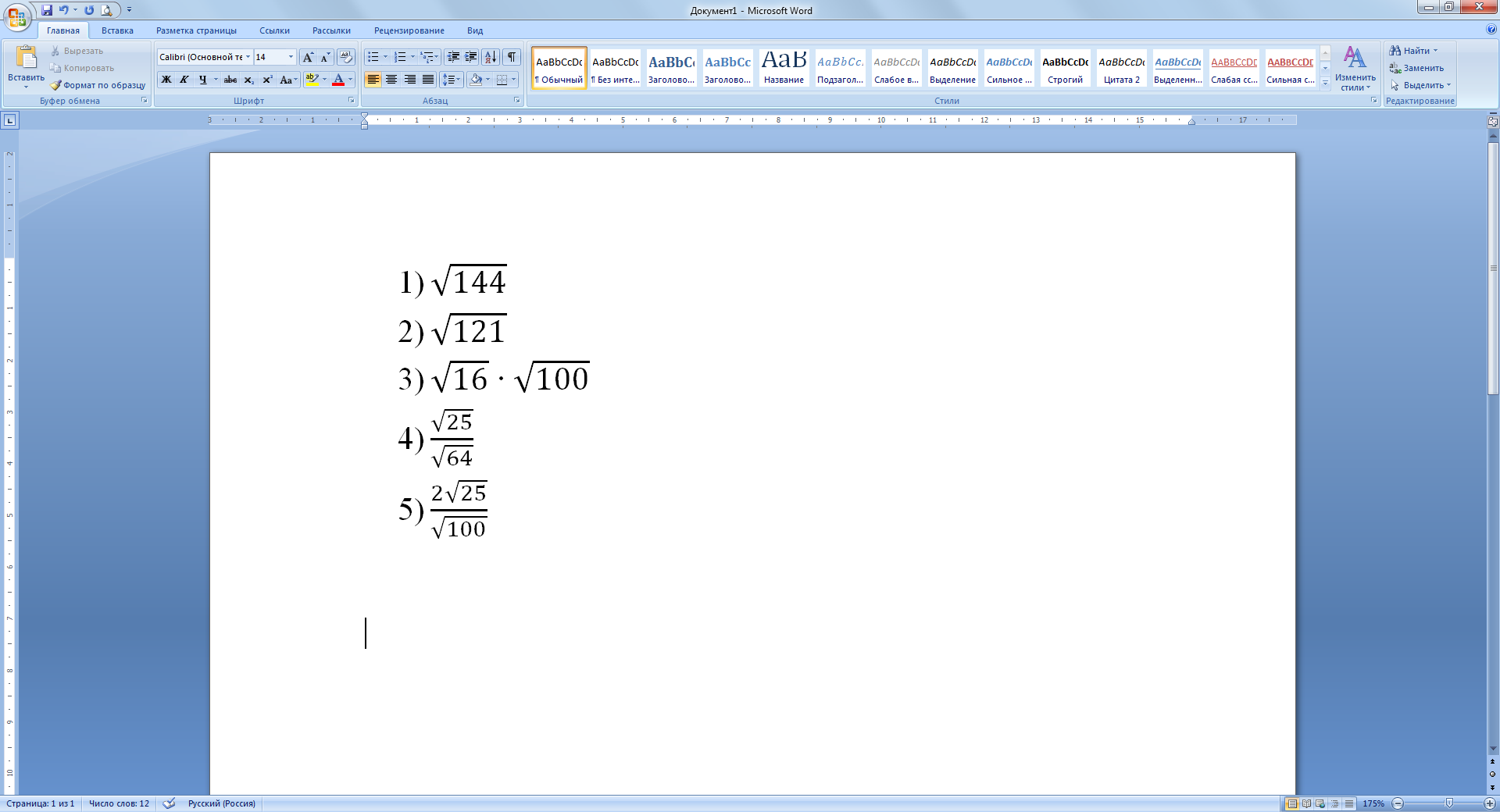
Проверяем:
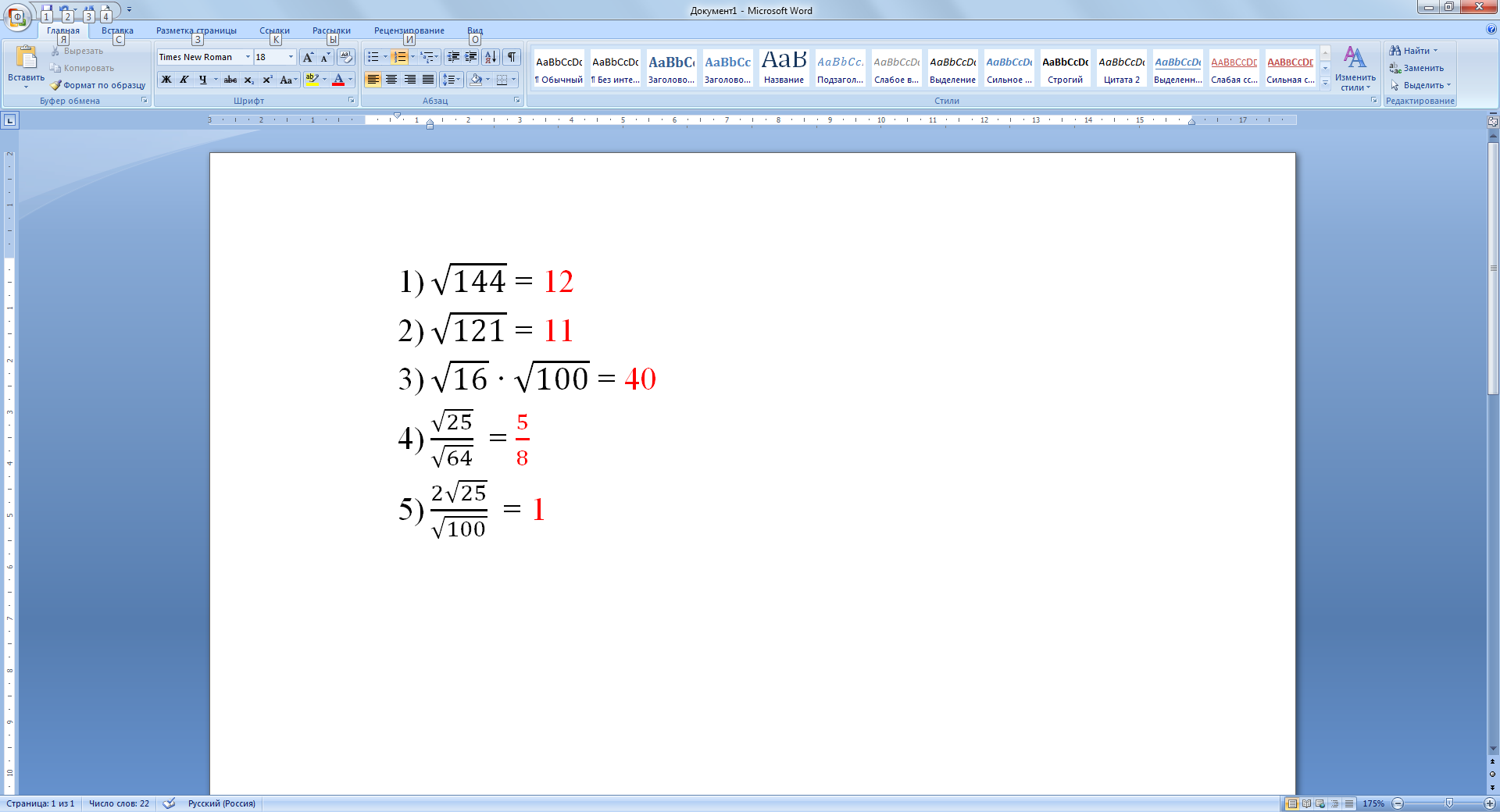
Критерии оценивания:
1 ошибка – «4»
2 ошибки – «3»
3 ошибки и более – «2»
Диктант:
Вариант 1
1) Запишите квадратное уравнение, у которого первый коэффициент 3, второй коэффициент -5, свободный член 0.
Ответ: 3х2 – 5х = 0
2) Запишите приведенное квадратное уравнение, у которого
второй коэффициент и свободный член равны -2.
Ответ: х2 - 2х - 2 = 0
3) Вычислите дискриминант квадратного уравнения х2 - 5х + 6 = 0
Ответ: Д = (-5)2 – 4 ∙ 1 ∙ 6 = 25 – 24 = 1
4)Запишите, чему равны сумма и произведение корней квадратного уравнения х2 - 5х + 6 = 0.
Ответ: х1 + х2 = 5,
х1 ∙ х2 = 6.
5) Сколько корней имеет квадратное уравнение, если Д
Ответ: корней нет.
Вариант 2
-
Запишите квадратное уравнение, у которого первый коэффициент -5, второй коэффициент 3, свободный член 0.
Ответ: -5х2 + 3х = 0
2) Запишите приведенное квадратное уравнение, у которого
второй коэффициент и свободный член равны -3.
Ответ: х2 - 3х - 3 = 0
3) Вычислите дискриминант квадратного уравнения 3х2 + 2х – 1 = 0
Ответ: Д = 22 – 4 ∙ 3 ∙ (-1) = 4 + 12 = 16
4) Запишите, чему равны сумма и произведение корней квадратного уравнения х2 - 6х + 5 = 0.
Ответ: х1 + х2 = 6,
х1 ∙ х2 = 5.
5) Сколько корней имеет квадратное уравнение, если Д > 0?
Ответ: 2 корня.
- Теперь давайте проверим, насколько хорошо вы умеете определять виды квадратных уравнений. Вашему вниманию предлагается тест, в котором записаны, пять уравнений. Напротив каждой колонки вы ставите плюс, если оно принадлежит к данному виду.
Тест “Виды квадратных уравнений”
| полное | неполное | приве- денное | неприве- денное | Общий балл | |
| 1. х2 + 8х+3 = 0 |
|
|
|
|
|
| 2. 6х2 + 9 = 0 |
|
|
|
| |
| 3. х2 – 3х = 0 |
|
|
|
| |
| 4. –х2 + 2х +4 = 0 |
|
|
|
| |
| 5. 3х + 6х2 + 7 =0 |
|
|
|
|
Критерий оценивания:
Нет ошибок – 5 б.
1 – 2 ош. – 4б.
3 - 4 ош. - 3б.
5 - 6 ош. – 2б.
Более 6 ош. – 0 б.
Ребята выполняют работу, а затем меняются листочками и по ключу проверяют ответы, оценивая работу товарища. Результат записывается в колонку “Общий балл”, а затем в “Карту результативности”.
Ключ к тесту:
| + |
| + |
| |
| 2. |
| + |
| + |
| 3. |
| + | + |
|
| 4. | + |
|
| + |
| 5. | + |
|
| + |
Следующее задание «Лови ошибку»
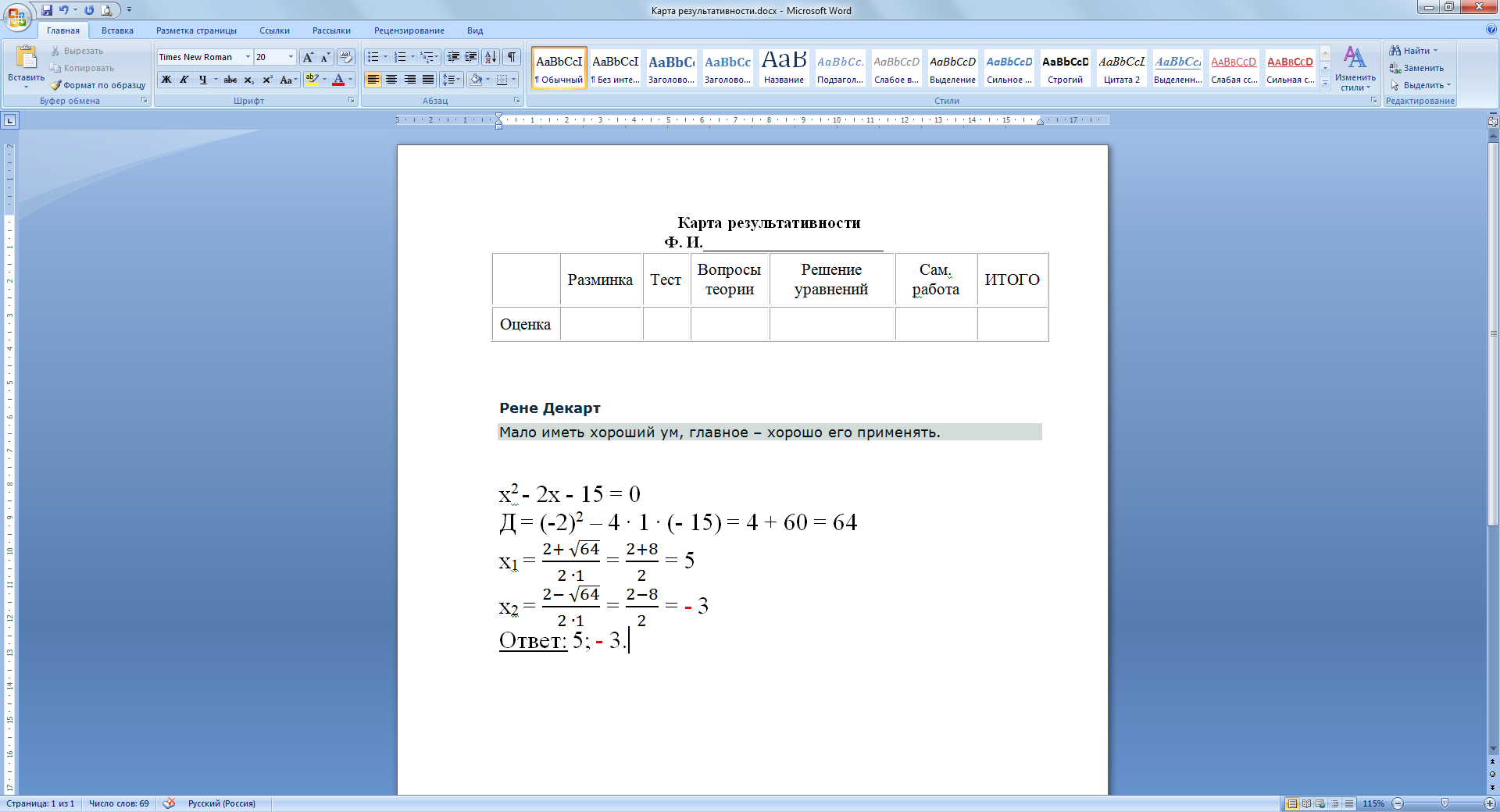
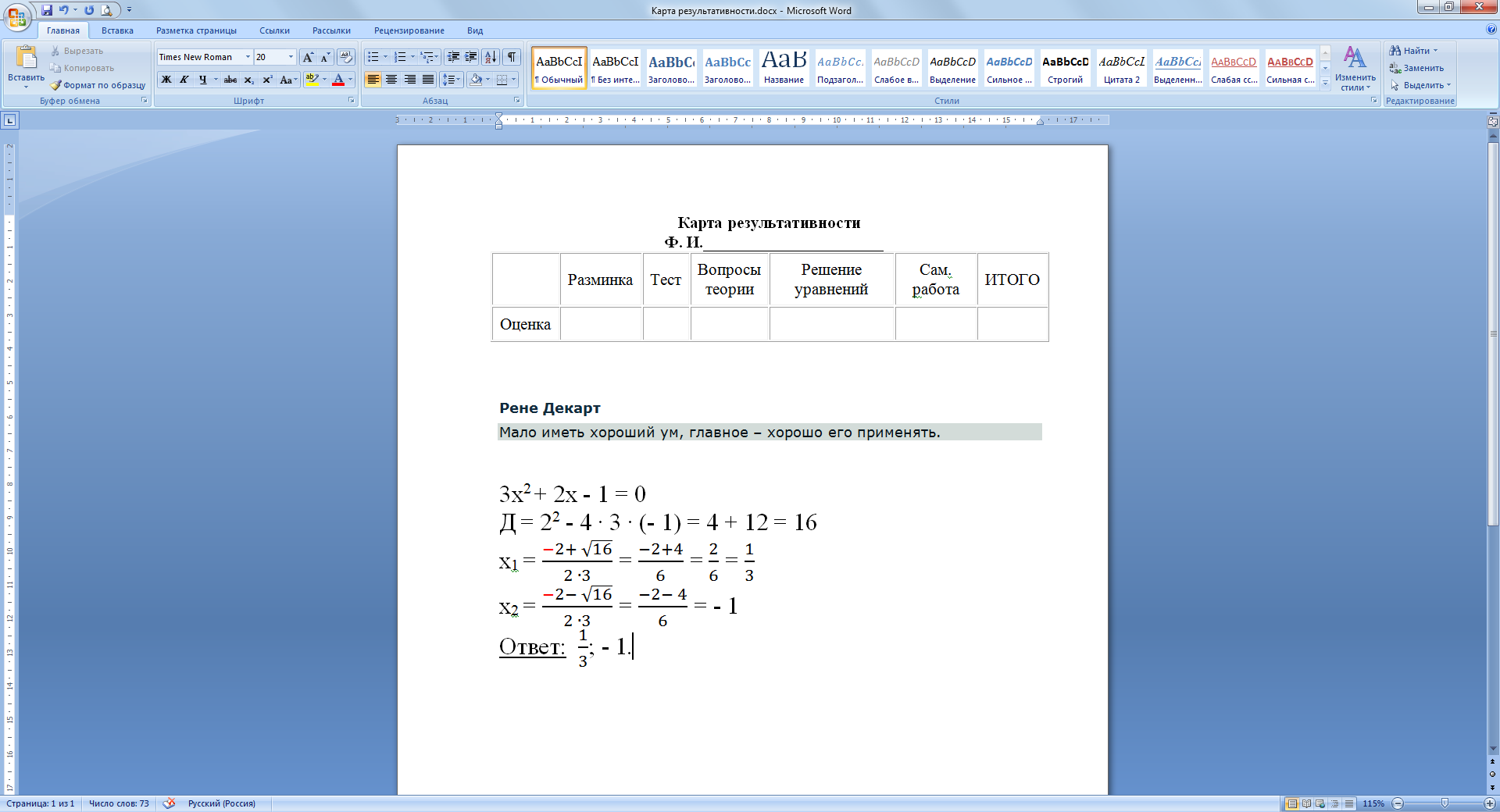
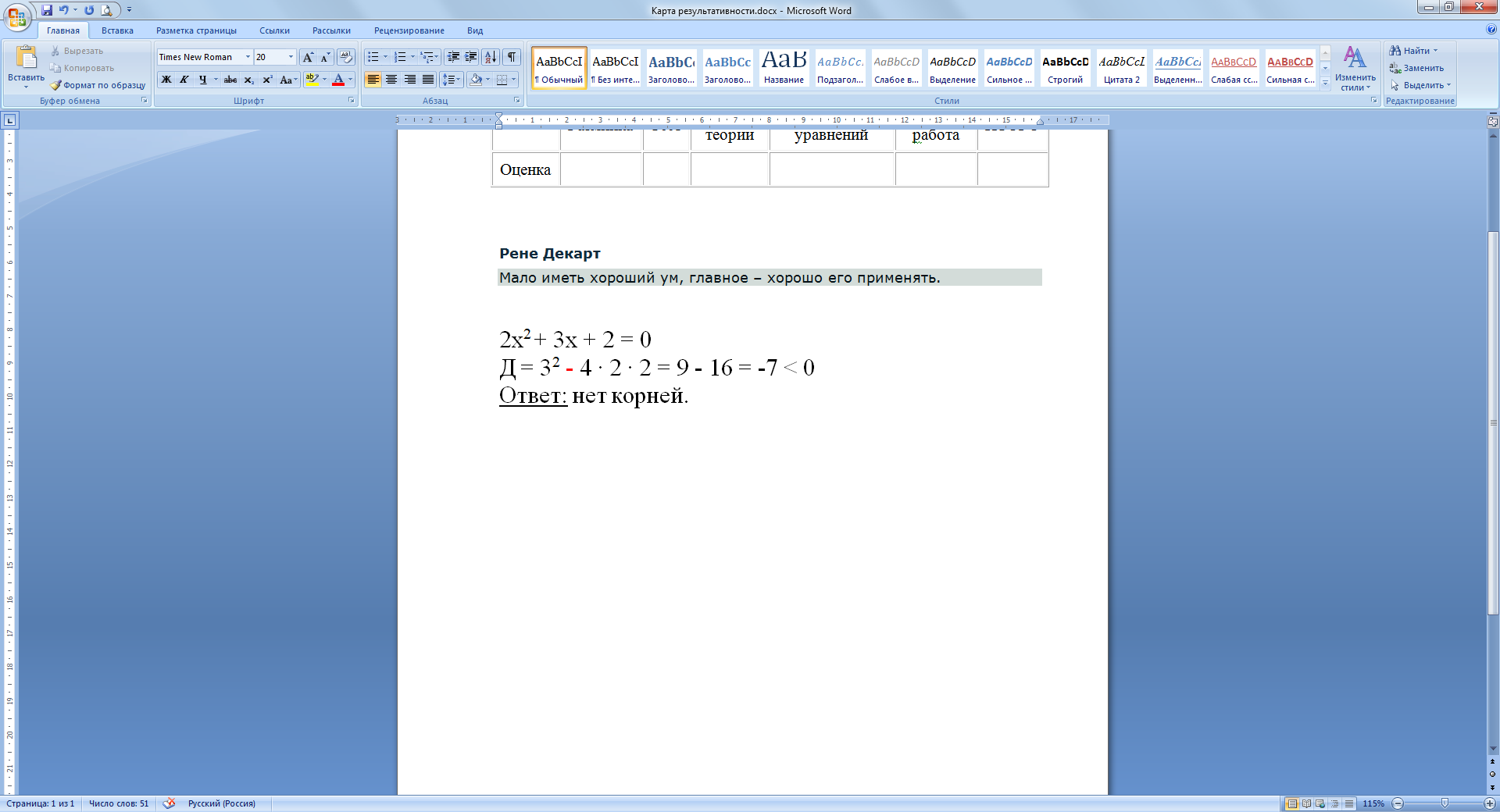
Ну что ж, приступим к практической части нашего урока.
«Математику уже затем учить надо, что она ум в порядок приводит»
М. В. Ломоносов
«Уравнения для меня важнее, потому что политика — для настоящего, а уравнения — для … (вечности)»
Альберт Эйнштейн
Перед вами список различных уравнений. Ваша задача отгадать, решив уравнения.
Решите уравнения:
-
х2 – 2х + 14 = 0;
-
х2 – 7х = - 10;
-
х2 – 7 = 6х;
-
х2 – 8х = 0;
-
х4 + 3х2 - 10 = 0.
Итог урока
- Итак, мы проделали большую работу. Вы старательно зарабатывали баллы, настало время подвести итог. Предлагаю закончить одну из фраз:
- сегодня на уроке я узнал…
- сегодня на уроке мое настроение…
- сегодня на уроке было…
Домашнее задание:
Задача 1: Площадь доски прямоугольной формы равна 4500 кв. см. Доску распилили на две части, одна из которых представляет собой квадрат, а другая – прямоугольник. Найдите сторону получившегося квадрата, если длина отпиленного прямоугольника равна 120 см.
Задача 2: В прямоугольном треугольнике один из катетов на 3 см меньше гипотенузы, а другой – на 6 см меньше гипотенузы. Найдите гипотенузу.
Здесь представлен конспект к уроку на тему «Решение квадратных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

