5-й класс. Математика. Урок «Площадь сложной фигуры».

Вовденко Ольга Леонидовна, учитель математики

МБОУ СОШ № 61 имени М.И. Неделина г.Липецк

Цели урока:

Образовательные:

• закрепление знаний формул площади прямоугольника, прямоугольного треугольника;

• анализ заданий на вычисление площади “сложной” фигуры и способов их выполнения;

• самостоятельное выполнение заданий для проверки знаний, умений, навыков.

Развивающие:

• развитие приёмов умственной и исследовательской деятельности;

• развитие умения слушать и объяснять ход решения.

Воспитательные:

• воспитывать у учащихся навыки учебного труда;

• воспитывать культуру устной и письменной математической речи;

• воспитывать дружеское отношение в классе и умение работать в группах.

Тип урока: комбинированный.

Оборудование:

1. Математика: учебник для 5 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов и др., М.: «Мнемозина», 2010 г.

2. Карточки для групп учащихся с фигурами для вычисления площади сложной фигуры.

3. Чертёжные инструменты.

План урока:

1. Организационный момент.

2. Актуализация знаний.

а) Теоретические вопросы (тест).

б) Постановка проблемы.

3. Изученного нового материала.
          а) поиск решения проблемы;
          б) решение поставленной проблемы.
        4. Закрепление материала.

 а) коллективное решение задач;

Физкультминутка.

       б) самостоятельная работа.

5. Домашнее задание.

6. Итог урока. Рефлексия.

Ход урока.

1. Организационный момент.

Урок мы начнём вот с таких напутствующих слов:

Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно,
И успех тебя ждёт обязательно!

2.Актуализация знаний.

а) Фронтальная работа с сигнальными карточками (у каждого ученика карточки с числами 1, 2, 3, 4; при ответе на вопрос теста ученик поднимает карточку с номером правильного ответа).

1.Квадратный сантиметр – это:

1) площадь квадрата со стороной 1 см;

2) квадрат со стороной 1 см;

3) квадрат с периметром 1 см.

2.Площадь фигуры, изображённой на рисунке, равна:

1 дм

1 дм

1) 8 дм;

2) 8 дм²;

3) 15 дм².

3.Справедливо ли утверждение, что равные фигуры имеют равные периметры и равные площади?

1) да; 2) нет.

4.Площадь прямоугольника определяется по формуле:

1) S = a²;

2) S = 2 • (a + b);

3) S = a • b.

5.Площадь фигуры изображённой на рисунке, равна:

1) 12 см;

2) 8 см; 6 см

3) 16 см.

2 см

б) (Постановка проблемы). 8 м

7 м

2 м

4 м

3 м

Задача. Сколько надо краски, чтобы покрасить пол, который имеет следующую форму (см. рис.), если на 1 м² расходуется 200 г краски?

3.Изучение нового материала.

Что же мы должны узнать, чтобы решить последнюю задачу? (Найти площадь пола, который имеет вид «сложной фигуры».)

Учащиеся формулируют тему и цели урока (если необходимо учитель помогает).

Рассмотрим прямоугольник ABCD.B

N

C

A

K

D

P

M

1 см

Проведём в нем линию KPMN, разбив прямоугольник ABCD на две части: ABNMPK и KPMNCD.

Чему равна площадь ABCD? (15 см²)

Чему равна площадь фигуры ABMNPK? (7 см²)

Чему равна площадь фигуры KPMNCD? (8 см²)

Проанализируйте полученные результаты. (15= = 7 + 8)

Вывод? (Площадь всей фигуры равна сумме площадей её частей.)

S = S₁ + S₂

Как можно применить это свойство для решения нашей задачи?(Разобьём сложную фигуру на части, найдём площади частей, затем площадь всей фигуры.)

8 м

2 м

4 м

3 м

S₂

S₁

S₃

7 м

S₂ = (7 – 4) • (8 – 2 – 3) = 3 • 3 = 9 (м²)

S₃ = 7 • 3 = 21 (м²)

S = S₁ + S₂ + S₃ = 14 + 9 + 21 = 44 (м²)

Давайте составим план решения задач на нахождение площади «сложной фигуры»:

1) Разбиваем фигуру на простые фигуры.

2) Находим площади простых фигур.

3) Находим площадь всей фигуры: S = S₁ + S₂+ …

4.Закрепление материала.

а) Задача 1. (коллективное решение на доске и в тетрадях.) Сколько потребуется плитки, чтобы выложить площадку следующих размеров:

Решение:

30 дм

50 дм

20 дм

60 дм

K

M

D

C

B

A

S₁

S₂

S = S₁ + S₂

S₁ = (60 – 30) • 20 = 600 (дм²)

S₂ = 30 • 50 = 1500 (дм²)

S = 600 + 1500 = 2100 (дм²)

Есть ли другой способ решения? (Рассматриваем предложенные варианты.)

Ответ: 2100 дм².

Задача 2. (коллективное решение на доске и в тетрадях.) Сколько требуется м² линолеума для ремонта комнаты, имеющей следующую форму:

Решение:

3 м

5 м

2 м

S₂

О

М

Р

К

S₁

S = S₁ + S₂

S₁ = 3 • 2 = 6 (м²)

S₂ = ((5 – 3) • 2) : 2 = 2 (м²)

S = 6 + 2 = 8 (м²)

Ответ: 8 м².

Физкультминутка.

А теперь, ребята, встали.

Быстро руки вверх подняли.

В стороны, вперед, назад.

Повернулись вправо, влево.

Тихо сели, вновь за дело.

б) Самостоятельная работа (обучающего характера).

Учащиеся разбиваются на группы (№ 5 – 8 более сильные). Каждая группа - ремонтная бригада.

Задание бригадам: определите, сколько надо краски, чтобы покрасить пол, имеющий форму фигуры, изображённой на карточке, если на 1 м² требуется 200 г краски.

Вы эту фигуру строите своей тетради и записывая все данные, приступаете к выполнению задания. Можете обсуждать решение (но только в своей группе!). Если какая-то группа справляется с заданием быстро, то ей - дополнительное задание (после проверки самостоятельной работы).

Задания для групп:

№ 1

№ 2

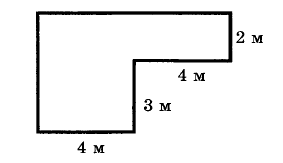
№ 3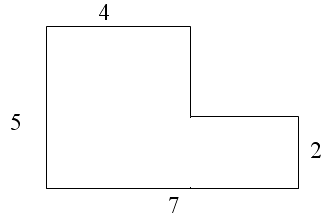

№ 4

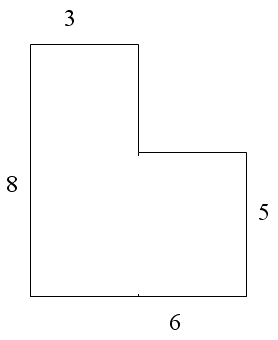
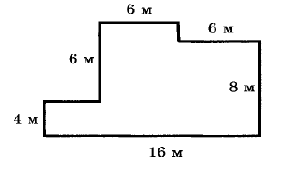
№ 5 № 6

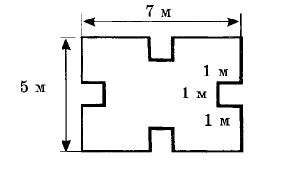
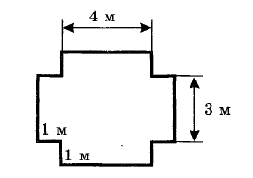
№ 7 № 8

5.Домашнее задание: п. 18, № 718, № 749.

130 м

560 м

410 м

160 м

220 м

Дополнительное задание. План - схема Летнего сада (Санкт-Петербург). Вычислить его площадь.

6.Итоги урока.

Рефлексия. Продолжи фразу:

Сегодня я узнал…

Было интересно…

Было трудно…

Теперь я могу…

Урок дал мне для жизни…