Конспект урока «Теорема Пифагора» по геометрии для 8 класса
Конспект урока для 8 класса «Теорема Пифагора»
Класс:8
Цели урока:
-
Организовать деятельность учащихся по применению теоретических знаний к решению задач. Обеспечить на уроке условия для продуктивной, познавательной деятельности при решении задач конструктивного и творческого уровней
-
Создать условия для развития у учащихся интереса к предмету геометрии и её истории. Содействовать быстрой актуализации и практическому применению полученных знаний, умений и способов действий в нестандартной ситуации.
-
Содействовать формированию у учащихся ответственности за свою деятельность. Способствовать формированию у учащихся ответственности за сохранение и укрепление своего здоровья.
Формирование универсальных учебных действий.
-
Регулятивные УУД:
-
формулировать тему и цель урока с помощью учителя;
-
учить высказывать своё предположение на основе материала учебника.
-
Познавательные УУД:
-
на примерах решения задач составить опору-схему для использования теоремы Пифагора;
-
продолжить формирование умения пользоваться чертежами для решения геометрических задач.
-
Коммуникативные УУД:
-
формировать умение делать выводы из прочитанного в книги, для доказательства теоремы;
-
формировать умение слушать товарищей и высказывать своё мнение.
-
Личностные УУД
-
создание условий к саморазвитию и самообразованию;
-
формирование положительной учебной мотивации, понимание смысла учебной деятельности.
Тип урока: усвоение новых знаний.
Оборудование:учебник геометрии, чертёжные инструменты, готовые чертежи для решения задач.
Ход урока
| Деятельность учителя | Деятельность учащихся | |
| Организационный | Приветствие учащихся. | |
| Постановка целей и задач урока. Мотивация учебной деятельности учащихся | Сегодня на уроке мы научимся находить длины сторон прямоугольного треугольника. Узнаем формулу нахождения гипотенузы прямоугольного треугольника. Выведем формулы для нахождения длины катета, зная длину другого катета и гипотенузу. | |
| Актуализация знаний |
(Фронтальная работа с классом с целью подготовки учащихся к восприятию нового материала)
| Катеты и гипотенуза Катет, лежащий против угла в 30◦ равен половине гипотенузы. |
| Первичное усвоение новых знаний |
Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость, которой была доказана древнегреческим философом и математиком Пифагором (VI в. до н. э.). Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно за долго до Пифагора.
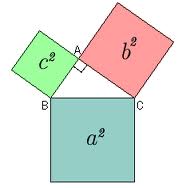
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство теоремы идёт под руководством учителя. На доске и в тетрадях учащихся – рисунок (рис.377) и доказательство. Дано: ∆АВС, АС =b Доказать: c2 = a2+b2 Доказательство:
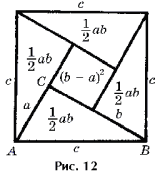
со стороной (a + b) SCKPD = (a + b)² = a² + 2ab + b²
по двум катетам. SBCA = SADM = SEPM = SEKB = ab/2
+ SEKB = c² + 4·(ab/2) = a² + 2ab + b² = c² + 2ab = a² + 2ab + b² , откуда c² = a² + b²
Доказательство Пифагора: Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Доказательство Гофмана:
Построим BF=CB, BF^CB Построим BE=AB, BE^AB Построим AD=AC, AD^AC Точки F, C, D принадлежат одной прямой.
равновелики. Треугольники ABF и ЕCB равны. Значит треугольники ADF и ACE тоже равны.
четырёхугольников общий для них треугольник ABC, получим: 1/2а2+1/2b 2=1/2с 2
а2+ b 2 =с 2 Алгебраическое доказательство индийского математика Бхаскари
| |
| Первичная проверка понимания |
треугольника, если катеты равны 6 и 8 см соответственно.
треугольника, если гипотенуза и катет равны 12 и 13 см соответственно.
AD, если АВ = 5, АС = 13.
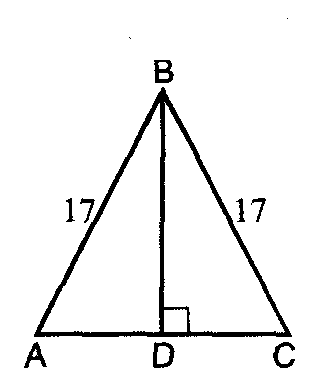
Дано: ∆АВС равнобедренный треугольник, АС – основание, АВ = 17 см, АС = 16 см. Найти: высоту, проведённую к основанию. Решение:
высота, проведённая к основанию, является медианой, поэтому AD = AC :2 = 16 : 2 = 8(см).
Пифагора: AB² = AD² + DB² , откуда DB² = AB² - AD² или ВD² = 17² - 8² = 225. Т.к. DB > 0, то DB = 15 см. | |
| Первичное закрепление | Занимательные задачи по теме: «Теорема Пифагора».
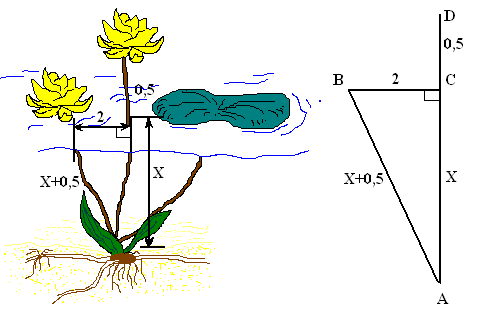
Над озером тихим С полфута размером Высился лотоса цвет. Он рос одиноко, И ветер порывом Отнёс его в сторону. Нет Боле цветка над водой. Нашёл же рыбак его Ранней весною В двух футах от места, где рос. Итак, предложу я вопрос: “Как озера вода здесь глубока?” Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ?
Решение: Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 . Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2, (Х + 0,5)2 – Х2 = 22 , Х2 + Х + 0,25 – Х2 = 4, Х = 3,75. Таким образом, глубина озера составляет 3,75 фута. 3, 75 • 0,3 = 1,125 (м) Ответ: 3,75 фута или 1, 125 м.
XIIв. Бхаскары На берегу реки рос тополь одинокий.
Решение. Пусть CD – высота ствола. BD = АВ По теореме Пифагора имеем АВ = 5 . CD = CB + BD, CD = 3 + 5 =8. Ответ: 8 футов. | |
| Информация о домашнем задании, инструктаж по его выполнению |
доказательства теоремы. Найдите другие способы доказательства этой теоремы.
Пифагора называют теоремой пчёлки или теоремой невесты?» | |
| Рефлексия | О теореме Пифагора Пребудет вечной истина, как скоро A.Шамиссо Чем необычный был для вас сегодняшний урок? - Что нового и интересного вы узнали на уроке? - Что научились делать? - Оцените удовлетворенность своей работой на уроке с помощью карточек. - Спасибо за урок. До свидания. |
Здесь представлен конспект к уроку на тему «Теорема Пифагора», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

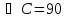 ◦, АВ = с, ВС =
◦, АВ = с, ВС =