Конспект урока «Решение задач с помощью теоремы Пифагора» по геометрии для 8 класса

Использование кейс - технологий на уроках математики.

Урок геометрии в 8 классе.

Тема урока: Решение задач с помощью теоремы Пифагора.

Цели педагогической деятельности:

1. Закрепить знание теоремы Пифагора и теоремы, обратной теореме Пифагора.

2. Развивать умения:

• уметь применять теорему Пифагора на практике;

• принимать самостоятельные решения и выдвигать собственные идеи.

3. Воспитывать:

• умение работать в коллективе;

• способность брать на себя ответственность.

Основные понятия:

• теорема Пифагора;

• теорема, обратная теореме Пифагора;

• виды треугольников.

Раздаточный материал:

• кейс с вопросами - 25 штук;

• набор карточек с тремя уровнями сложности - 5 комплектов;

• жетоны для распределения по группам;

• жетоны для выдачи группам за решённые задачи;

• критерии выставления оценок за аукцион. (Приложение № 1)

Основные этапы урока.

1. Организационная деятельность. Слово учителя. Знакомство с ходом урока.

2. Актуализация знаний учащихся.

3. Устный счёт.

4. Самостоятельная работа учащихся в виде аукциона. Итоги аукциона.

5. Работа с кейсом. Анализ.

6. Домашнее задание.

7. Итог урока.

Ход урока.

1. Организационные моменты.

При входе в кабинет учащиеся берут жетоны и рассаживаются по группам за столы, на которых лежит выбранный ими жетон. Учитель знакомит с ходом работы на уроке.

2. Актуализация знаний учащихся.

• Сформулировать теорему Пифагора.

• Сформулировать теорему, обратную теореме Пифагора.

• Сформулировать теорему о средней линии треугольника.

• Перечислить свойства прямоугольного треугольника.

3. Устный счёт по готовым чертежам. (Приложение № 2)

4. Аукцион «Решение разноуровневых задач в группах». (Приложение № 3)

Учитель знакомит ребят с правилами аукциона. Группы определяют своего лидера,

который возьмёт на себя руководство группой. Вручение жетонов учителем за верно решённую задачу. Подведение итогов аукциона.

5. Работа с кейсом.

• Вступительное слово учителя. Мы с вами рассматривали много примеров применения теоремы Пифагора в жизни. Сейчас познакомимся ещё с одним. Учитель знакомит ребят с кейсом. (Приложение № 4)

• Работа с кейсом.

• Анализ ситуации с использованием метода «Мозговая атака на доске».

6. Домашнее задание.

- Сочинить сказку или рассказ на применение теоремы Пифагора (мёртвый кейс).

Приложение №1.

Критерии выставлении оценок.

2-3 балла- «3»; 4 — 5 баллов - «4»; От 6 баллов - «5».

Приложение № 2.

Задачи для устного счета.

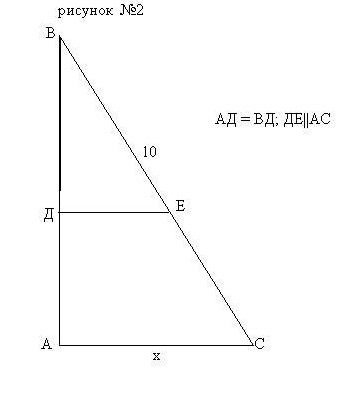
Задание: найдите х.

1)

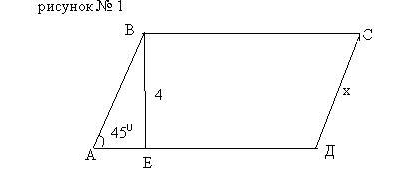
2)

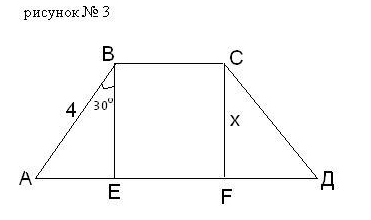
3)

Приложение № 3.

Задачи для аукциона.

(1 балл) Стороны прямоугольника равны 9 см и 12 см. Найдите диагонали

прямоугольника.

(1 балл) Периметр равностороннего треугольника равен 6 см. Найдите его высоту.

(1 балл) Катеты прямоугольного треугольника равны 5 см и 12 см. Найдите

периметр треугольника.

(3 балла) Основания прямоугольной трапеции равны 2 см и 10 см, а боковые

стороны относятся как 3:5. Найдите периметр трапеции.

(3 балла) Периметр равнобедренного треугольника равен 16 см, а его основание

равно 6 см. Найдите биссектрису треугольника, проведённую к основанию.

(3 балла) Основания прямоугольной трапеции равны 15 см и 6 см, а меньшая

диагональ является биссектрисой тупого угла. Найдите периметр трапеции.

(5 баллов) Диагонали ромба относятся как 3:4, а сторона равна 50 см. Найдите

диагонали и высоту ромба.

(5 баллов) Боковая сторона равнобедренного треугольника равна 17 см, а высота

проведённая к ней, равна 8 см. Найдите основание треугольника.

(5 баллов) Диагонали параллелограмма равны 30 см и 26 см, а высота равна 24 см.

Найдите стороны параллелограмма.

Приложение № 4.

Кейс «Помогла теорема Пифагора».

Действующие лица: - подозреваемый

• следователь

• потерпевший.

Цели:

• закрепить изучаемый материал.

• показать применение теоремы Пифагора в жизненной ситуации.

Проблемная ситуация: доказать с помощью теоремы Пифагора невиновность или виновность подозреваемого.

Этот эпизод взят из реальной следственной практики. Получив сообщение о краже, следователь выехал на место происшествия. Заявитель утверждал, что преступник проник в помещение, где хранились ценности, через окно. Осмотр показал, что подоконник находится на расстоянии 150 см от земли. Поверхность земли на расстоянии 200 см. от стены здания покрыта густой порослью, не имевшей никаких следов повреждений. При осмотре не было найдено никаких технических средств типа лестницы. Возникло предположение, что преступник проникал в помещение через окно каким-то образом преодолев расстояние между наружным краем поросли и подоконником. Оно было определено с помощью теоремы Пифагора. Следователь выдвинул версию об инсценировке кражи.

1. Проанализируйте ситуацию.

2. Выявите моменты, указывающие на возможность применения теоремы Пифагора.

3. На основании каких фактов следователь выдвинул версию о невиновности подозреваемого? Аргументируйте свой ответ.

4. Какие бы вы сделали выводы на месте следователя?