Конспект урока «Решение задач по теме «Четырехугольники» по геометрии для 8 класса

Урок геометрии в 8 классе по теме

«Решение задач по теме «Четырехугольники»»

Тимофеева Галина Александровна, учитель математики

МБОУ «Средняя школа № 12», г.Щекино, Тульская область

Цели: систематизировать основные свойства и признаки четырехугольников, их определения, установить связь между основными фигурами, изучаемыми в данной теме, активизировать работу учащихся, решение задач.

Оборудование: мультимедийный проектор, плакат «Геометрические фигуры», раздаточный материал (наборы геометрических фигур).

Ход урока

Дети! Сегодня у нас урок решения задач по теме «Четырехугольники». На этом уроке мы повторим и систематизируем основные свойства и признаки четырехугольников, их определения; установим связь между основными фигурами, изучаемыми в данной теме, будем решать задачи.

А пройдет наш урок в виде заседания клуба юных математиков и работать будем по следующему плану:

План

1. Защита геометрических фигур

2. Спеши видеть

3. Практическая работа

4. Решение задач

5. Тестирование

6. Итоги

I этап нашего заседания «Защита геометрических фигур»

Каждая группа будет защищать свою фигуру….

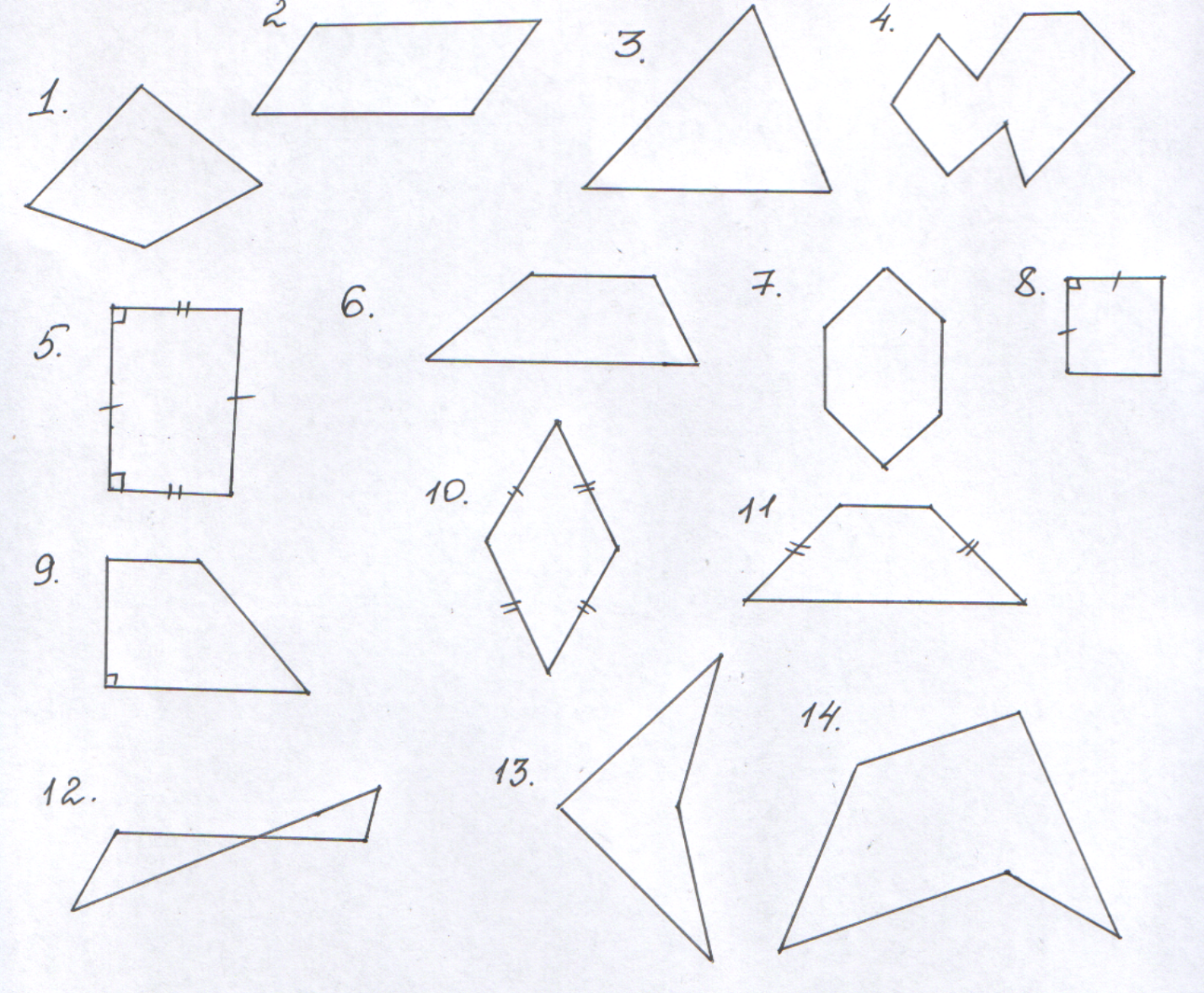
Внимательно посмотрите на плакат «Геометрические фигуры». Найдите на нем свою фигуру и дайте ей характеристику.

1 стол. Наша фигура – параллелограмм. На плакате под № 2.

Слово параллелограмм греческого происхождения и было введено Евклидом. Понятие параллелограмма и некоторые его свойства были известны ученикам Пифагора.

Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма :

1. В параллелограмме противоположные стороны и углы равны.

2. Диагонали параллелограмма точкой пересечения делятся пополам.

Признаки

1. Если в четырехугольнике две стороны равны и параллельны, то это параллелограмм.

2. Если в четырехугольнике противоположные стороны попарно равны, то это параллелограмм.

3. Если в четырехугольнике диагонали пересекаются точкой пересечения пополам, то это параллелограмм.

2 стол. Наша фигура – трапеция.

Трапеция – четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Трапеция – греческое слово, означавшее в древности «столик»(по-гречески «трапедзион» означает обеденный стол). Для сравнения современные слова трапеза, трапезная.

Трапеция бывает произвольная (как на плакате под № 6), прямоугольной (как на плакате под № 9) и равнобедренной (как на плакате под № 11).

Признак

Если в четырехугольнике две стороны параллельны, то это трапеция.

Свойства

1. В равнобедренной трапеции углы при основаниях равны

2. В равнобедренной трапеции диагонали равны

3. В прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям

3 стол. Наша фигура – прямоугольник. № 5

Прямоугольник – это параллелограмм, у которого все углы прямые.

Прямоугольник обладает всеми свойствами параллелограмма. У прямоугольника есть и свое свойство.

В прямоугольнике диагонали равны.

Признак

Если в параллелограмме диагонали равны, то это прямоугольник.

4 стол. Наша фигура – ромб № 10.

Ромб – параллелограмм, у которого все стороны равны.

Ромб так же как и прямоугольник обладает всеми свойствами параллелограмма, но у него есть свое особое свойство.

Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.

Слово «ромб» греческого происхождения, оно в древности означало вращающееся тело, веретено, юлу. Ромб так же имел смысл бубна, который в древности был не круглым, а четырехугольным.

Признак

Если в параллелограмме диагонали взаимно перпендикулярны и делят его углы пополам, то это ромб.

5 стол. Наша фигура – квадрат. На плакате под №8.

Квадрат – прямоугольник, у которого все стороны равны.

Квадрат обладает свойствами ромба и прямоугольника, т.е.:

1. Все углы квадрата прямые

2. Диагонали равны

3. Диагонали взаимно перпендикулярны

4. Диагонали точкой пересечения делятся пополам

5. Диагонали делят углы квадрата пополам

Термин «квадрат» происходит от латинского «квадратум».

Признаки

1. Если в ромбе диагонали равны, то это квадрат.

2. Если в прямоугольнике диагонали взаимно перпендикулярны, то это квадрат.

Итак, мы повторили определения, свойства и признаки фигур.

В геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.

Кто ничего не замечает, тот ничего не изучает.

Кто ничего не изучает, тот вечно хнычет и скучает.

II этап нашего заседания - «Спешите видеть».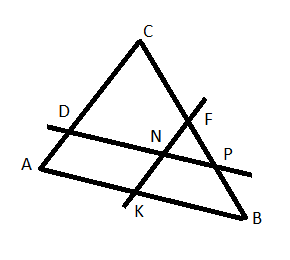

ΔАВС, DP//AB, KF //AC. На какие фигуры разбит ΔАВС прямыми DP и KF?

Δ KFB, ΔNFP, ΔDPC

Параллелограмм ADNK

Трапеции ADPB, KNPB, ACFK, DCFN

МОЛОДЦЫ!! Умеете видеть и выделять нужные фигуры.

Переходим к следующему этапу заседания. У нас «Практическая работа» - III этап.

У вас на партах лежат конверты с набором геометрических фигур. Ваша задача составить из них вашу фигуру, а потом, выполнить необходимые измерения и найти ее периметр.

Как только выполните задание – поднимите руку (листы с выполненным заданием приклеить к доске снизу на скотч).

IV этап заседания клуба «Решение задач»

Из задач, которые вы видите на экране, выберите ту, которая относится к вашей фигуре. Решение запишите в тетради.

№ 1. Периметр прямоугольника равен 48 см. Найдите его стороны, если они относятся, как 1:2. (ответ: 8 см и 16 см)

№ 2. Диагонали ромба KMNPпересекаются в точке О. найдите углы ΔКОМ, если 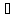MNP= 80°. (ответ: 40°, 50°, 90°)

№ 3. В равнобокой трапеции один угол равен 70 °. Найдите остальные углы трапеции. (ответ: 70° и 110°)

№ 4. Периметр параллелограмма равен 88 см. Найдите стороны параллелограмма, если одна из них в 3 раза больше другой. (ответ: 11см и 33 см)

№ 5. CDMN- квадрат, диагонали которого пересекаются в точке О. Чему равны углы Δ CON? (ответ: 45°, 45°, 90°)

Следующую задачу из вашего учебника № 401а выполним вместе.

Прочитайте условие.

• Какая фигура дана?

• Что о ней известно?

• Что нужно найти?

• Что для этого нужно знать?

К доске решать эту задачу пойдет …

У всех получился такой же ответ? Покажите на доске свое решение.

Ответ: 198,1 см или 122,6 см.

Вы хорошо справились с решением поставленных задач.

V этап – Тестирование.

На каждом столе лежат тесты разного уровня сложности: на «3», на «4» и на «5». Выберите для себя тест, подходящей сложности и решите его.

Самопроверка (на экран выводятся с помощью мультимедийного проектора правильные ответы).

VI этап – поведение итогов. Вы уже обратили внимание на плакат «Генеалогическое древо четырехугольников».

Словарь Ожигова

Словарь Даля
Генеалогия – это раздел истории, изучающий происхождение и связи отдельных родов.	Генеалогическое древо – это изображение истории рода в виде разветвленного дерева

Для нас генеалогическое древо четырехугольников – это изображение различных видов четырехугольников в форме дерева. Посмотрите на него внимательнее.

Итак, в ходе нашего заседания были показаны хорошие знания теоретического материала по теме «Четырехугольники», умение применять эти знания на практике при решении задач, при составлении геометрических фигур, при тестировании. Все группы работали активно и результатом стали следующие оценки: …

Домашнее задание: № 401б, № 425.

Литература.

1.Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия 10 – 11 классы. Издательство « Просвещение» - 2001 г.

2.Атанасян Л.С., Бутузов В.Ф., и др. Геометрия 7 -9 классы: учеб. для общеобразоват. учреждений. Издательство – М: Просвещение, 2009.

3.Гусев В.А., Мордкович А.Т. Математический справочный материал. Издательство « Просвещение» - 1986 г.

4.Смирнов В.А., Смирнова И.М. Геометрия. Издательство « Просвещение» - 2001 г.

5.Роганин А.Н., Немченко К.Э., Лысикова И.В. и др. Современный справочник школьника: 5-11 классы – М.Эксмо, 2011 г.

6.Мельникова Н.Б., Лепихова Н.М., Лудина Г.Б., Захарова Г.А.Задачник- практикум.Геометрия ( к уч. Л.С.Атанасяна и др.) 7 кл. Издательство Интелект Центр,2007 г.

7.Ященко И.В., Шестаков С.А., Захаров П.И.Математика. Рабочая тетрадь для подготовки к экзамену. Издательство МЦНМО. Изд. « Экзамен», 2010 г.

Приложение 1.

Плакат «Геометрические фигуры»

Приложение 2.

Тест по теме « Четырехугольники».

На «3».

1.Параллелограмм – это четырехугольник , у которого …

а)… противоположные стороны равны;

б)… противоположные углы равны;

в)… противоположные стороны параллельны.

2. Что означает следующая формула Р = 2( a + b)

а) периметр трапеции равен удвоенной сумме сторон,

б) периметр ромба равен сумме сторон,

в) периметр прямоугольника равен удвоенной сумме соседних сторон.

3.Ромб – это параллелограмм, у которого …

а) … противоположные углы равны,

б) … диагонали являются биссектрисами его углов,

в) … все стороны равны.

На «4».

1. Сумма градусных мер трех углов параллелограмма равна 300°.найди величину тупого угла этого параллелограмма.

1. 100°

2. 120°

3. 150°

4. 140°

2. Если сторона ромба равна одной из его диагоналей, то величина большего угла этого ромба равна

1. 150°

2. 140°

3. 130°

4. 120°

3. В прямоугольной трапеции острый угол равен 45°. Меньшая боковая сторона и меньшее основание равны по 10 см. Найди большее основание.

1. 25 см

2. 20см

3. 30см

4. 45 см

На «5».

1. Периметр параллелограмма равен 20 см. Какое наибольшее целое значение может принимать длина одной из сторон этого параллелограмма?

1. 19 см

2. 9 см

3. 11 см

4. 8 см

2. Найти острый угол между диагоналями прямоугольника, если одна из них делит угол при вершине прямоугольника в отношении 2 : 7.

1. 10°

2. 40°

3. 30°

4. 20°

3. В прямоугольной трапеции острый угол равен 60°. Большая боковая сторона и большее основание равны по 20 см. Найди меньшее основание.

1. 20см

2. 40см

3. 30см

4. 50см

Вариант 1

1. Параллелограмм – это …

а) … четырехугольник , у которого противоположные стороны равны;

б) … четырехугольник , у которого противоположные углы равны;

в) … четырехугольник , у которого противоположные стороны параллельны.

2. Что означает следующая формула Р = 2( a + b)

а) периметр трапеции равен удвоенной сумме сторон,

б) периметр ромба равен сумме сторон,

в) периметр прямоугольника равен удвоенной сумме соседних сторон.

3. Диагонали ромба

1. взаимно перпендикулярны,

2. равны,

3. пересекаются и точкой пересечения делятся в отношении 2:1.

4. Трапеция называется прямоугольной, если

1. у нее три прямых угла,

2. у нее два прямых угла,

3. у нее два противоположных угла прямые

5. Периметр квадрата вычисляется по формуле

1. 3

2. Р = 2( a + b)

3. Р = 4( a + b)

Вариант 2

1. Ромб – это …

а) … параллелограмм, у которого противоположные углы равны,

б) … параллелограмм, у которого диагонали являются биссектрисами его углов,

в) … параллелограмм, у которого все стороны равны.

2. Трапеция называется равнобедренной, если

1. у нее равны боковые стороны,

2. у нее две стороны равны,

3. у нее все стороны равны.

3. У квадрата

1. прямая, содержащая диагональ, является его осью симметрии,

2. периметр вычисляется по формуле S= 4 a,

3. сумма углов равна 180°.

4. В прямоугольнике

1. диагонали перпендикулярны,

2. диагонали являются биссектрисами углов,

3. диагонали точкой пересечения делятся пополам.

5. Признак параллелограмма

1. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм,

2. Если в четырехугольнике противоположные стороны попарно параллельны, то этот четырехугольник – параллелограмм,

3. Если середина диагонали четырехугольника является центром симметрии, то это - параллелограмм.

Вариант 3

1. Прямоугольник – это …

1. … параллелограмм, у которого все углы прямые,

2. … параллелограмм, у которого диагонали равны,

3. … параллелограмм, у которого

2. В равнобедренной трапеции

1. противолежащие углы равны,

2. углы при основании равны,

3. диагонали делят углы пополам.

3. В ромбе

1. Точка пересечения диагоналей является его центром симметрии,

2. прямая, содержащая сторону является его осью симметрии,

3. диагонали равны.

4. В квадрате

1. диагональ делит его на два равнобедренных треугольника

2. сумма всех углов равна 270°

3. сумма противоположных углов равна 120°

5. Свойство параллелограмма:

1. Каждая диагональ параллелограмма делит его на два равных треугольника

2. Диагонали параллелограмма взаимно перпендикулярны

3. Диагонали параллелограмма являются биссектрисами его внутренних углов

Вариант 4

1. Квадрат – это …

1. …параллелограмм, у которого все стороны равны,

2. … прямоугольник, у которого все стороны равны,

3. … ромб, у которого равны диагонали.

2. Признак параллелограмма

1. Если в четырехугольнике две противоположные стороны равны и параллельны , то этот четырехугольник – параллелограмм

2. Если в четырехугольнике середина диагонали является его центром симметрии, то этот четырехугольник – параллелограмм

3. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм

3. В прямоугольной трапеции

1. сумма противоположных углов равна 180°

2. боковые стороны равны

3. два прямых угла.

4. Свойство ромба:

1. все углы равны

2. диагонали взаимно перпендикулярны

3. диагонали равны

5. У прямоугольника

1. сумма всех углов равна 360°

2. все стороны равны

3. периметр равен сумме двух его сторон.

Вариант 5

1. Трапеция - это …

1. …четырехугольник, у которого только две противолежащие стороны параллельны,

2. … параллелограмм, у которого две стороны не параллельны,

3. …произвольный четырехугольник.

2. Квадрат имеет

1. две оси симметрии

2. четыре оси симметрии,

3. пять осей симметрии.

3. У параллелограмма

1. один центр симметрии

2. три диагонали

3. сумма противоположных углов равна 180°.

4. Периметр ромба вычисляется по формуле

1. Р = 4 a,

2. S = 2 a

3. Р = 4( a + b)

6. Свойства прямоугольника

1. Диагонали прямоугольника равны

2. Диагонали прямоугольника взаимно перпендикулярны

3. Диагонали прямоугольника являются биссектрисами его внутренних углов