Конспект урока «Равнобедренный треугольник и его свойства» по геометрии
Тема урока: « Равнобедренный треугольник и его свойства»
Цель урока: изучить и доказать свойства равнобедренного треугольника.
Задачи урока:
образовательные:
-
повторить основные понятия по теме «Треугольник», определение равнобедренного и равностороннего треугольника;
-
выполнить лабораторную работу «Градусная мера углов равнобедренного треугольника при основании», сделать вывод;
-
доказать свойства равнобедренного треугольника;
-
формировать умение применять эти свойства,
развивающие:
-
развивать логическое и пространственное мышление, творческую и мыслительную деятельность учащихся, способность к «видению» проблемы;
-
формировать способности к оценке собственной деятельности,
воспитательные:
-
формировать осознанное и ответственное отношение к своей деятельности;
-
формировать информационную и коммуникативную компетенции.
Место урока в учебном плане: на изучение темы в курсе геометрии 8 класса отводится два урока, данный урок является первым.
Тип урока: урок изучения нового материала.
Оборудование и материалы урока:
компьютер, интерактивная доска, проектор, передвижной компьютерный класс (компьютер на каждом ученическом столе), презентация;
раздаточный материал: тест, текст лабораторной работы № 3 и интерактивная модель, установленная на компьютерах, текст самостоятельной работы, схема
«Паспорта равнобедренного треугольника».
План урока.
-
Организационный момент.
-
Актуализация опорных знаний. Тест по готовым рисункам.
-
Постановка учебной задачи.
-
«Открытие» учащимися нового знания.
-
Первичное закрепление: лабораторная работа, доказательство свойств.
-
Включение в систему знаний «новых» знаний.
-
Самостоятельная работа с самопроверкой.
-
Подведение итогов урока. Рефлексия.
-
Задание на дом.
Ход урока
-
Организационный момент – 2 минуты.
Цель: формирование мотивации.
Учитель: Сегодня мы продолжим знакомство с самой популярной в школьном курсе геометрической фигурой. Это самая простая замкнутая прямолинейная фигура, свойства которой человек узнал еще в глубокой древности, так как она имела широкое применение в практической жизни. Вы догадались, что это за фигура? – Треугольник.
-
Актуализация опорных знаний. Тест по готовым рисункам, проверка ответов: 1 этап – в паре, 2 этап – фронтально – 4 минуты.
Цель: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося.
Учитель: Как вы думаете, на какие вопросы вы должны знать ответ, изучив темы «Первый признак равенства треугольников», «Медианы, биссектрисы и высоты треугольника»? (Слайд 2)
Учащиеся задают вопросы и отвечают на них:
-
Что называется треугольником?
-
Элементы треугольника? Периметр треугольника?
-
Первый признак равенства треугольников?
-
Какие отрезки называются медианой, биссектрисой и высотой треугольника? Сколько высот, медиан, биссектрис в треугольнике?
Повторив теоретический материал, предлагаю вам самостоятельно ответить на вопросы теста, ответы записать в таблицу.
Тест: (Слайд 3,4)
№1. На каком рисунке построена высота?
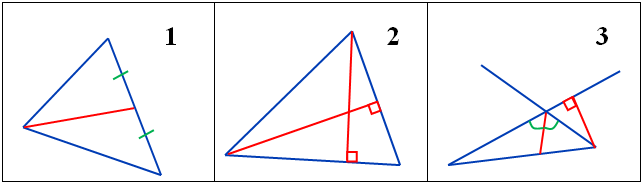
№2. На каком рисунке построена медиана?
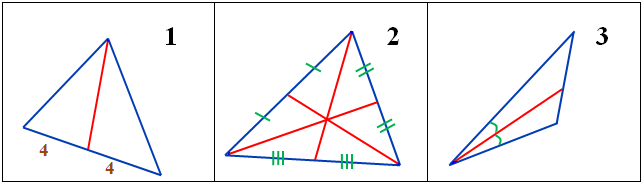
№3. На каком рисунке построена биссектриса?
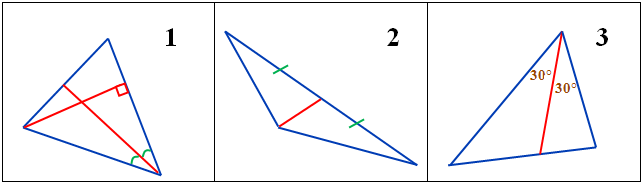
№4. На каком рисунке есть равные треугольники?
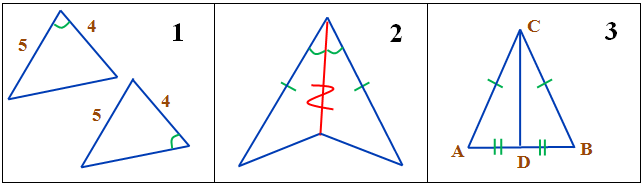
-
Постановка учебной задачи – 3 минуты.
Цель: обсуждение затруднений («Почему возникли затруднения?», «Чего мы еще не знаем?»).
Проверка ответов теста (Слайд 5): после проверки в паре, учитель предлагает сильному ученику продиктовать ответы. Затруднение вызывает ответ к последней задаче.
| №1 | №2 | №3 | №4 | |
| Ответ | 2, 3 | 1, 2 | 1, 3 | 2, 3? |
Учитель: Почему нельзя ответить на вопрос в последней задаче? – Мы не знаем, равны ли углы А и В?
-
«Открытие» учащимися нового знания – 3 минуты.
Цель: устранение возникшего затруднения решения задачи и обсуждение проекта ее решения, формулировка темы и цели урока.
После обсуждения, учащиеся выдвигают гипотезу: если сможем установить равенство углов А и В, то ответ в задании №4 - 2, 3.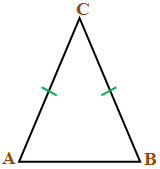
Учитель предлагает проанализировать рисунок. В ходе беседы учащиеся определяют вид треугольника АВС (Слайд 6), повторяют определение равнобедренного треугольника, его элементы: боковые стороны, основание, углы при основании и угол, противолежащий основанию.
Опираясь на выдвинутую гипотезу и предыдущие рассуждения, учащиеся формулируют тему урока и его цель (Слайд 7).
Учитель: Чтобы решить последнюю задачу теста, необходимо…? - установить равенство углов А и В.
Учитель: Какие углы называются равными и что для этого надо сделать? - Углы с равными градусными мерами. Измерить с помощью транспортира их градусную меру.
-
Первичное закрепление учащимися нового знания – 15 минут.
Цель: вывод свойства углов при основании равнобедренного треугольника в ходе выполнения лабораторной работы.
-
Лабораторная работа (Слайд 8) – 9 минут.
Цель: сравнить градусные меры углов равнобедренного треугольника при основании.
Перед выполнением лабораторной работы, учащиеся повторяют построение равнобедренного треугольника с помощью линейки и карандаша: построить точку, отложить от нее два равных отрезка и соединить их концы.
-
Доказательство свойств – 6 минут.
Цель: доказать свойства равнобедренного треугольника, опираясь на первый признак равенства треугольников.
Учитель: Достаточно ли сформулировав свойство, использовать его при решении задач? – Нет. Надо доказать его.
Доказательство записывается на доске, опираясь на рисунок (Слайд 9):
1. Проводим биссектрису СD.
2. Рассмотрим Δ АСD и Δ DBC:
АС = СВ , т.к. Δ АВС – равнобедренный;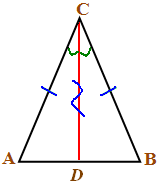
СD – общая сторона;
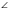 АСD =
АСD = 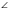 DCB, т.к. АD – биссектриса.
DCB, т.к. АD – биссектриса.
Значит, Δ АСD = Δ DBC.
-
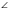 А =
А = 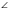 B – углы при основании;
B – углы при основании; -
АD = DB
 CD – медиана;
CD – медиана; -
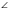 АDС =
АDС =  СDB = 90°
СDB = 90°  CD – высота.
CD – высота.
Учитель: А теперь сформулируйте доказанные нами свойства равнобедренного треугольника. – Углы при основании равны; биссектриса, проведенная к основанию, является медианой и высотой.
Учитель: Можно ли утверждать, что биссектриса, медиана и высота, проведенные к основанию, совпадают? – Да.
Учитель: Какой вывод можно сделать из последнего утверждения? – Высота, проведенная к основанию, будет биссектрисой и медианой, а медиана, проведенная к основанию, будет биссектрисой и высотой.
Учитель: Вернемся к нерешенной задаче теста. – Гипотеза подтвердилась, ответ 2 и 3. (Слайд 10)
-
Включение в систему знаний «новых» знаний – 8 минут.
Цель: научить применять свойства при решении задач.
Решение задач № 1, №2 по готовым рисункам на слайдах 3, 4.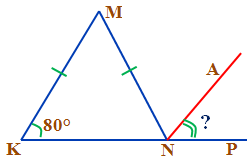
Задача №1. (Слайд 11) На рисунке  МKN = 80°. Найдите
МKN = 80°. Найдите  ANP, если NA- биссектриса
ANP, если NA- биссектриса  MNP.
MNP.
Задача № 2. (Слайд 12) На рисунке  1 =
1 =  2, АС = АD. Найдите МВС и МD, если МС = 3см.
2, АС = АD. Найдите МВС и МD, если МС = 3см. 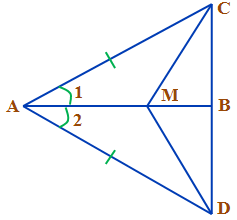
Запись решений на интерактивной доске и в тетрадях.
-
Самостоятельная работа с самопроверкой (Слайд 13) – 5 минут.
-
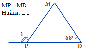
1 Вариант
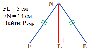
2 Вариант

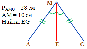
-
Решение и ответы (Слайд 14)
Вариант 1
Вариант2
-
МР = МD, ΔРМD – равнобедренный.
-
 MPD =
MPD = 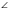 MDP = 68° - углы при основании.
MDP = 68° - углы при основании. -
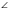 1 = 180° -
1 = 180° - 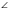 MPD = 180° - 68° = 112°.
MPD = 180° - 68° = 112°.
Ответ: 112°
-
AC = AD, ΔACD – равнобедренный.
-
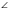 ADC =
ADC = 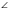 MDD = 40° - вертикальные углы.
MDD = 40° - вертикальные углы. -
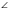 С =
С = 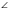 ADC = 40°- углы при основании.
ADC = 40°- углы при основании.
Ответ: 40°
-
FN = NE = 14 см, Δ FNE – равнобедренный.
-
NL – высота и медиана, по свойству равнобедренного треугольника; FL = LE = 5 cм.
-
EF = FL + LE = 5 + 5 = 10 (cм).
-
PFNE = FN+NE+FE,
PFNE =14+14+10=28(см).
Ответ: 28 см.
-
AМ = MG = 10 см, Δ AMG – равнобедренный.
-
AG = PAMG – AM – MG =28- 10-10 = 8 (см).
-
ME – биссектриса и медиана, по свойству равнобедренного треугольника; AE = EG = AG : 2 = 8 : 2 = 4(cм).
Ответ: 4 см.
-
-
Подведение итогов урока – 3 минуты.
Цель: Рефлексия учебной деятельности.
Учитель предлагает учащимся ответить на следующие вопросы:
Что нового узнали на занятии?
Что использовали для «открытия» нового знания?
Достиг ли урок своей цели?
Проанализируйте и оцените свою работу сегодня.
-
Задание на дом – 2 минуты.
Домашнее задание носит дифференцированный характер:
-
составить Паспорт равнобедренного треугольника. Для образца можно использовать схему (Слайд 15):
-
решить задачи (Слайд 16):
-
для всех учащихся: «Геометрия 7-9», Атанасян Л.С. и др., §2 п. 18 №107,118;
-
для более подготовленных учащихся дополнительно № 163.
Здесь представлен конспект к уроку на тему «Равнобедренный треугольник и его свойства», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

