Конспект урока «Теорема Пифагора» по геометрии для 8 класса

Автор: Сокольникова Галина Александровна, МКОУ Невельская ООШ, учитель математики.

Предмет: Геометрия, 8 класс.

1. Название темы: Площадь

2. Роль и место данной темы в курсе: в курсе геометрия изучается тема площадь, между темами многоугольники и подобие треугольников.

3. Перечень вопросов, изучаемых в данной теме: площади многоугольников и треугольников, теорема Пифагора.

4. Тема урока: Теорема Пифагора.

5. Урок изучения нового материала.

6. Основные особенности использования цифровых образовательных Интернет-ресурсов и компьютерных программных средств: образовательные Интернет ресурсы http://ru.wikipedia.org, http://www.etudes.ru/index.php

7. Технические средств: подключение компьютера к сети Интернет

8. Программные средства: Microsoft Office 2007, 2010.

9. Ресурсы Интернет: http://ru.wikipedia.org/wiki/Теорема_Пифагора

10. Использование компьютера при подготовке учителя к уроку: подборка интернет ресурсов.

11. Ожидаемые результаты обучения: учащиеся должны усвоить материал урока и применять знания на практике.

Урок по теме: « Теорема Пифагора»

Цель: Изучить Теорему Пифагора.

Задачи:

• Образовательные: Изучить доказательство теоремы Пифагора, решать задачи на применение данной теоремы.

• Воспитательные: Воспитывать научное мировоззрение.

• Развивающие: Формировать умения применять полученные знания в новых условиях.

Оборудование и ресурсы:

1. http://ru.wikipedia.org/wiki/Теорема_Пифагора

2. http://www.etudes.ru/ru/etudes/pifagor/

Перечень используемых цифровых ресурсов на уроке: википедия, математические этюды.

Отличительные особенности данного урока: учащиеся приобретают знания, расширяют кругозор, используя нетрадиционные источники информации.

Работа учителя на уроке: координатор.

Описание деятельности учащихся: учащиеся выходят на образовательный ресурс http://ru.wikipedia.org/wiki/Теорема_Пифагора, знакомятся с доказательством теоремы, создают документ и вставляют одно из доказательств теоремы с чертежом, распечатывают этот документ и вставляют в тетрадь. Сравнивают теоретический материал с данными в учебнике, отметить интересные факты, используя предложенный алгоритм решают задачи на применение теоремы Пифагора.

Доказательство теоремы Пифагора, которые учащиеся найдут на данной образовательном ресурсе.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

История:

Чу-пей 500—200 лет до нашей эры. Слева надпись: сумма квадратов длин высоты и основания есть квадрат длины гипотенузы.

В древнекитайской книге Чу-пей (англ.) (кит. 周髀算經) говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.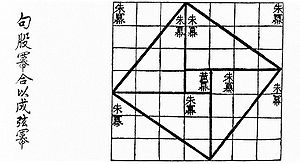

Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I(согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника^[1].

Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.^[7]

Формулировки:

Теорема Пифагора: Сумма площадей квадратов, опирающихся на катеты (a и b), равна площади квадрата, построенного на гипотенузе (c).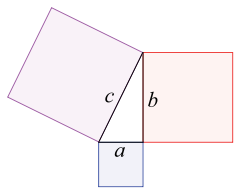

Геометрическая формулировка:

Изначально теорема была сформулирована следующим образом:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Обратная теорема Пифагора:

Для всякой тройки положительных чисел а, в и с, такой, что а2+в2=с2, существует прямоугольный треугольник с катетами а и в и гипотенузой с

Доказательства:

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы^[8]. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

1.Через подобные треугольники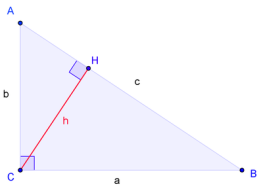

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Что и требовалось доказать

2.Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

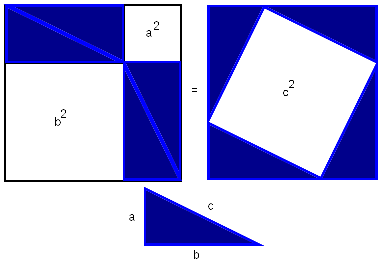
1.Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.

2.Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.

3.Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.

Что и требовалось доказать.

Доказательство Евклида

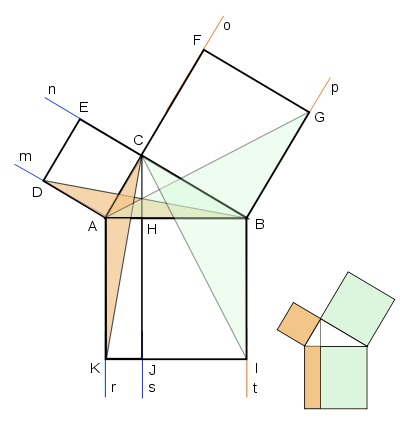
Половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Данное доказательство также получило название «Пифагоровы штаны».

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.

Используя алгоритм решения задач по теореме Пифагора, решите №483, №484, №486.

Алгоритм решения задач по теореме Пифагора

1. Внимательно прочти задачу, разберись с условием.

2. По условию задачи сделай чертёж.

3. Выдели на чертеже прямоугольный треугольник.

4. Найди катеты и гипотенузу.

5. Запиши теорему Пифагора и соотнеси данные в задаче с ней.

6. Выполни подстановку данных.

7. Соотнеси полученный ответ с вопросом задачи и смыслом условия.

Д/З Учащиеся выходят на образовательный ресурс http://www.etudes.ru/ru/etudes/pifagor/ доказать теорему Пифагора четырьмя способами, используя головоломку. Работа с головоломкой осуществляется правой кнопкой мыши.

Межпредметные связи на уроке: информатика (умение работать в сети Интернет, поиск информации на представленных образовательных ресурсах)

Итоги урока: Учащиеся узнали историю доказательства теоремы Пифагора, познакомились с несколькими формулировками этой теоремы, дома пробовали придумывать свои задачи на доказательство теоремы.