Конспект урока «Площади. Теорема Пифагора» по геометрии для 8 класса
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №16»
Урок обобщения в 8 классе по теме:
«Площади. Теорема Пифагора.»
Разработка учителя математики
I категории
Илясовой Галины Константиновны
г. Майкоп
2015 год
Урок обобщения по теме:
«Площади. Теорема Пифагора»
Геометрия 8 класс включает изучение вопросов:
-
“Площадь треугольника”
-
“Площадь параллелограмма”
-
“Площадь трапеции”
-
“Теорема Пифагора”
Основная цель: создать условия для формирования учащимися понятия площади, развития умений вычислять площади фигур, применяя изученные свойства и формулы, а также теорему Пифагора.
Цель урока: создать условия для
-
закрепления знаний, умения и навыков учащихся по теме “Площади”,
-
совершенствования навыков решения задач на применение теоремы Пифагора,
-
обобщения и систематизации теоретических знаний учащихся по теме “Площади” и “Теорема Пифагора”,
-
обобщение понятий: теорема Пифагора; основание, высота, диагонали.
Оборудование урока:
-
Плакат “Площади” (Рисунок 1);

-
Теоретический тест в двух вариантах;
-
Карточки с готовыми чертежами к задачам (устная работа);
-
Конверты с задачами для самостоятельной работы (индивидуальные).
Тип урока: повторительно-обобщающий.
Оргформа: урок-практикум.
Ход урока
I. Организационный момент
-
совместно с учащимися формулируем тему урока;
-
совместно с учащимися ставим задачи урока;
-
определяем основные этапы урока, для этого обратиться к учащимся с вопросами:
какую тему мы изучили?
что нужно знать по темам “Площади”, теорема Пифагора?
каким образом это можно закрепить?
II. Проверка знаний учащихся
1. Проверка теории (учащиеся получают тест).
Вариант 1.
Выбери верные утверждения:
а) Площадь параллелограмма равна:
-
произведению его сторон;
-
произведению его высот;
-
произведению его стороны на высоту, проведенную к данной стороне.
б) Площадь квадрата со стороной 3см равна:
-
6 см2;
-
8 см;
-
9 см2.
в) Закончите предложение: “Площадь ромба равна…
-
произведению его сторон;
-
половине произведения его диагоналей;
-
произведению его стороны и высоты.
г) По формуле ![]() можно вычислить:
можно вычислить:
-
площадь треугольника;
-
площадь прямоугольника;
-
площадь параллелограмма.
д) Площадь трапеции АВСД с основаниями АВ и СД и высотой ВО вычисляется по формуле:

е) Теорема Пифагора утверждает, что в прямоугольном треугольнике:
-
квадрат гипотенузы равен квадрату катета;
-
квадрат гипотенузы равен сумме квадратов катетов;
-
сумма квадратов катетов равна гипотенузе.
Вариант 2.
Выберите верные утверждения:
а) Площадь квадрата равна:
-
произведению его сторон;
-
квадрату его стороны;
-
произведению его сторон на высоту.
б) Площадь параллелограмма равна:
-
произведению его смежных сторон;
-
произведению его высоты на сторону;
-
произведению его основания на высоту, проведенную к данному основанию.
в) По формуле S=d*d /2 можно вычислить площадь:
-
ромба;
-
треугольника;
-
параллелограмма.
г) Площадь треугольника равна половине произведения:
-
оснований;
-
основания на высоту, проведенную к данному основанию;
-
его высот.
д) Площадь трапеции АВСД с основаниями ВС и АД и высотой ВН равна
-
S=(AB+CD)/2*BH;
-
S=(AD+BC)/2/BH;
-
S=(BC+AD)/2*BH.
е) Теорема Пифагора утверждает, что в прямоугольном треугольнике:
-
квадрат катета равен квадрату гипотенузы;
-
квадрат гипотенузы равен сумме квадратов катетов;
-
сумма квадратов катетов равна гипотенузе.
Учащиеся ставят знак + в выбранном ответе. По таблице ответов проводят взаимоконтроль в парах.
Таблица ответов:
| а | б | в | г | д | е | |
| 1 | 3 | 3 | 3 | 1 | 3 | 2 |
| 2 | 2 | 3 | 1 | 2 | 3 | 2 |
2. Решение задач по готовым чертежам.
а) Решите устно, найдите площади фигур:
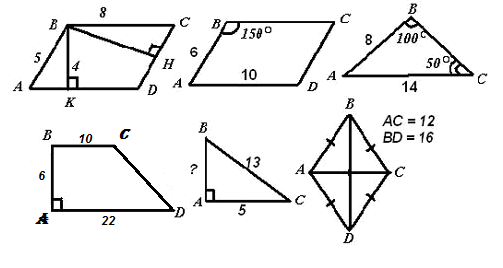
3. Решение задач письменно в тетрадях с последующей самопроверкой (по вариантам)
Вариант 1.
Дано: АВСD – трапеция; ВС : АD = 2 : 3; ВК = 6; SABCD = 60. Найти: BC, AD

Вариант 2.
Дано: ![]() ABC;
ABC; ![]() A =
A = ![]() C = 75°; АВ = 12. Найти: S
C = 75°; АВ = 12. Найти: S![]() ABC
ABC

Решения:
Вариант 1.
Дано: АВСD – трапеция; ВС : АD = 2 : 3; ВК = 6; SABCD = 60.
Найти: BC, AD

Решение:
Пусть х - коэффициент пропорциональности. Тогда ВС=2х, АD=3х.
По условию SABCD = 60, получим ![]() , 60 = 15х, х = 4,
, 60 = 15х, х = 4,
значит ВС = 2*4=8, AD = 3*4=12.
Ответ: ВС = 8, AD = 12.
Вариант 2.
Дано: ![]() ABC;
ABC; ![]() A =
A = ![]() C = 75°; АВ = 12. Найти: S
C = 75°; АВ = 12. Найти: S![]() ABC
ABC
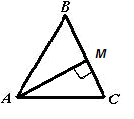
Решение: ![]() ABC;
ABC; ![]() A =
A = ![]() C= 75°,
C= 75°, ![]() В = 30°.
В = 30°.
АВ = ВС = 12 см.
Проведем АМ ┴ ВС. Рассмотрим ![]() ABМ:
ABМ: ![]() М = 90°,
М = 90°, ![]() В = 30°, значит АМ =
В = 30°, значит АМ = ![]() АВ = 6.
АВ = 6.
S![]() ABC =
ABC = ![]() АМ * ВС =
АМ * ВС = ![]() * 6 * 12 = 36.
* 6 * 12 = 36.
Ответ: 36.
Ответы:
-
Вариант 1 ВС=8, AD=12;
-
Вариант-2 SABC=36
4. Самостоятельная работа. (Каждый учащийся получает конверт с задачами 2-х уровней и сам выбирает задание на основе своего уровня подготовки).
Критерий оценки:
-
1 уровень – “3” - №1; “4” - №1, №2.
-
2 уровень – “4” - №1; “5” - №1, №2.
1 уровень
| Вариант 2 | |
| 1. Диагонали ромба 12 см и 16 см Найти сторону ромба | 1. Стороны прямоугольника 5 см и 12 см. Найти диагональ прямоугольника. |
| 2. Найдите площадь равностороннего треугольника, сторона которого равна 12 см. | 2. Стороны AB и BC |
2 уровень
| 1. В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание 20 см. Найти площадь трапеции. | |
| 2. Высота ВK ромба АВСD делит сторону АD на отрезки АК=6 см. и KD=4 см. Найти площадь ромба и его диагонали. | 2. Диагонали ромба равны 18 и 24 см. Найти периметр ромба и расстояние между параллельными сторонами. |
Взаимопроверка работ в парах (готовое решение на доске). (См. Приложение 1).
III. Рефлексия (подведение итогов урока)
-
Чему вы научились при изучении темы раздела;
-
Какими навыками, умениями овладели;
-
Какими формулами, понятиями воспользовались при решении задач?
-
Решение каких задач показалось вам сложным?
-
Какие вопросы требуется вашего особого внимания?
-
Какие задачи вам понравилось решать?
IV. Домашние задание
-
Всем учащимся: Стр. 133 (1-10) № 503;
-
Дополнительно: № 518 а) (с.135)
Здесь представлен конспект к уроку на тему «Площади. Теорема Пифагора», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

