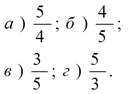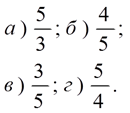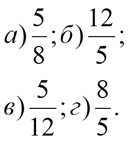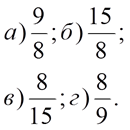Конспект урока «Соотношение между сторонами и углами прямоугольного треугольника» по геометрии для 8 класса
«Соотношение между сторонами и углами прямоугольного треугольника»
Цели урока:
-
образовательная:
обобщить понятия синус, косинус, тангенс острого угла в прямоугольном треугольнике, исследовать зависимости и соотношения между этими величинами; формирование умений и навыков в применении соотношений между сторонами и углами прямоугольного треугольника; формирование умений работать с задачей.
Познавательный аспект: уметь приобретать новые знания, используя различные подходы.
-
развивающая:
развитие памяти, мышления, наблюдательности, внимательности; развитие познавательного интереса; развитие познавательных и исследовательских умений учащихся, повышение культуры общения; развитие математической речи учащихся в процессе выполнения устной работы по воспроизведению теоретического материала; развитие у школьников самостоятельности мышления.
-
воспитательная:
воспитание самостоятельности, аккуратности, умения отстаивать свою точку зрения, умения выслушать других, способствовать повышению активности учащихся на уроке, повышению грамотности устной и письменной речи.
Тип урока: комбинированный.
Формы организации познавательной деятельности: Фронтальная, индивидуальная, групповая .
Оборудование: тестовые работы, презентация (при наличии необходимого оборудования), карточки для блиц- опроса, модели треугольников.
| Этапы урока | Время | |
| 1. | Организационный момент. | 2 |
| 2. | Сообщение темы и целей урока | 2-3 |
| 3. | Воспроизведение опорных знаний | 10 |
| 4. | Повторение изученного материала | 5 |
| 5. | Решение задач | 15 |
| 6. | Рефлексия. | 2-3 |
| 7. | Подведение итогов. Выставление оценок | 3-4 |
| 8. | Постановка домашнего задания | 2-3 |
| | ||
Эпиграф:
Не стыдно чего-нибудь не знать,
но стыдно не хотеть учиться (Сократа)
Ход урока
1. Организационный момент.
2.Сообщение темы и целей урока
Учитель: мы заканчиваем изучение темы «Соотношения между сторонами и углами треугольника», сегодня мы проводим обобщающий урок по этой теме и основной целью нашего урока является – систематизация и обобщение знаний учащихся.
Мотивация урока. (слайд 1)
Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная…»
У вас может возникнуть вопрос: Почему в геометрии особое внимание уделяется прямоугольному треугольнику, хотя не часто встречаются предметы подобной формы?
Как в химии изучают вначале элементы, а затем – их соединения, в биологии – одноклеточные, а потом – многоклеточные организмы, так и в геометрии – точки, отрезки и треугольники, из которых состоят другие геометрические фигуры.
Среди этих фигур прямоугольный треугольник играет особую роль. Действительно, любой многоугольник можно разбить на треугольники, умея находить угловые и линейные элементы этих треугольников, можно найти все элементы многоугольника. В свою очередь, любой треугольник можно разбить одной из его высот на два прямоугольных треугольника, элементы которых связаны более простой зависимостью. Найти элементы треугольника можно. Если свести задачу к решению этих двух прямоугольных треугольников.
3. Воспроизведение опорных знаний
Блиц – опрос (слайд № 2)
| ( слайд № 3) | |
| Вариант 1 | Вариант 2 |
| 1.Закончите предложение: «Косинусом острого угла прямоугольного треугольника называется отношение…» | 1.Закончите предложение: «Синусом острого угла прямоугольного треугольника называется отношение…» |
| 2.Закончите предложение: «Тангенсом острого угла прямоугольного треугольника называется отношение…» | 2. Закончите предложение: «Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то…» |
| 3. Запишите, используя обозначения косинус 60° равен | 3. Запишите, используя обозначения синус 45°равен |
| 4.Запишите основное тригонометрическое тождество | 4. Запишите формулой, чему равен тангенс угла А |
| 5. Может ли синус острого угла равняться 1,01? | 5. Тангенс острого угла прямоугольного треугольника равен единице. Какого вида этот треугольник? |
| Чему равен? | Чему равен? |
| 6. Sin 60° | 6. Cos 30° |
| 7. Cos 45° | 7. Sin 45° |
| 8. Tg 60° | 8. Tg 30° |
(слайд №4)
| Ответы | |
| 1…прилежащего катета к гипотенузе; | 1…противолежащего катета к гипотенузе; |
| 2…противолежащего катета к прилежащему; | 2…синусы, косинусы, тангенсы этих углов также равны; |
| 3. cos60°=1/2; | 3. sin45°= |
| 4. sin2A + cos2A = 1; | 4. |
| 5. Нет; | 5. равнобедренный; |
| 6. | 6. |
| 7. | 7. |
| 8. | 8. |
4. Повторение изученного материала
Вспомним содержание основных задач на решение прямоугольных треугольников. Решение данных задач основано на теореме Пифагора и понятиях sin a, cos а, tg а
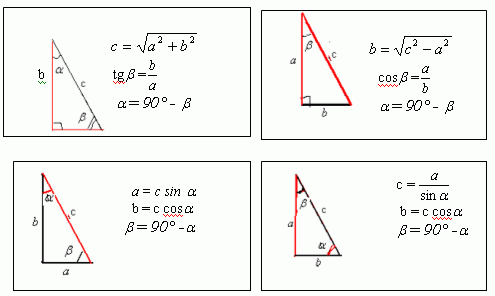
5. Решение задач
Решение многих прикладных задач основано на решении прямоугольных треугольников.
Рассмотрим некоторые виды прикладных задач.
-
Задачи на нахождение высоты предмета, основание которого доступно.
-
Задачи на нахождение высоты предмета, основание которого недоступно.
-
Задачи на нахождение расстояния между двумя пунктами, которые разделяет препятствие.
-
Задачи на нахождение углов.
Задача. Насыпь шоссейной дороги имеет в верхней части ширину 60 м. Какова ширина насыпи в нижней её части, если угол наклона откосов к горизонту равен 60°, а высота насыпи равна 12 м.( учебник № 600 ) ( слайд № 7)

Решение исторических задач. ( слайд №8)

( слайд № 9)

( слайд № 10)
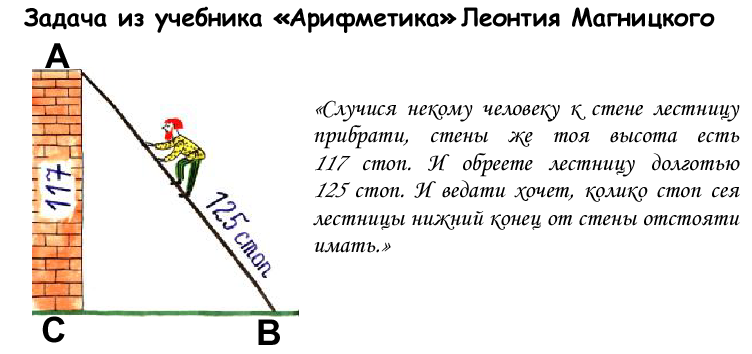
-
Самостоятельная работа. ( слайд № 12)
Раздаем карточки
| Вариант 2 | |
| 1.Найдите синус угла А АВС,угол С=90°, если ВС=4, АВ= 5.
| 1.Найдите косинус углаВАВС, угол С=90°, если ВС=3, АВ= 5
|
| 1. | 2. |
| 3. Дано:АВС, ВС=5см угол С=90°,угол А=41° Найти: АС а) 5* cos41°; б) 5:tg41°; с) 5* tg41°; г) 5: sin41°. |
Найти: АС а) 9: tg49°; б) 9*cos49°; в) 9: sin49°; г) 9* tg49°. |
| 4. а) -2,25; б) -1,25; в) -0,75; г) -1,5. | 4. а) -2; б) -3; в) -1,5; г) -2,5. |
6.Рефлексия. ( слайд № 13)
-
Трудным ли для тебя был материал урока?
-
На каком из этапов урока было труднее всего, легче всего?
-
Работал ли ты на уроке в полную меру сил?
-
Как эмоционально ты чувствовал себя на уроке?
7.Подведение итогов. Выставление оценок
8. Домашнее задание. (слайд № 14)
Письменно № 599,602
Повторить п. 66, 67.
– Спасибо урок окончен. До свидания! ( слайд № 15)
Используемая литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 7-9: учеб. Для общеобразоват. учреждений. – 18-е изд. – М.:Просвещение, 2008.
Изучение геометрии в 7-9 классах: Методические рекомендации; Кн. Для учителя / Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. – М.:Просвещение, 1997.
Гаврилова Н.Ф. Поурочные разработки по геометрии, 8 класс – М.: «ВАКО», 2004.
Электронная поддержка урока:
Авторская презентация «Соотношения между сторонами и углами прямоугольного треугольника»
Подсказка ученикам, лучше раздать каждому
-
Условие задачи
Алгоритм решения
1
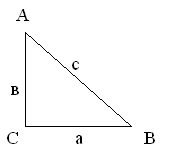
Дано: АС=в, ВС=а.
Найти: АВ,
1)АВ=
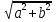 ,
,2) tgА=
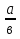 ;
;3)
2

Дано: АВ=с, ВС=а.
Найти: АС,
1)АС=
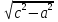 ,
,2)
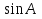 =
=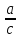 ;
;3)
3

Дано: АВ=с,
Найти: АС,ВС,
-
АС=с·cosα,
-
ВС=с·sinα.
4

Дано:
Найти: АС, АВ,
-
АВ=
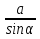 ,
, -
АС=
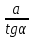 .
.
Здесь представлен конспект к уроку на тему «Соотношение между сторонами и углами прямоугольного треугольника», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.