Конспект урока «Соотношения между сторонами и углами прямоугольного треугольника» по геометрии
Оноприенко Л.Н.;
учитель математики ШЛ №27
(из опыта работы).
Урок по теме: Соотношения между сторонами и углами прямоугольного треугольника.
Тип урока: Урок решение задач.
Цель урока: Применение знаний, умений и навыков по теме "Соотношения между сторонами и углами прямоугольного треугольника" к решению задач прикладного характера.
Задачи урока:
1) Повторить базовые знания по теме.
Показать их применение к решению прикладных и практических задач.
2) Воспитать: ответственность, активность, инициативу и творческий
подход к делу, дух соревновательности.
3) Развивать: Практические умения и навыки, элементы моделирования
и конструирования, поисково-исследовательскую деятельность,
логическое мышление, вычислительные навыки, геометрическое видение.
Метод: Практический с элементами моделирования и конструирования, частично-поисковой деятельностью.
Средства:
-
Интерактивная доска.
-
Тест по теме " Теорема Пифагора" (логические цепочки в задачах на готовых чертежах).
-
Инструкция по выполнению теста.
-
Таблицы с задачами на готовых чертежах.
5) Карточки с задачами прикладного и практического характера.
6) Классмейты, таблицы Брадиса.
7) Презентация исторического материала " О значении теоремы Пифагора."
8) Набор инструментов для построения прямого угла.
9) Оценочный лист.
План урока.
1.Организационный момент. Постановка цели урока.
2.Проверка базовых знаний и умений по теме: "Решение прямоугольных треугольников"
а) Ребусы ( на повторение основных понятий )
б) Работа по готовым чертежам.
в) Практическая работа по построению прямого угла.
3. Тест по теме " Теорема Пифагора" ( логические цепочки в задачах на готовых
чертежах.)
4.Решение прикладных и практических задач.
5. Исторический экскурс (о значении теоремы Пифагора )
6. Подведение итогов урока.
Выставление оценок.
Рефлексия.
7. Постановка домашнего задания.
Перед уроком на интерактивной доске демонстрируется слаид-шоу фрагментов красивейших архитектурных сооружений столицы.
Начинается урок. Учитель просит ребят прокомментировать увиденный сюжет и дать ему название. Затем говорит о том, что уже очень многое изучено по треугольнику в том числе по прямоугольному и объявляет конкурс на лучшую презентацию мини-проекта "Астана в геометрических образах".
Главный сюжет - пространственный аналог треугольника: треугольная пирамида в архитектурных сооружениях города Астаны. Срок-1месяц.
Х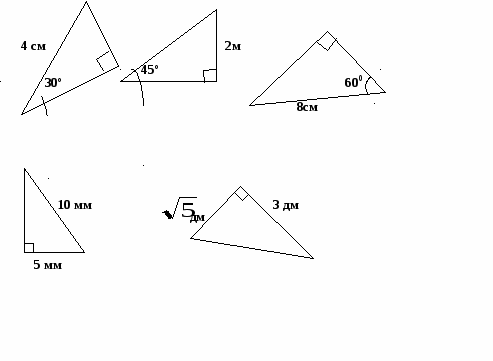 од урока.
од урока.
| Содержание учебного материала. | Деятельность учителя и ученика. | |
| 1. | Организационный момент. Постановка цели урока. Тема: Соотношения между сторонами и углами прямоугольного треугольника. Цель урока: Применение знаний, умений и навыков по теме "Соотношения между сторонами и углами прямоугольного треугольника" к решению задач прикладного и практического характера. | Проверяет готовность класса к уроку, объявляет цель урока. |
| 2. | Проверка базовых знаний и умений по теме: "Решение прямоугольных треугольников" а) Разгадать ребусы (на повторение основных понятий). ( Приложение 1). Землемеры древнего Египта для построения прямого угла использовали бечевку, разделенную узлами на двенадцать равных частей. Покажите. как они это делали. Указание: в углах должны быть узлы. | На интерактивной доске. Фронтальная работа. Параллельно с фронтальной работой группа учащихся из трёх человек выполняет практическую работу по построению прямого угла; затем перед классом демонстрируют результат, делают обоснование, используя обратную теорему Пифагора. |
| | б) работа по готовым чертежам:
( Взаимно обратные задачи; используются пифагоровы тройки). | На интерактивной доске. Устная фронтальная работа оценивается жетонами. |
|
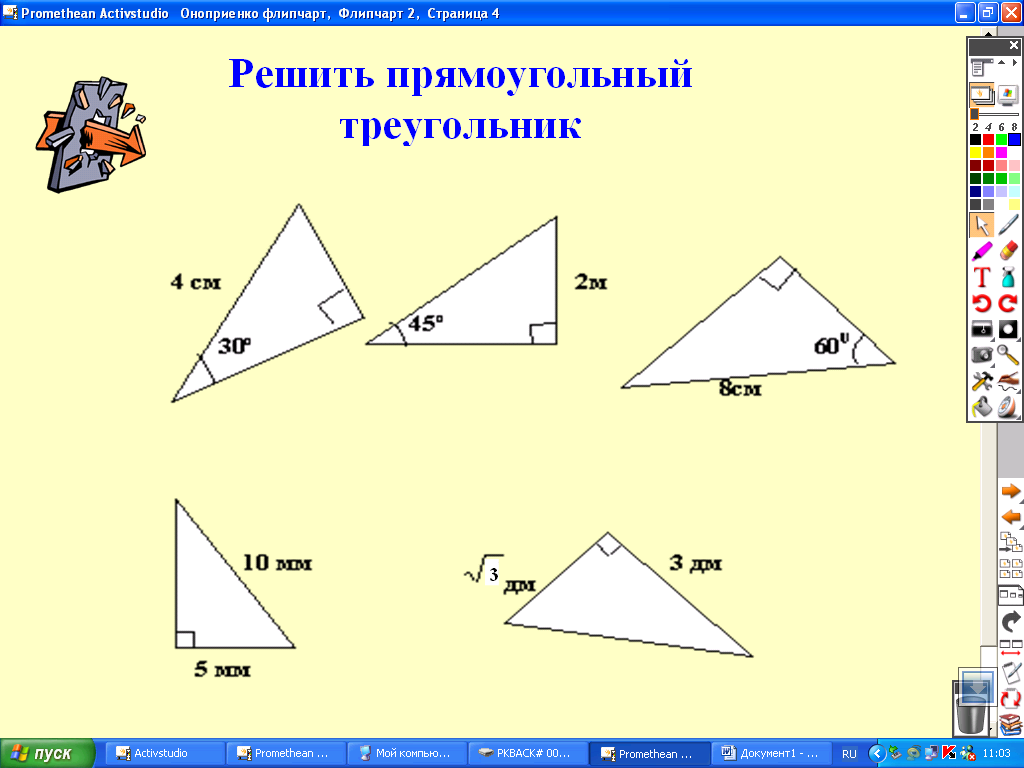
| 2) Решить прямоугольный треугольник Подводится итог работы по проверки базовых знаний | Учитель перед началом работы задает вопросы:
а) теорема Пифагора б) значения sin, cos, tg,ctg острых углов прямоугольного треугольника в) теорема о сумме углов треугольника 3. Определяется ли однозначно треугольник по углам По оценочному листу |
| 3 | Инструкция по выполнению теста:
Задание 1-4 см. приложения 2 Самооценка по критериям указаным в оценочном листе ( приложение 3) | Логические цепочки в задачах на готовых чертежах (тесты по теме: «Теорема Пифагора»). Каждой паре учащихся на стол выкладывается инструкция по выполнению теста. (работа в парах) Каждой паре учащихся дается таблица с комбинацией прямоугольных треугольников и инструкция по выполнению задания. Проверка идет на интерактивной доске, учащиеся вписывают верные ответы в пустые квадратики, параллельно с доской идет самоконтроль и самооценка. Ответ записывается на карточку каждым учеником в виде четверки чисел. Записывается количество верных ответов. |
| 4
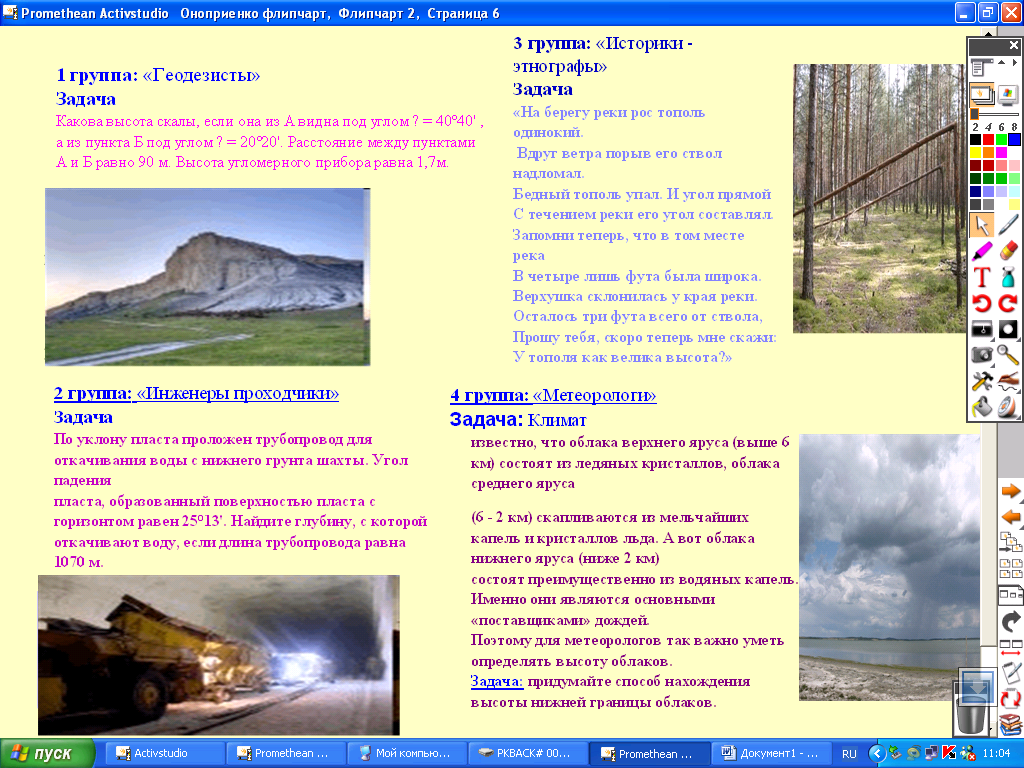
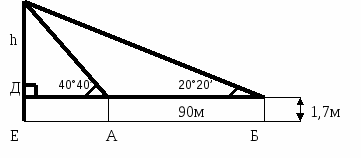
| Решение прикладных и практических задач. 1 группа: «Геодезисты» Задача Какова высота скалы, если она из А видна под углом α = 40°40’, а из пункта Б под углом β = 20°20’. Расстояние между пунктами А и Б равно 90 м. Высота угломерного прибора равна 1,7м. Ответ: 60,3 м 2 группа: «Инженеры проходчики» Задача По уклону пласта проложен трубопровод для откачивания воды с нижнего грунта шахты. Угол падения пласта, образованный поверхностью пласта с горизонтом равен 25°13’. Найдите глубину, с которой откачивают воду, если длина трубопровода равна 1070 м.
3 группа: «Историки - этнографы» Задача «На берегу реки рос тополь одинокий. В Бедный тополь упал. И угол прямой С течением реки его угол составлял. Запомни теперь, что в том месте река В четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?» 4 группа: «Метеорологи» Задача: Климат известно, что облака верхнего яруса (выше 6 км) состоят из ледяных кристаллов, облака среднего яруса ( Задача: придумайте способ нахождения высоты нижней границы облаков. | Рисунки проецируются на интерактивную доску. Класс разбит на четыре микрогруппы: каждая группа ребят – представители одной из «Профессии» (геодезисты, инженеры проходчики, географы – метеорологи, этнографы-историки). Каждой группе в зависимости от их профиля дается прикладная или практическая задача, решить которую необходимо за 8 минут. Ученики:
Работа выполняется каждым учеником группы в тетради. Учитель: направляет работу учеников. Защита: от каждой группы представитель объясняет решение, дает обоснование. Группа оценивается учителем и учениками, результаты выставляются в оценочный лист |
| 5 | Информационно-обобщающий. О значении теоремы Пифагора: Оказывается, за долго до Пифагора она была известна египтянам, вавилонянам, китайцам и индийцам. Индийцы использовали ее для построения алтарей, которые по священному предписанию должны иметь геометрическую форму, ориентированную относительно четырех сторон горизонта. Доказательство самого Пифагора до нас не дошло. В настоящее время имеется более ста различных доказательств этой теоремы. Значение теоремы состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Доказательство теоремы учащиеся средних веков считали очень трудным и называли его «Ослиный мост» или «Бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, «бежали» от геометрии. Ученики рисовали шаржи на теорему Пифагора. Существует легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков. Поэты сочиняли стихи об этой теореме. Например, А. Шамиссо писал: Прибудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора, верна Как и его далекий век! | Двое учащихся заранее готовит сообщение. Теорема Пифагора – одна из главных теорем геометрии. Рассказ учащихся сопровождается показом слайдов ( см. приложение 1-5 Учитель благодарит учеников за содержательную информацию. |
| 6 | Подведение итогов урока а) какие знания нам понадобились при решении задач данного типа? б) о чем надо помнить, применяя теорему Пифагора? в) достигли ли мы цели урока? Самооценка по основным видам работ (см. оценочный лист | Учитель дает общую оценку работе на уроке. Выставляет отметки Оценочный лист |
| 7 | Постановка домашнего задания
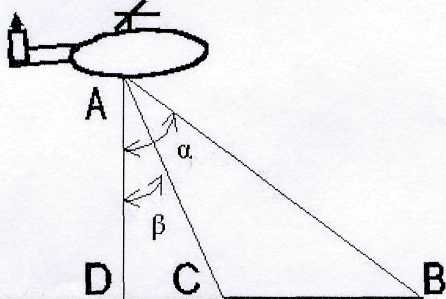
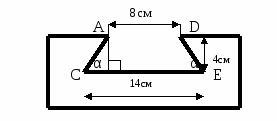
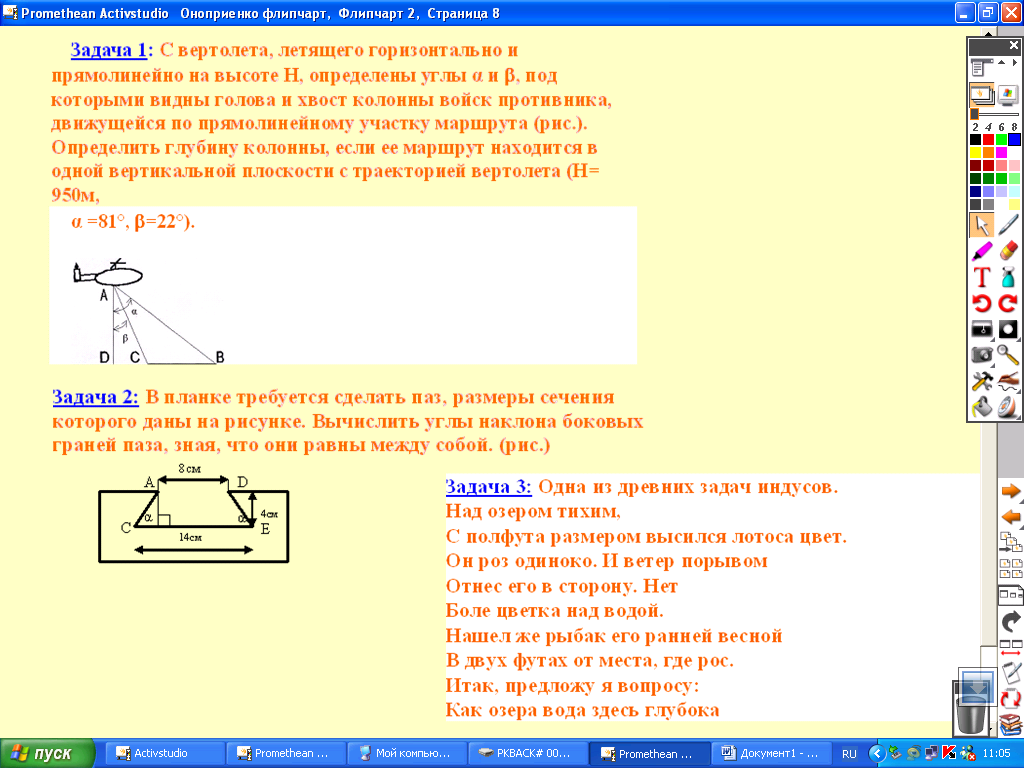
Задача 1: С вертолета, летящего горизонтально и прямолинейно на высоте Н, определены углы α и , под которыми видны голова и хвост колонны войск противника, движущейся по прямолинейному участку маршрута (рис. 8). Определить глубину колонны, если ее маршрут находится в одной вертикальной плоскости с траекторией вертолета (Н= 950м, α =81°, =22°). Задача 2: В планке требуется сделать паз, размеры сечения которого даны на рисунке. Вычислить углы наклона боковых граней паза, зная, что они равны между собой. (рис.)
Задача 3: Одна из древних задач индусов. Над озером тихим, С полфута размером высился лотоса цвет. Он роз одиноко. И ветер порывом Отнес его в сторону. Нет Боле цветка над водой. Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопросу: Как озера вода здесь глубока Урок завершается вручением каждому ученику небольшого сюрприза: открытка с одним из пожеланий:
| Учитель объявляет конкурс на лучшую презентацию мини-проекта (пространственные аналоги треугольника). Предложенные задачи прикладного характера должен решить каждый ученик, оформив решение в тетради. Учитель демонстрирует условие каждой задачи на интерактивной доске. Каждый ученик получает карточки с домашним зданием Открытки с сюрпризом вручаются каждому ученику. |
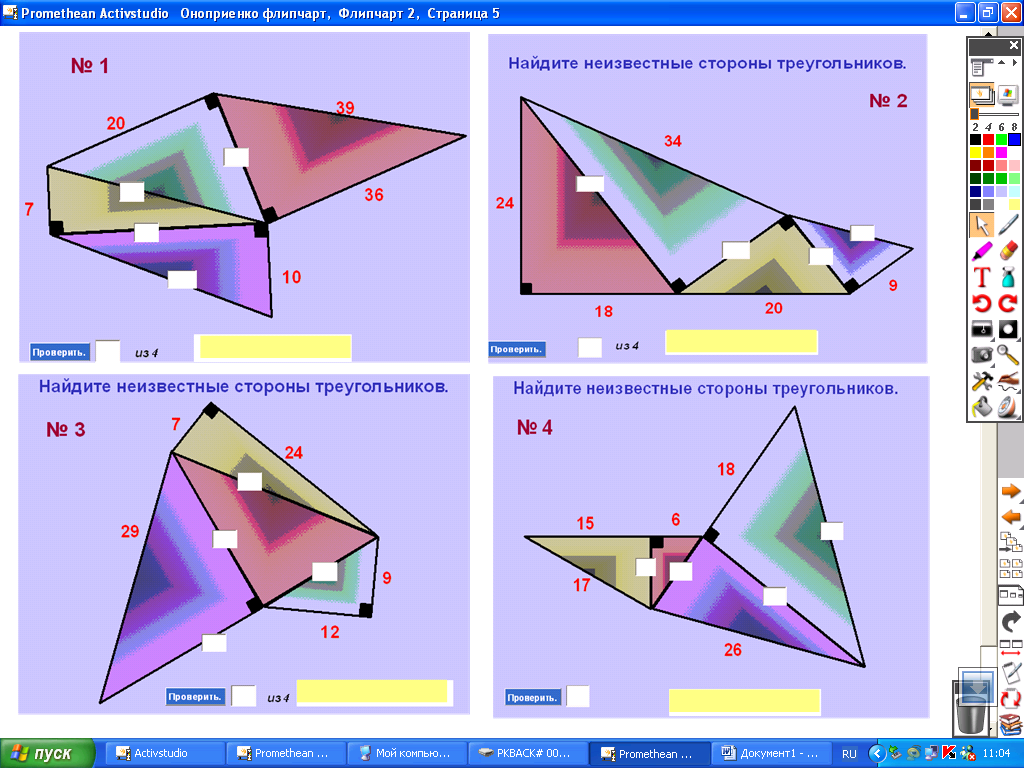
Приложение 2
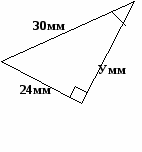
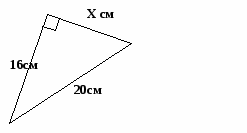
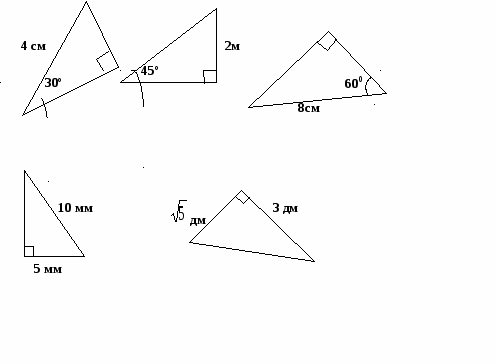
Найдите неизвестные стороны треугольников.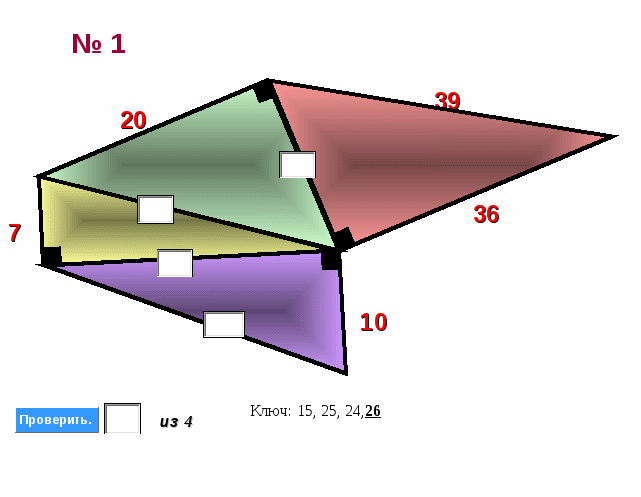

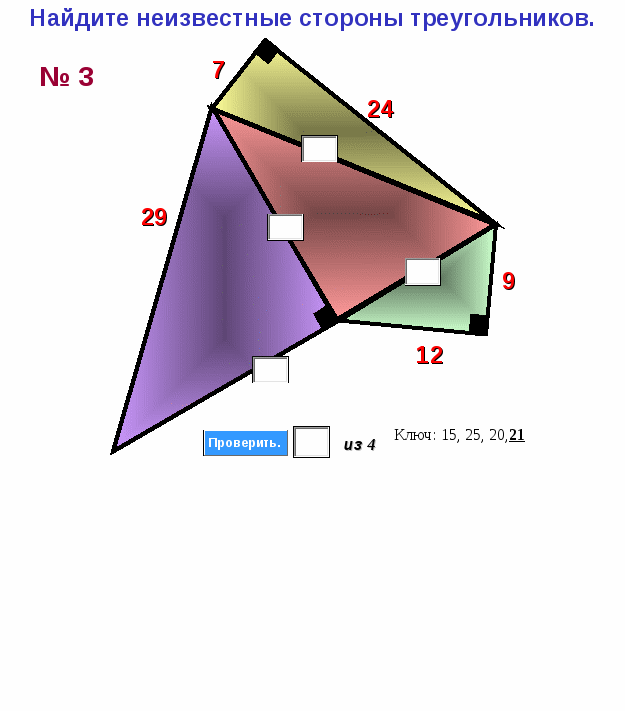
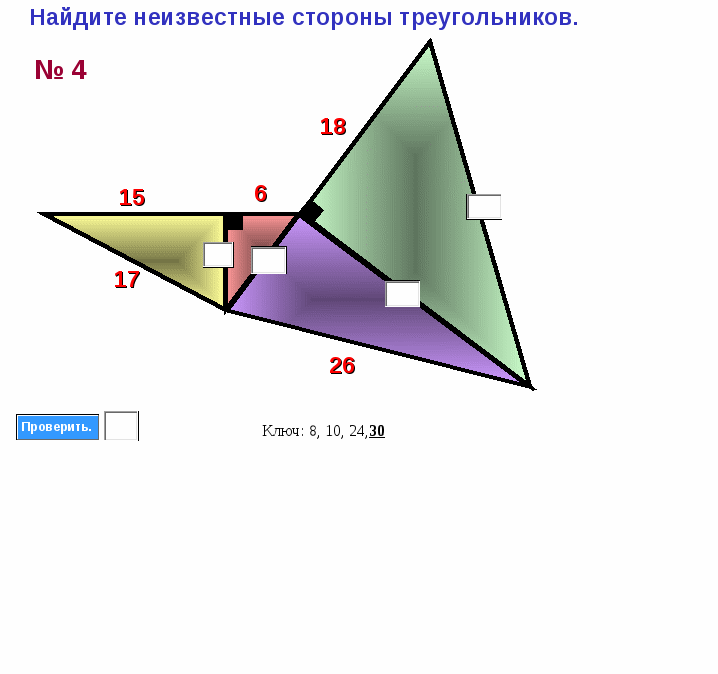
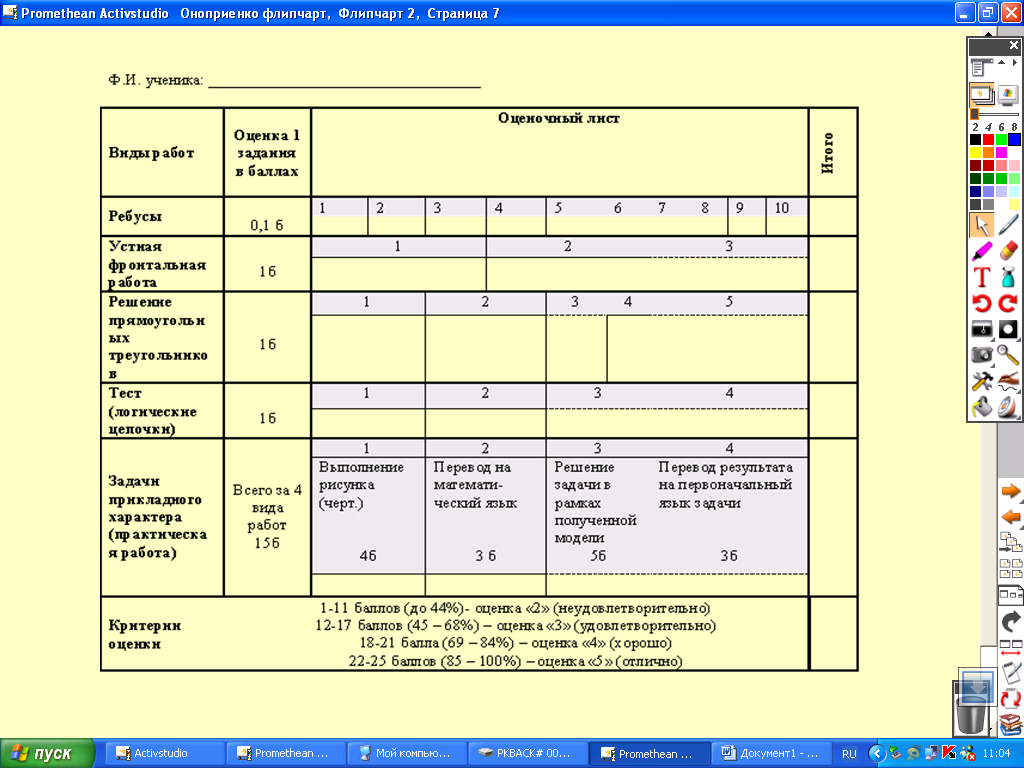
Приложение 3
Ф.И. ученика: __________________________________
| Оценка 1 задания в баллах | Оценочный лист | Итого | ||||||||||
| Ребусы | 0,1 б | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| | | | | | | | | | | |||
| Устная фронтальная работа | 1б | 1 | 2 | 3 | | |||||||
| | | | ||||||||||
| Решение прямоугольных треугольников | 1б | 1 | 2 | 3 | 4 | 5 | | |||||
| | | | | | ||||||||
| Тест (логические цепочки) | 1б | 1 | 2 | 3 | 4 | | ||||||
| | | | | |||||||||
| Задачи прикладного характера (практическая работа) | Всего за 4 вида работ 15б | 1 | 2 | 3 | 4 | | ||||||
| Выполнение рисунка (черт.) | Перевод на математи-ческий язык | Решение задачи в рамках полученной модели | Перевод результата на первоначальный язык задачи | |||||||||
| 4б | 3 б | 5б | 3б | |||||||||
| | | | | |||||||||
| Критерии оценки | 1-11 баллов (до 44%)- оценка «2» (неудовлетворительно) 12-17 баллов (45 – 68%) – оценка «3» (удовлетворительно) 18-21 балла (69 – 84%) – оценка «4» (хорошо) 22-25 баллов (85 – 100%) – оценка «5» (отлично) | | ||||||||||


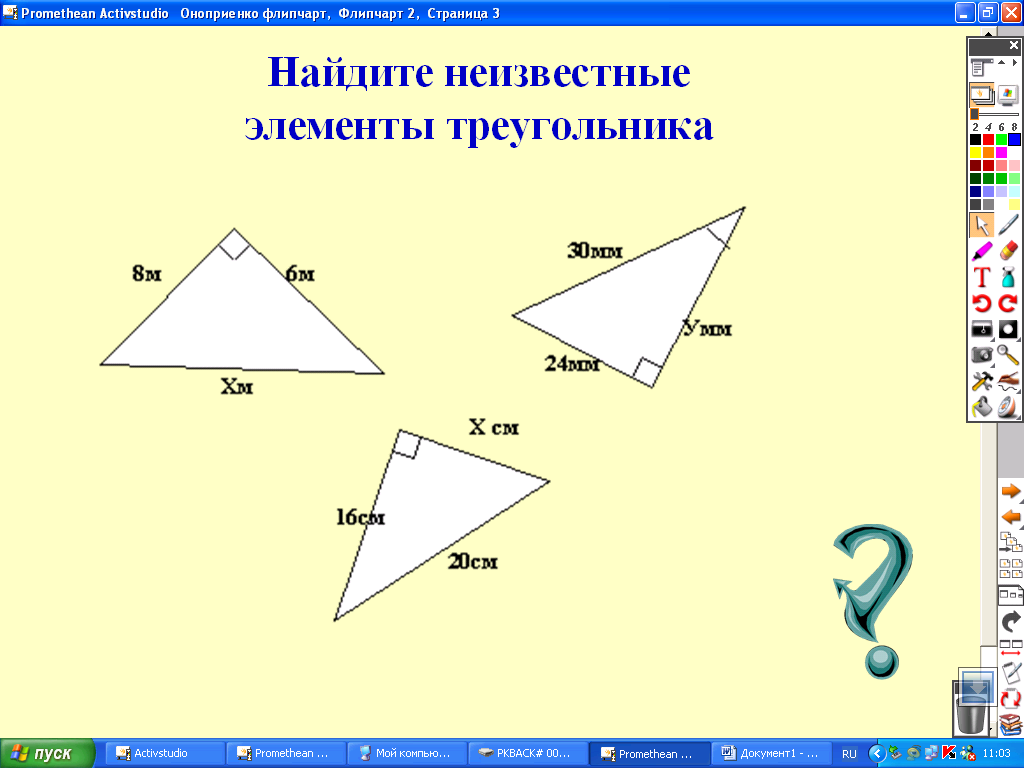
Здесь представлен конспект к уроку на тему «Соотношения между сторонами и углами прямоугольного треугольника», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

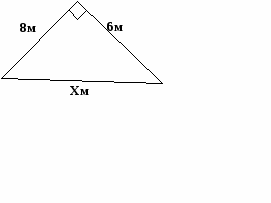
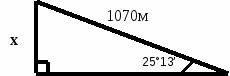
 друг ветра порыв его ствол надломал.
друг ветра порыв его ствол надломал.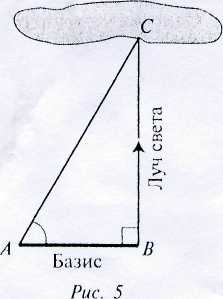 6 – 2 км) скапливаются из мельчайших капель и кристаллов льда. А вот облака нижнего яруса (ниже 2 км) состоят преимущественно из водяных капель. Именно они являются основными «поставщиками» дождей. Поэтому для метеорологов так важно уметь определять высоту облаков.
6 – 2 км) скапливаются из мельчайших капель и кристаллов льда. А вот облака нижнего яруса (ниже 2 км) состоят преимущественно из водяных капель. Именно они являются основными «поставщиками» дождей. Поэтому для метеорологов так важно уметь определять высоту облаков.