Тест «Сокращение дробей. Сравнение, сложение и вычитание дробей с разными знаменателями» по математике
Тест по теме «НОД и НОК» Фамилия, Имя ____________________________________________
-
Натуральные числа называются взаимно простыми, если:
а) у них более двух делителей; б) их НОД равен 1; в) у них один делитель.
-
Наибольшим общим делителем чисел а и в называется:
а) наибольшее натуральное число, на которое делятся без остатка эти числа;
б) наименьшее натуральное число, которое кратно и а, и в;
в) наибольшее натуральное число, которое делится без остатка на эти числа.
-
Наименьшим общим кратным чисел а и в называется:
а) наибольшее натуральное число, на которое делятся без остатка эти числа;
б) наименьшее натуральное число, которое делится без остатка на эти числа;
в) наименьшее натуральное число, которое кратно и а, и в.
-
Чтобы найти НОК нескольких натуральных чисел, надо:
а) Разложить их на простые множители. Выписать множители, входящие в разложение одного из чисел; добавить к ним недостающие множители из разложения остальных чисел. Найти произведение получившихся множителей.
б) Разложить их на простые множители. Выписать множители, входящие в разложение одного из чисел; добавить к ним все множители из разложения остальных чисел. Найти произведение получившихся множителей.
в) Разложить их на простые множители. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел. Найти произведение оставшихся множителей.
-
Чтобы найти НОД нескольких натуральных чисел, надо:
а) Разложить их на простые множители. Выписать множители, входящие в разложение одного из чисел; добавить к ним недостающие множители из разложения остальных чисел. Найти произведение получившихся множителей.
б) Разложить их на простые множители. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые входят в разложение других чисел. Найти произведение получившихся множителей.
в) Разложить их на простые множители. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел. Найти произведение оставшихся множителей.
Тест по теме «НОД и НОК» Фамилия, Имя _____________________________________________
-
Натуральные числа называются взаимно простыми, если:
а) у них более двух делителей; б) их НОД равен 1; в) у них один делитель.
-
Наибольшим общим делителем чисел а и в называется:
а) наибольшее натуральное число, на которое делятся без остатка эти числа;
б) наименьшее натуральное число, которое кратно и а, и в;
в) наибольшее натуральное число, которое делится без остатка на эти числа.
-
Наименьшим общим кратным чисел а и в называется:
а) наибольшее натуральное число, на которое делятся без остатка эти числа;
б) наименьшее натуральное число, которое делится без остатка на эти числа;
в) наименьшее натуральное число, которое кратно и а, и в.
-
Чтобы найти НОК нескольких натуральных чисел, надо:
а) Разложить их на простые множители. Выписать множители, входящие в разложение одного из чисел; добавить к ним недостающие множители из разложения остальных чисел. Найти произведение получившихся множителей.
б) Разложить их на простые множители. Выписать множители, входящие в разложение одного из чисел; добавить к ним все множители из разложения остальных чисел. Найти произведение получившихся множителей.
в) Разложить их на простые множители. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел. Найти произведение оставшихся множителей.
-
Чтобы найти НОД нескольких натуральных чисел, надо:
а) Разложить их на простые множители. Выписать множители, входящие в разложение одного из чисел; добавить к ним недостающие множители из разложения остальных чисел. Найти произведение получившихся множителей.
б) Разложить их на простые множители. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые входят в разложение других чисел. Найти произведение получившихся множителей.
в) Разложить их на простые множители. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел. Найти произведение оставшихся множителей.
Тест по теме «Сокращение дробей. Сравнение, сложение и вычитание дробей с разными знаменателями»
Фамилия, Имя ___________________________________________
1. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится:
а) дробь, противоположная данной; б) более двух делителей; в) равная ей дробь.
-
Наименьший общий знаменатель должен:
а) быть делителем данных дробей;
б) делиться на знаменатели данных дробей без остатка;
в) делиться на знаменатели данных дробей с остатком.
-
Чтобы привести дробь к наименьшему общему знаменателю, надо:
а) Найти НОК знаменателей этих дробей; умножить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; умножить числитель каждой дроби на дополнительный множитель;
б) Найти НОК знаменателей этих дробей; разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; умножить знаменатель каждой дроби на дополнительный множитель;
в) Найти НОК знаменателей этих дробей; разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; умножить числитель и знаменатель каждой дроби на дополнительный множитель.
4. Чтобы сравнить (сложить или вычесть) дроби с разными знаменателями, надо:
а) привести данные дроби к наименьшему общему знаменателю; сравнить (сложить или вычесть дроби);
б) разложить числитель на простые множители; сравнить (сложить или вычесть дроби);
в) разложить знаменатель на простые множители; сравнить (сложить или вычесть дроби).
Тест по теме «Сокращение дробей. Сравнение, сложение и вычитание дробей с разными знаменателями»
Фамилия, Имя ___________________________________________
1. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится:
а) дробь, противоположная данной; б) более двух делителей; в) равная ей дробь.
-
Наименьший общий знаменатель должен:
а) быть делителем данных дробей;
б) делиться на знаменатели данных дробей без остатка;
в) делиться на знаменатели данных дробей с остатком.
-
Чтобы привести дробь к наименьшему общему знаменателю, надо:
а) Найти НОК знаменателей этих дробей; умножить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; умножить числитель каждой дроби на дополнительный множитель;
б) Найти НОК знаменателей этих дробей; разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; умножить знаменатель каждой дроби на дополнительный множитель;
в) Найти НОК знаменателей этих дробей; разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; умножить числитель и знаменатель каждой дроби на дополнительный множитель.
4. Чтобы сравнить (сложить или вычесть) дроби с разными знаменателями, надо:
а) привести данные дроби к наименьшему общему знаменателю; сравнить (сложить или вычесть дроби);
б) разложить числитель на простые множители; сравнить (сложить или вычесть дроби);
в) разложить знаменатель на простые множители; сравнить (сложить или вычесть дроби).
5. Чтобы сложить смешанные числа, надо:
а) привести дробные части этих чисел к НОЗ; выполнить сложение целых частей и дробных частей вместе. Если при сложении дробных частей получится неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части;
б) привести дробные части этих чисел к НОЗ; отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получится неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части;
в) привести дробные части этих чисел к НОЗ; отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении целых частей получится неправильная дробь, выделить целую часть из этой целой части и прибавить её к полученной дробной части.
6. Чтобы выполнить вычитание смешанных чисел, надо:
а) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей;
б) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить сложение целых частей и отдельно дробных частей;
в) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого больше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей.
5. Чтобы сложить смешанные числа, надо:
а) привести дробные части этих чисел к НОЗ; выполнить сложение целых частей и дробных частей вместе. Если при сложении дробных частей получится неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части;
б) привести дробные части этих чисел к НОЗ; отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получится неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части;
в) привести дробные части этих чисел к НОЗ; отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении целых частей получится неправильная дробь, выделить целую часть из этой целой части и прибавить её к полученной дробной части.
6. Чтобы выполнить вычитание смешанных чисел, надо:
а) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей;
б) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить сложение целых частей и отдельно дробных частей;
в) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого больше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей.
Тест по теме «Применение распределительного свойства умножения»
-
Чтобы умножить дробь на натуральное число, надо:
а) её числитель умножить на это число, а знаменатель оставить без изменения;
б) её знаменатель умножить на это число, а числитель оставить без изменения;
в) её числитель и знаменатель умножить на это число.
-
Чтобы умножить дробь на дробь, надо:
а) найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать знаменателем, а второе – числителем;
б) найти произведение числителей, а знаменатель оставить прежним;
в) найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем;
-
Для того чтобы выполнить умножение смешанных чисел, надо:
а) отдельно умножить целые числа, отдельно дробные;
б) записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Тест по теме «Применение распределительного свойства умножения»
-
Чтобы умножить дробь на натуральное число, надо:
а) её числитель умножить на это число, а знаменатель оставить без изменения;
б) её знаменатель умножить на это число, а числитель оставить без изменения;
в) её числитель и знаменатель умножить на это число.
-
Чтобы умножить дробь на дробь, надо:
а) найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать знаменателем, а второе – числителем;
б) найти произведение числителей, а знаменатель оставить прежним;
в) найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем;
-
Для того чтобы выполнить умножение смешанных чисел, надо:
а) отдельно умножить целые числа, отдельно дробные;
б) записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
-
Чтобы найти дробь от числа, надо:
а) сложить число и эту дробь;
б) умножить число на эту дробь;
в) разделить число на эту дробь.
-
Чтобы умножить смешанное число на натуральное число, можно:
а) умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; сложить полученные результаты;
б) умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; вычесть полученные результаты;
в) умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; умножить полученные результаты;
-
Чтобы найти дробь от числа, надо:
а) сложить число и эту дробь;
б) умножить число на эту дробь;
в) разделить число на эту дробь.
-
Чтобы умножить смешанное число на натуральное число, можно:
а) умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; сложить полученные результаты;
б) умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; вычесть полученные результаты;
в) умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; умножить полученные результаты;
Ф.И._______________________________
Тест по теме «Отношения и пропорции»
-
Отношением двух чисел называют:
а) произведение этих чисел; б) частное этих чисел.
-
Отношение показывает:
а) во сколько раз первое число больше второго или какую часть первое составляет от второго;
б) на сколько первое число больше второго или какую часть второе составляет от первого.
-
Что нужно сделать, если величины измерены разными единицами измерениями?
4. Что называют пропорцией?__________________________________________________
5. Подпишите название членов пропорции: а : в = с : d
6. Запишите основное свойство пропорции: ______________________________________
___________________________________________________________________________
7. Что можно найти, используя основное свойство дроби?__________________________
Ф.И._______________________________
Тест по теме «Отношения и пропорции»
-
Отношением двух чисел называют:
а) произведение этих чисел; б) частное этих чисел.
-
Отношение показывает:
а) во сколько раз первое число больше второго или какую часть первое составляет от второго;
б) на сколько первое число больше второго или какую часть второе составляет от первого.
-
Что нужно сделать, если величины измерены разными единицами измерениями?
4. Что называют пропорцией?__________________________________________________
5. Подпишите название членов пропорции: а : в = с : d
6. Запишите основное свойство пропорции: ______________________________________
___________________________________________________________________________
7. Что можно найти, используя основное свойство дроби?__________________________
8. Новые пропорции верны, если:
а) поменять местами числитель и знаменатель в пропорции;
б) поменять местами средние члены или крайние члены.
9. Две величины называют прямо пропорциональными, если:
а) при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз;
б) при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
10. Две величины называют обратно пропорциональными, если:
а) при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз;
б) при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
8. Новые пропорции верны, если:
а) поменять местами числитель и знаменатель в пропорции;
б) поменять местами средние члены или крайние члены.
9. Две величины называют прямо пропорциональными, если:
а) при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз;
б) при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
10. Две величины называют обратно пропорциональными, если:
а) при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз;
б) при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Ф.И._______________________________
Тест по теме «Положительные и отрицательные числа»
-
Какие числа называются положительными?
а) со знаком «+»; б) со знаком «-».
2. Какие числа называют отрицательными?
а) со знаком «+»; б) со знаком «-».
3. Два числа, отличающиеся друг от друга только знаками, называют:
а) положительными; б) противоположными; в) отрицательными.
4. Любое отрицательное число _______________________ любого положительного.
5. Любое положительное число _______________________ нуля.
6. Любое отрицательное число ________________________ нуля.
7. Из двух отрицательных чисел меньше то, модуль которого___________________ .
8. Чему равна сумма двух противоположных чисел? __________________________ .
Ф.И._______________________________
Тест по теме «Положительные и отрицательные числа»
-
Какие числа называются положительными?
а) со знаком «+»; б) со знаком «-».
2. Какие числа называют отрицательными?
а) со знаком «+»; б) со знаком «-».
3. Два числа, отличающиеся друг от друга только знаками, называют:
а) положительными; б) противоположными; в) отрицательными.
4. Любое отрицательное число _______________________ любого положительного.
5. Любое положительное число _______________________ нуля.
6. Любое отрицательное число ________________________ нуля.
7. Из двух отрицательных чисел меньше то, модуль которого___________________ .
8. Чему равна сумма двух противоположных чисел? __________________________ .
Ф.И._______________________________
Тест по теме «Положительные и отрицательные числа»
-
Какие числа называются положительными?
а) со знаком «+»; б) со знаком «-».
2. Какие числа называют отрицательными?
а) со знаком «+»; б) со знаком «-».
3. Два числа, отличающиеся друг от друга только знаками, называют:
а) положительными; б) противоположными; в) отрицательными.
4. Любое отрицательное число _______________________ любого положительного.
5. Любое положительное число _______________________ нуля.
6. Любое отрицательное число ________________________ нуля.
7. Из двух отрицательных чисел меньше то, модуль которого___________________ .
8. Чему равна сумма двух противоположных чисел? __________________________ .
9. Чтобы сложить два отрицательных числа, надо:
а) из большего модуля слагаемых вычесть меньший; поставить перед полученным числом знак того слагаемого, модуль которого больше;
б) сложить их модули; поставить перед полученным числом знак « - ».
10. Чтобы сложить два числа с разными знаками, надо:
а) из большего модуля слагаемых вычесть меньший; поставить перед полученным числом знак того слагаемого, модуль которого больше;
б) сложить их модули; поставить перед полученным числом знак « - ».
11. Найдите значение суммы:
а) – 36 + (-54)= ; б) -23 + 23= ; в) -145 + 0 = ; г) -127,3 + (-13,9)= ;
д) 26 + (-83)= ; е) ![]() ; ж) -0,28 + 0,18= ; з)
; ж) -0,28 + 0,18= ; з) ![]() + (- 0,4)= .
+ (- 0,4)= .
12. Найдите значение выражения х + 2,6, если: х = -1,47 ___________________________
9. Чтобы сложить два отрицательных числа, надо:
а) из большего модуля слагаемых вычесть меньший; поставить перед полученным числом знак того слагаемого, модуль которого больше;
б) сложить их модули; поставить перед полученным числом знак « - ».
10. Чтобы сложить два числа с разными знаками, надо:
а) из большего модуля слагаемых вычесть меньший; поставить перед полученным числом знак того слагаемого, модуль которого больше;
б) сложить их модули; поставить перед полученным числом знак « - ».
11. Найдите значение суммы:
а) – 36 + (-54)= ; б) -23 + 23= ; в) -145 + 0 = ; г) -127,3 + (-13,9)= ;
д) 26 + (-83)= ; е) ![]() ; ж) -0,28 + 0,18= ; з)
; ж) -0,28 + 0,18= ; з) ![]() + (- 0,4)= .
+ (- 0,4)= .
12. Найдите значение выражения х + 2,6, если: х = -1,47 ___________________________
9. Чтобы сложить два отрицательных числа, надо:
а) из большего модуля слагаемых вычесть меньший; поставить перед полученным числом знак того слагаемого, модуль которого больше;
б) сложить их модули; поставить перед полученным числом знак « - ».
10. Чтобы сложить два числа с разными знаками, надо:
а) из большего модуля слагаемых вычесть меньший; поставить перед полученным числом знак того слагаемого, модуль которого больше;
б) сложить их модули; поставить перед полученным числом знак « - ».
11. Найдите значение суммы:
а) – 36 + (-54)= ; б) -23 + 23= ; в) -145 + 0 = ; г) -127,3 + (-13,9)= ;
д) 26 + (-83)= ; е) ![]() ; ж) -0,28 + 0,18= ; з)
; ж) -0,28 + 0,18= ; з) ![]() + (- 0,4)= .
+ (- 0,4)= .
12. Найдите значение выражения х + 2,6, если: х = -1,47 ___________________________
Ф.И._________________________________
Тест по теме «Умножение и деление положительных и отрицательных чисел»
-
Чтобы перемножить два числа с разными знаками, надо:
а) перемножить модули этих чисел и поставить перед полученным числом знак « - »;
б) перемножить модули этих чисел.
2. Чтобы перемножить два отрицательных числа, надо
а) перемножить модули этих чисел и поставить перед полученным числом знак « - »;
б) перемножить модули этих чисел.
3. Поставьте знак:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4. Чтобы разделить отрицательное число на отрицательное число, надо:
а) разделить модуль делимого на модуль делителя, поставить перед полученным числом знак « - »;
б) разделить модуль делимого на модуль делителя.
Ф.И._________________________________
Тест по теме «Умножение и деление положительных и отрицательных чисел»
-
Чтобы перемножить два числа с разными знаками, надо:
а) перемножить модули этих чисел и поставить перед полученным числом знак « - »;
б) перемножить модули этих чисел.
2. Чтобы перемножить два отрицательных числа, надо
а) перемножить модули этих чисел и поставить перед полученным числом знак « - »;
б) перемножить модули этих чисел.
3. Поставьте знак:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4. Чтобы разделить отрицательное число на отрицательное число, надо:
а) разделить модуль делимого на модуль делителя, поставить перед полученным числом знак « - »;
б) разделить модуль делимого на модуль делителя.
Ф.И._________________________________
Тест по теме «Умножение и деление положительных и отрицательных чисел»
-
Чтобы перемножить два числа с разными знаками, надо:
а) перемножить модули этих чисел и поставить перед полученным числом знак « - »;
б) перемножить модули этих чисел.
2. Чтобы перемножить два отрицательных числа, надо
а) перемножить модули этих чисел и поставить перед полученным числом знак « - »;
б) перемножить модули этих чисел.
3. Поставьте знак:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4. Чтобы разделить отрицательное число на отрицательное число, надо:
а) разделить модуль делимого на модуль делителя, поставить перед полученным числом знак « - »;
б) разделить модуль делимого на модуль делителя.
5. При делении чисел с разными знаками, надо:
а) разделить модуль делимого на модуль делителя, поставить перед полученным числом знак « - »;
б) разделить модуль делимого на модуль делителя.
6. Найдите значения выражений:
а) ![]() в)
в) ![]() д)
д) ![]() ж)
ж) ![]()
б) ![]() г)
г) ![]() е)
е)![]() з)
з) ![]()
5. При делении чисел с разными знаками, надо:
а) разделить модуль делимого на модуль делителя, поставить перед полученным числом знак « - »;
б) разделить модуль делимого на модуль делителя.
6. Найдите значения выражений:
а) ![]() в)
в) ![]() д)
д) ![]() ж)
ж) ![]()
б) ![]() г)
г) ![]() е)
е)![]() з)
з) ![]()
5. При делении чисел с разными знаками, надо:
а) разделить модуль делимого на модуль делителя, поставить перед полученным числом знак « - »;
б) разделить модуль делимого на модуль делителя.
6. Найдите значения выражений:
а) ![]() в)
в) ![]() д)
д) ![]() ж)
ж) ![]()
б) ![]() г)
г) ![]() е)
е)![]() з)
з) ![]()
Ф.И._________________________________
Тест по теме «Рациональные числа и свойства действий над ними»
-
Какое число называется рациональным?
а) число, которое можно записать в виде отношения ![]() , где а – целое число; п – натуральное;
, где а – целое число; п – натуральное;
б) число, которое можно записать в виде отношения ![]() , где а – целое число; п – натуральное.
, где а – целое число; п – натуральное.
2. Любое целое число а можно записать в виде ![]() , а значит оно является:
, а значит оно является:
а) натуральным; б) рациональным.
3. Верно ли, что любое рациональное число можно записать либо в виде десятичной дроби, либо в виде периодической? а) да; б) нет.
4. Сложение рациональных чисел обладает свойствами:
а) сочетательным, переместительным, распределительным;
б) сочетательным, переместительным.
Ф.И._________________________________
Тест по теме «Рациональные числа и свойства действий над ними»
-
Какое число называется рациональным?
а) число, которое можно записать в виде отношения ![]() , где а – целое число; п – натуральное;
, где а – целое число; п – натуральное;
б) число, которое можно записать в виде отношения ![]() , где а – целое число; п – натуральное.
, где а – целое число; п – натуральное.
2. Любое целое число а можно записать в виде ![]() , а значит оно является:
, а значит оно является:
а) натуральным; б) рациональным.
3. Верно ли, что любое рациональное число можно записать либо в виде десятичной дроби, либо в виде периодической? а) да; б) нет.
4. Сложение рациональных чисел обладает свойствами:
а) сочетательным, переместительным, распределительным;
б) сочетательным, переместительным.
Ф.И._________________________________
Тест по теме «Рациональные числа и свойства действий над ними»
-
Какое число называется рациональным?
а) число, которое можно записать в виде отношения ![]() , где а – целое число; п – натуральное;
, где а – целое число; п – натуральное;
б) число, которое можно записать в виде отношения ![]() , где а – целое число; п – натуральное.
, где а – целое число; п – натуральное.
2. Любое целое число а можно записать в виде ![]() , а значит оно является:
, а значит оно является:
а) натуральным; б) рациональным.
3. Верно ли, что любое рациональное число можно записать либо в виде десятичной дроби, либо в виде периодической? а) да; б) нет.
4. Сложение рациональных чисел обладает свойствами:
а) сочетательным, переместительным, распределительным относительно сложения;
б) сочетательным, переместительным.
5. Запишите свойства сложения рациональных чисел (все вам известные).
________________________________________________________________________________
________________________________________________________________________________
6. Умножение рациональных чисел обладает свойствами:
а) сочетательным, переместительным, распределительным относительно сложения;
б) сочетательным, переместительным.
7. Запишите свойства умножения рациональных чисел (все вам известные).
________________________________________________________________________________
________________________________________________________________________________
8. Произведение может быть равно нулю лишь в том случае, когда:
а) обязательно два множителя равны нулю;
б) хотя бы один из множителей равен нулю.
9. Выразите в виде десятичной или периодической дроби числа:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
5. Запишите свойства сложения рациональных чисел (все вам известные).
________________________________________________________________________________
________________________________________________________________________________
6. Умножение рациональных чисел обладает свойствами:
а) сочетательным, переместительным, распределительным относительно сложения;
б) сочетательным, переместительным.
7. Запишите свойства умножения рациональных чисел (все вам известные).
________________________________________________________________________________
________________________________________________________________________________
8. Произведение может быть равно нулю лишь в том случае, когда:
а) обязательно два множителя равны нулю;
б) хотя бы один из множителей равен нулю.
9. Выразите в виде десятичной или периодической дроби числа:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
5. Запишите свойства сложения рациональных чисел (все вам известные).
________________________________________________________________________________
________________________________________________________________________________
6. Умножение рациональных чисел обладает свойствами:
а) сочетательным, переместительным, распределительным относительно сложения;
б) сочетательным, переместительным.
7. Запишите свойства умножения рациональных чисел (все вам известные).
________________________________________________________________________________
________________________________________________________________________________
8. Произведение может быть равно нулю лишь в том случае, когда:
а) обязательно два множителя равны нулю;
б) хотя бы один из множителей равен нулю.
9. Выразите в виде десятичной или периодической дроби числа:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Ф.И._________________________________
Тест по теме «Раскрытие скобок. Коэффициент. Подобные слагаемые»
-
Если перед скобками стоит знак «+», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
-
Если перед скобками стоит знак «-», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
3. Если выражение является произведением числа и одной или нескольких букв, то это число называют:
а) подобным слагаемым;
б) коэффициентом.
Ф.И._________________________________
Тест по теме «Раскрытие скобок. Коэффициент. Подобные слагаемые»
-
Если перед скобками стоит знак «+», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
-
Если перед скобками стоит знак «-», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
3. Если выражение является произведением числа и одной или нескольких букв, то это число называют:
а) подобным слагаемым;
б) коэффициентом.
Ф.И._________________________________
Тест по теме «Раскрытие скобок. Коэффициент. Подобные слагаемые»
-
Если перед скобками стоит знак «+», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
-
Если перед скобками стоит знак «-», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
3. Если выражение является произведением числа и одной или нескольких букв, то это число называют:
а) подобным слагаемым;
б) коэффициентом.
4. Слагаемые имеющие одинаковую буквенную часть называются ________________________
5. Что нужно сделать, чтобы сложить (привести) подобные слагаемые _________________________________________________________________________________
6. Раскройте скобки и найдите значение выражения:
а) – 0,6 + (-4,4 + 3,8) = б) – 1,8 – (- 4,8 + 2,9) = в) ![]()
7. Приведите подобные слагаемые:
а) 3х + 15у – 2х – 20у + 7х = б) ![]()
8. Упростите выражение и подчеркните коэффициент:
а) -3 ∙ (-7с) ∙ 4р = б) -2,4m ∙ (-3.2) ∙ 5.5 = в) ![]()
4. Слагаемые имеющие одинаковую буквенную часть называются ________________________
5. Что нужно сделать, чтобы сложить (привести) подобные слагаемые _________________________________________________________________________________
6. Раскройте скобки и найдите значение выражения:
а) – 0,6 + (-4,4 + 3,8) = б) – 1,8 – (- 4,8 + 2,9) = в) ![]()
7. Приведите подобные слагаемые:
а) 3х + 15у – 2х – 20у + 7х = б) ![]()
8. Упростите выражение и подчеркните коэффициент:
а) -3 ∙ (-7с) ∙ 4р = б) -2,4m ∙ (-3.2) ∙ 5.5 = в) ![]()
4. Слагаемые имеющие одинаковую буквенную часть называются ________________________
5. Что нужно сделать, чтобы сложить (привести) подобные слагаемые _________________________________________________________________________________
6. Раскройте скобки и найдите значение выражения:
а) – 0,6 + (-4,4 + 3,8) = б) – 1,8 – (- 4,8 + 2,9) = в) ![]()
7. Приведите подобные слагаемые:
а) 3х + 15у – 2х – 20у + 7х = б) ![]()
8. Упростите выражение и подчеркните коэффициент:
а) -3 ∙ (-7с) ∙ 4р = б) -2,4m ∙ (-3.2) ∙ 5.5 = в) ![]()
Тест по теме «Решение уравнений» Ф.И._________________________________
I вариант
-
Корни уравнения не изменяются, если:
1)___________________________________________________________________________2)___________________________________________________________________________ ____________________________________________________________________________
2. Решите уравнение: а) 14 +5 х =4х + 3х; х =
б) 3а + 5 = 8а – 15; а =
в) 5(х + 1,2) = 12,5х; х =
г) ![]() у =
у =
Тест по теме «Решение уравнений» Ф.И._________________________________
II вариант
-
Корни уравнения не изменяются, если:
1)___________________________________________________________________________2)___________________________________________________________________________ ____________________________________________________________________________
2. Решите уравнение: а) 4х +12 = 3х + 8; х =
б) 3в – 35 - 2в = 6в; в =
в) 0,4(6х – 7) = 0,5(3х + 7); х =
г) ![]() у =
у =
Тест по теме «Решение уравнений» Ф.И._________________________________
I вариант
-
Корни уравнения не изменяются, если:
1)___________________________________________________________________________2)___________________________________________________________________________ ____________________________________________________________________________
2. Решите уравнение: а) 14 +5 х =4х + 3х; х =
б) 3а + 5 = 8а – 15; а =
в) 5(х + 1,2) = 12,5х; х =
г) ![]() у =
у =
Тест по теме «Решение уравнений» Ф.И._________________________________
II вариант
-
Корни уравнения не изменяются, если:
1)___________________________________________________________________________2)___________________________________________________________________________ ____________________________________________________________________________
2. Решите уравнение: а) 4х +12 = 3х + 8; х =
б) 3в – 35 - 2в = 6в; в =
в) 0,4(6х – 7) = 0,5(3х + 7); х =
г) ![]() у =
у =
Тест по теме «Перпендикулярные и параллельные прямые. Координатная плоскость »
1. Перпендикулярными прямыми называются:
а) две непересекающиеся прямые;
б) две прямые, образующие при пересечении прямые углы.
2. Параллельными прямыми называются:
а) две непересекающиеся прямые;
б) две прямые, образующие при пересечении прямые углы.
3. Если две прямые в плоскости перпендикулярны третьей прямой, то они:
а) перпендикулярны; б) параллельны.
4. Сколько прямых можно провести через каждую точку плоскости, не лежащую на данной прямой: а) одну; б) ни одной; в) множество.
5. Ось ординат – это: а) х; б) у.
6. Ось абсцисс – это: а) х; б) у.
Тест по теме «Перпендикулярные и параллельные прямые. Координатная плоскость »
1. Перпендикулярными прямыми называются:
а) две непересекающиеся прямые;
б) две прямые, образующие при пересечении прямые углы.
2. Параллельными прямыми называются:
а) две непересекающиеся прямые;
б) две прямые, образующие при пересечении прямые углы.
3. Если две прямые в плоскости перпендикулярны третьей прямой, то они:
а) перпендикулярны; б) параллельны.
4. Сколько прямых можно провести через каждую точку плоскости, не лежащую на данной прямой: а) одну; б) ни одной; в) множество.
5. Ось ординат – это: а) х; б) у.
6. Ось абсцисс – это: а) х; б) у.
Тест по теме «Перпендикулярные и параллельные прямые. Координатная плоскость »
1. Перпендикулярными прямыми называются:
а) две непересекающиеся прямые;
б) две прямые, образующие при пересечении прямые углы.
2. Параллельными прямыми называются:
а) две непересекающиеся прямые;
б) две прямые, образующие при пересечении прямые углы.
3. Если две прямые в плоскости перпендикулярны третьей прямой, то они:
а) перпендикулярны; б) параллельны.
4. Сколько прямых можно провести через каждую точку плоскости, не лежащую на данной прямой: а) одну; б) ни одной; в) множество.
5. Ось ординат – это: а) координатную прямую х; б) координатную прямую у.
6. Ось абсцисс – это: а) координатную прямую х; б) координатную прямую у.
7. Прямые х и у называют - …
8. Точка О – это…
9. Постройте в координатной плоскости точки К(-3;-2), L(-3;5), M(-4;0), N(0;2), P(4;-2), T(4;4).
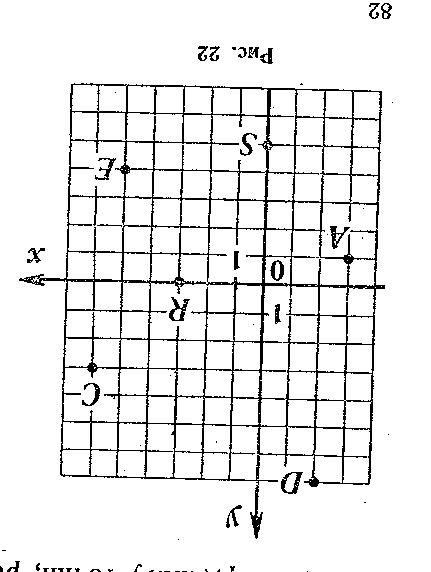
10. По рисунку определите координаты точек A, B, C, D, R, S.

7. Прямые х и у называют - …
8. Точка О – это…
9. Постройте в координатной плоскости точки К(-3;-2), L(-3;5), M(-4;0), N(0;2), P(4;-2), T(4;4).
10. По рисунку определите координаты точек A, B, C, D, R, S.

7. Прямые х и у называют - …
8. Точка О – это…
9. Постройте в координатной плоскости точки К(-3;-2), L(-3;5), M(-4;0), N(0;2), P(4;-2), T(4;4).
10. По рисунку определите координаты точек A, B, C, D, R, S.



Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
(0;0); (-1;1); (-3;1); (-2;2); (-3;3); (-4;6); (0;8); (2;5); (2;8); (6;0); (6;10); (3;9); (4;5); (3;0); (2;0); (1;-7); (3;-8); (0;-8); (0;0).
Название: «__________________»
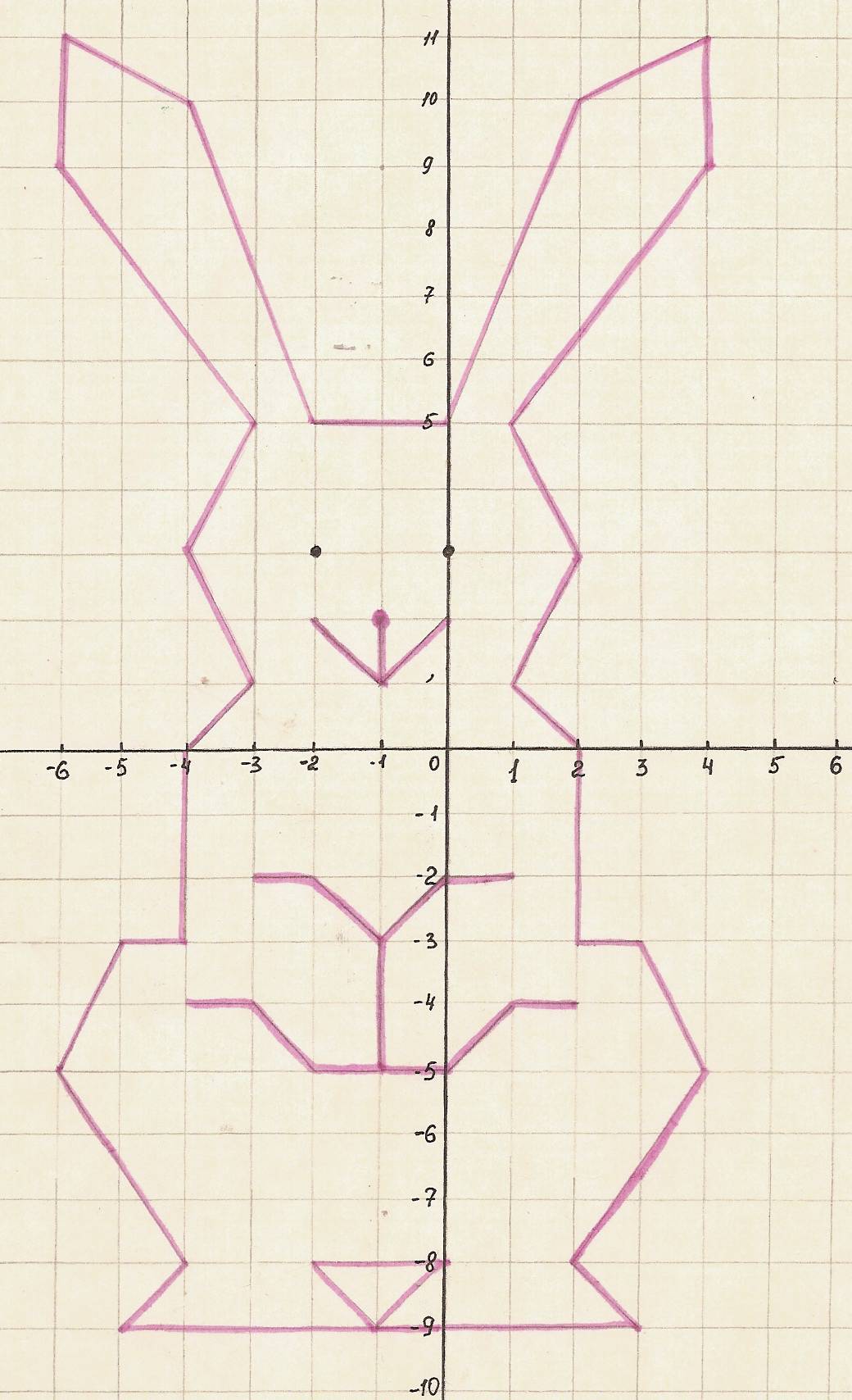
(-1;3); (-5;0); (-7;0); (-3;9); (-1;11); (1;11); (3;9); (7;0); (5;0); (1;3); (-1;3); (-2;1); (-2;-1); (-3;-2); (-2;-2); (-2;-8); (-1;-9); (1;-9); (2;-8); (2;-2); (3;-2); (2;-1); (2;1); (1;3).
(-2;-2); (-1;-3); (0;-2); (1;-3); (2;-2).
Название: «__________________»
(-1;3); (-5;0); (-7;0); (-3;9); (-1;11); (1;11); (3;9); (7;0); (5;0); (1;3); (-1;3); (-2;1); (-2;-1); (-3;-2); (-2;-2); (-2;-8); (-1;-9); (1;-9); (2;-8); (2;-2); (3;-2); (2;-1); (2;1); (1;3).
(-2;-2); (-1;-3); (0;-2); (1;-3); (2;-2).
Название: «__________________»
(-1;3); (-5;0); (-7;0); (-3;9); (-1;11); (1;11); (3;9); (7;0); (5;0); (1;3); (-1;3); (-2;1); (-2;-1); (-3;-2); (-2;-2); (-2;-8); (-1;-9); (1;-9); (2;-8); (2;-2); (3;-2); (2;-1); (2;1); (1;3).
(-2;-2); (-1;-3); (0;-2); (1;-3); (2;-2).
Название: «__________________»
(-1;3); (-5;0); (-7;0); (-3;9); (-1;11); (1;11); (3;9); (7;0); (5;0); (1;3); (-1;3); (-2;1); (-2;-1); (-3;-2); (-2;-2); (-2;-8); (-1;-9); (1;-9); (2;-8); (2;-2); (3;-2); (2;-1); (2;1); (1;3).
(-2;-2); (-1;-3); (0;-2); (1;-3); (2;-2).
Название: «__________________»
(-1;3); (-5;0); (-7;0); (-3;9); (-1;11); (1;11); (3;9); (7;0); (5;0); (1;3); (-1;3); (-2;1); (-2;-1); (-3;-2); (-2;-2); (-2;-8); (-1;-9); (1;-9); (2;-8); (2;-2); (3;-2); (2;-1); (2;1); (1;3).
(-2;-2); (-1;-3); (0;-2); (1;-3); (2;-2).
Название: «__________________»
(-1;3); (-5;0); (-7;0); (-3;9); (-1;11); (1;11); (3;9); (7;0); (5;0); (1;3); (-1;3); (-2;1); (-2;-1); (-3;-2); (-2;-2); (-2;-8); (-1;-9); (1;-9); (2;-8); (2;-2); (3;-2); (2;-1); (2;1); (1;3).
(-2;-2); (-1;-3); (0;-2); (1;-3); (2;-2).
Здесь представлены материалы теста на тему «Сокращение дробей. Сравнение, сложение и вычитание дробей с разными знаменателями», которые могут быть просмотрены в онлайн режиме или же их можно бесплатно скачать. Предмет теста: Математика (все классы). Также здесь Вы найдете подборку тестов на схожие темы, что поможет в еще лучшей подготовке к тестированию.

