Слайд 13.1 Сила тока. Плотность тока. Уравнение неразрывности
ЛЕКЦИЯ 3. ЭЛЕКТРИЧЕСКИЙ ТОК
Слайд 2Электрический ток. Носители электрического тока
Электродинамика – раздел учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов. Электрическим током называется упорядоченное движение электрических зарядов. За направление тока принимают направление движения положительных зарядов. Носителями тока в проводящей среде являются электроны (в металлах), ионы (в электролитах), либо другие частицы. Токи подразделяются на: конвекционные (сопровождающиеся переносом вещества); токи проводимости (не сопровождающиеся переносом вещества)
Слайд 3Электрический ток
В общем случае носители тока участвуют в хаотическом (тепловом) движении внутри проводника так, что через любую поверхность S в среднем проводит одинаковое число носителей. При наложении внешнего электрического поля на хаотические движение накладывается упорядоченное движение носителей с некоторой постоянной скоростью, и через поверхность S течет ток.
Слайд 4Сила тока
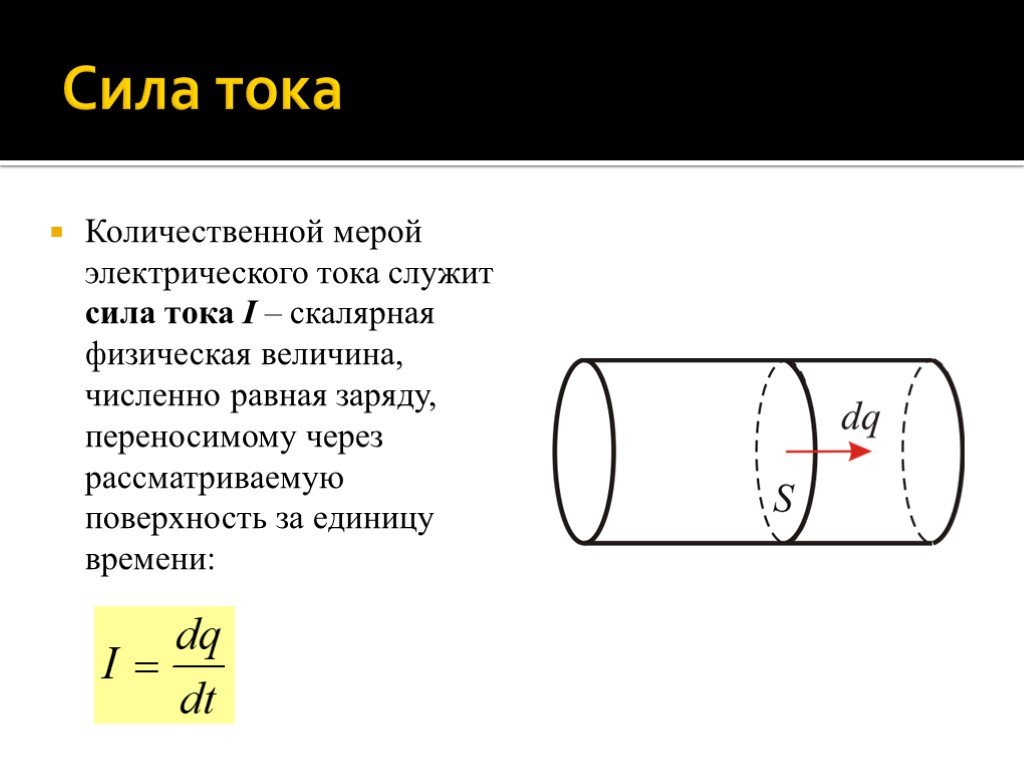
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, численно равная заряду, переносимому через рассматриваемую поверхность за единицу времени:
Слайд 5Постоянный электрический ток
Электрический ток называется постоянным, если сила тока и его направление не изменяются с течением времени: Здесь q – заряд, переносимый через рассматриваемую поверхность за время .
Слайд 6Единица силы тока
Единицей силы тока является ампер (А) Один ампер (1 А) – это такая сила тока, протекающего по двум прямолинейным параллельным бесконечно длинным тонким проводникам, расположенным в вакууме на расстоянии 1 м друг от друга, при которой данные проводники взаимодействуют с силой 0,2 мкН в расчете на один метр длины каждого проводника. Данная сила взаимодействия имеет магнитную природу.
Слайд 7Плотность тока
Электрический ток может быть распределен по поверхности, через которую он протекает, неравномерно. Поэтому для более детальной характеристики тока вводят вектор плотности тока j. Плотность тока – вектор, модуль которого равен отношению силы тока dI через элементарную площадку, расположенную в данной точке перпендикулярно направлению движения носителей, к ее площади:
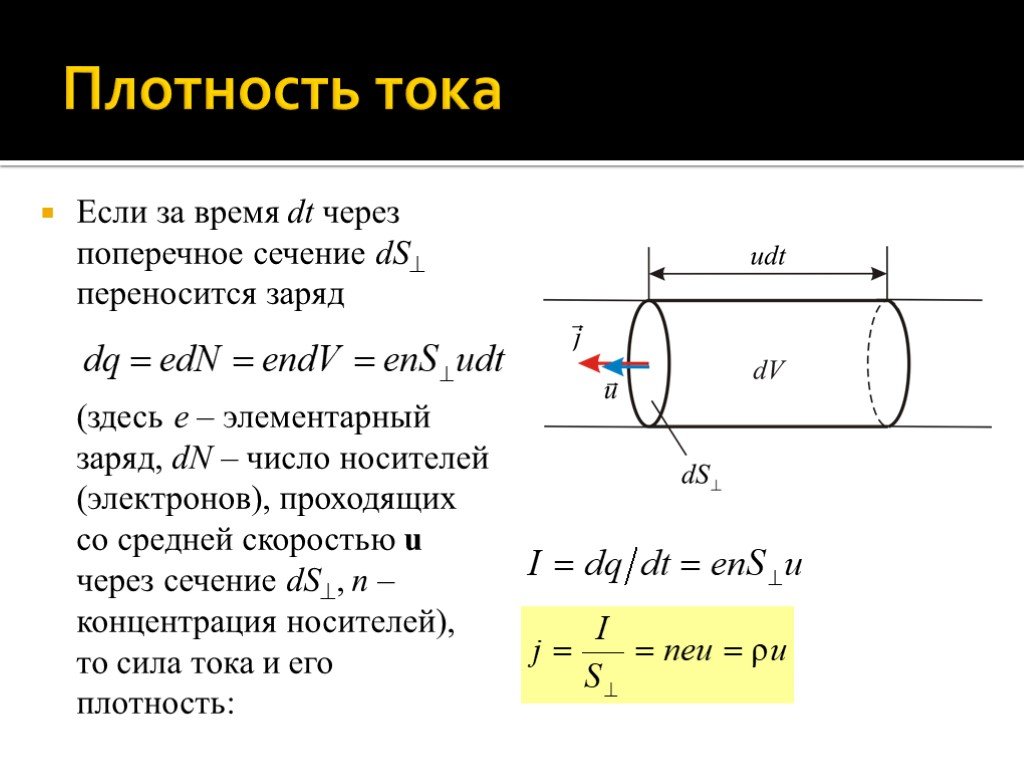
Слайд 8Если за время dt через поперечное сечение dS переносится заряд (здесь e – элементарный заряд, dN – число носителей (электронов), проходящих со средней скоростью u через сечение dS, n – концентрация носителей), то сила тока и его плотность:
Слайд 9За направление вектора j принимают направление вектора скорости u упорядоченного движения положительных носителей. Если носителями являются заряды разных знаков с объемными плотностями + и – и скоростями их упорядоченного движения u+ и u– соответственно, то вектор плотности тока j определяется следующим образом: В проводниках: j = –u–
Слайд 10Плотность тока и сила тока
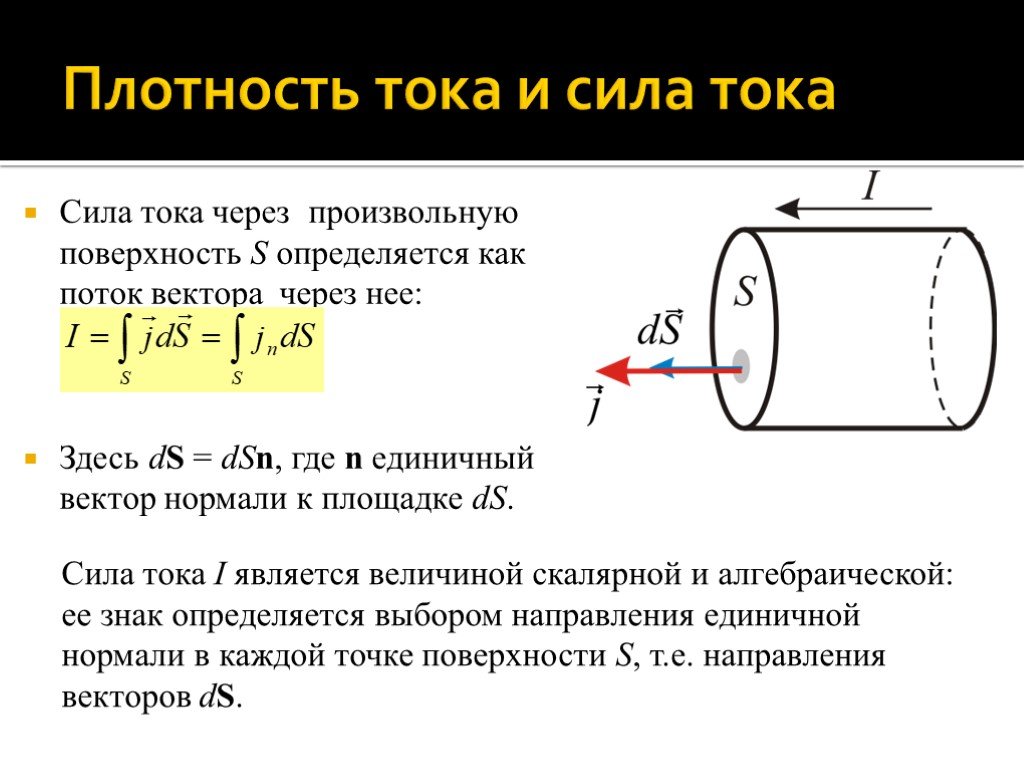
Сила тока через произвольную поверхность S определяется как поток вектора через нее: Здесь dS = dSn, где n единичный вектор нормали к площадке dS.
Сила тока I является величиной скалярной и алгебраической: ее знак определяется выбором направления единичной нормали в каждой точке поверхности S, т.е. направления векторов dS.
Слайд 11Линии тока
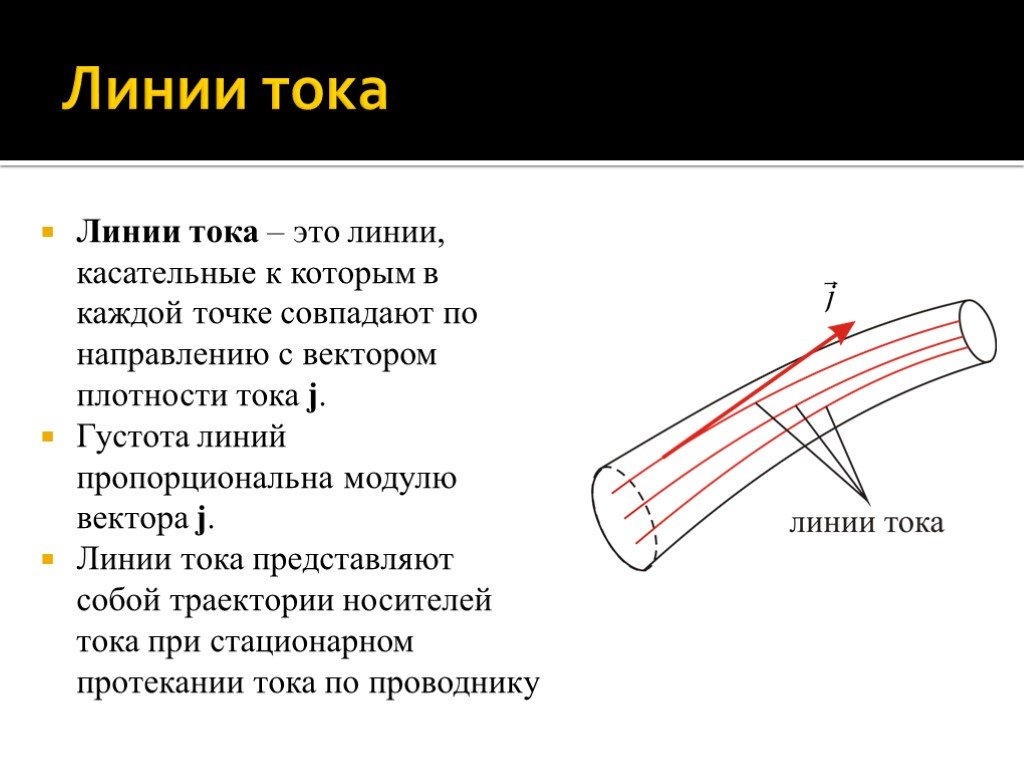
Линии тока – это линии, касательные к которым в каждой точке совпадают по направлению с вектором плотности тока j. Густота линий пропорциональна модулю вектора j. Линии тока представляют собой траектории носителей тока при стационарном протекании тока по проводнику
Слайд 12Уравнение непрерывности
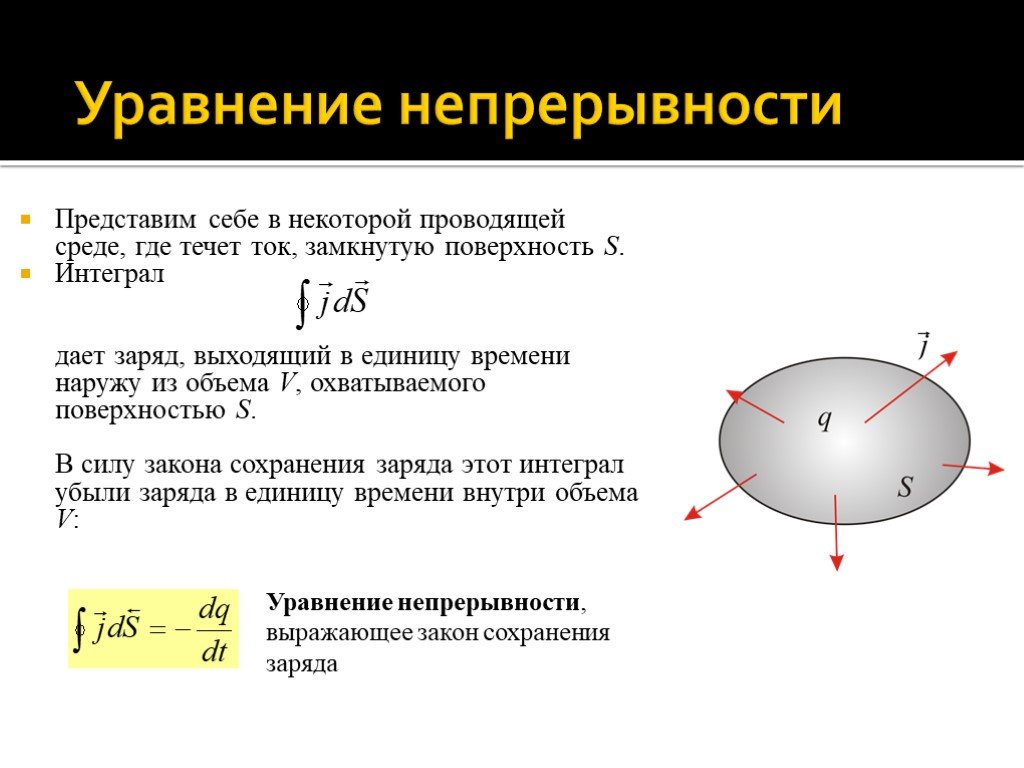
Представим себе в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Интеграл дает заряд, выходящий в единицу времени наружу из объема V, охватываемого поверхностью S. В силу закона сохранения заряда этот интеграл убыли заряда в единицу времени внутри объема V:
Уравнение непрерывности, выражающее закон сохранения заряда
Слайд 13Уравнение непрерывности в случае стационарного (постоянного) тока
В случае стационарного (постоянного) тока распределение зарядов в пространстве должно оставаться неизменным, т.е. в правой части уравнения непрерывности dq/dt = 0. Следовательно, для постоянного тока Иначе говоря, линии вектора j нигде не начинаются и нигде не заканчиваются. Говорят, что в случае постоянного тока поле вектора j не имеет источников.
Слайд 14Уравнение непрерывности в дифференциальной форме
Преобразуем последние два уравнения к дифференциальной форме. Как было сделано ранее для потока вектора E, получим, что дивергенция вектора j в некоторой точке равна убыли плотности заряда в единицу времени в той же точке:
Для постоянного тока: div j = j = 0, т.е. поле вектора j не имеет источников и стоков.
Слайд 153.2 Закон Ома для однородного участка цепи
Слайд 16Закон Ома для однородного участка цепи
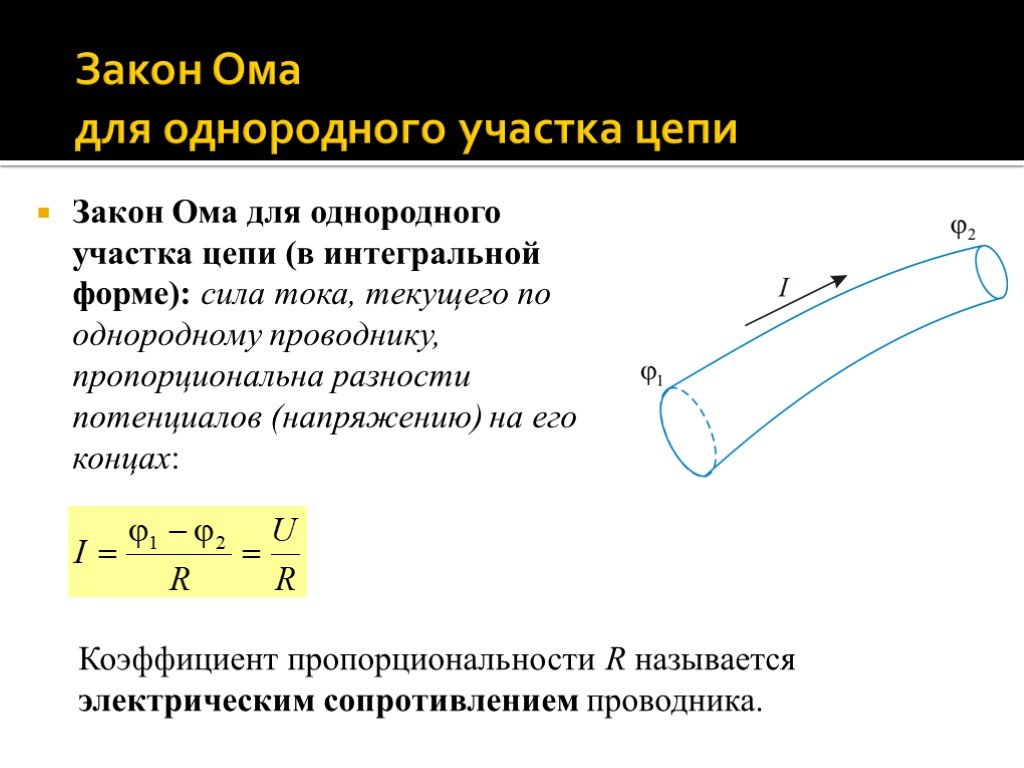
Закон Ома для однородного участка цепи (в интегральной форме): сила тока, текущего по однородному проводнику, пропорциональна разности потенциалов (напряжению) на его концах:
Коэффициент пропорциональности R называется электрическим сопротивлением проводника.
Слайд 17Электрическое сопротивление
Единица электрического сопротивления – ом (Ом). 1 Ом – сопротивление такого проводника, при котором при напряжении 1 В течет постоянный ток силой 1 А. Величина G = R-1 называется электрической проводимостью проводника. Ее единица измерения – сименс (См). Сопротивление R проводника зависит от его размеров и формы, а также из материала, из которого этот проводник изготовлен.
Слайд 18Например, для однородного линейного проводника длиной l и площадью поперечного сечения S сопротивление рассчитывается по формуле: Здесь – удельное электрическое сопротивление – величина, характеризующая материал проводника. Единица удельного электрического сопротивления – ом-метр (Омм). Для наиболее хороших проводников при комнатной температуре составляет ~ 10-8 Омм.
Слайд 19Закон Ома в дифференциальной (локальной) форме
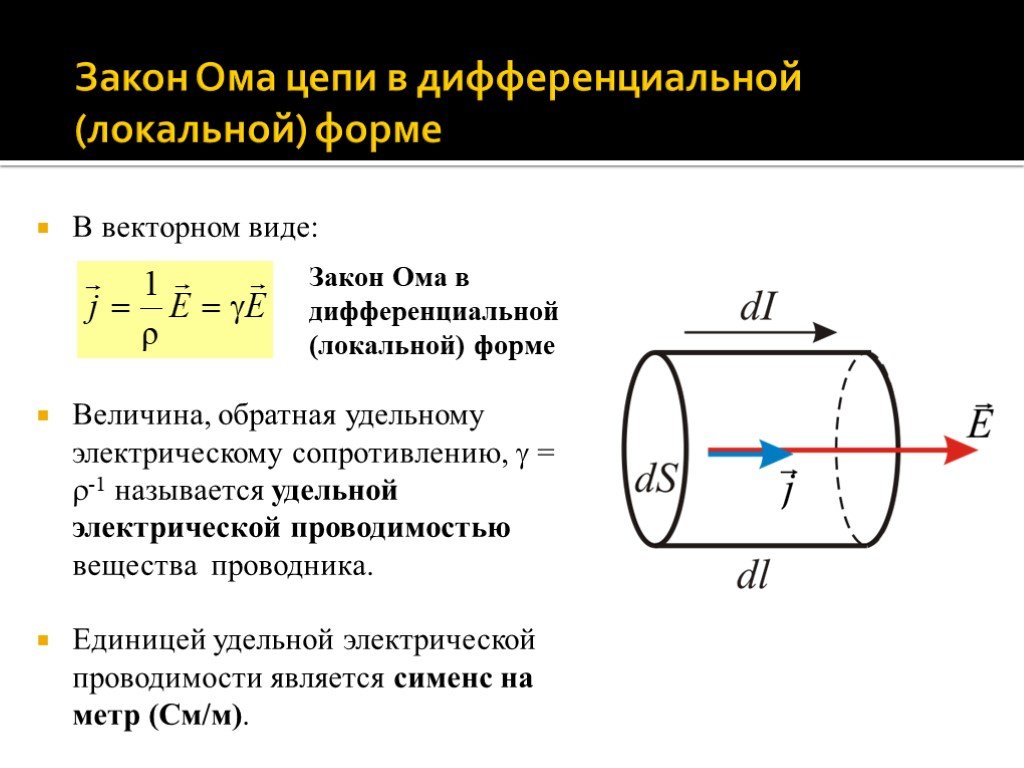
Найдем связь между плотностью тока j и полем E в одной и той же точке однородного изотропного проводника (в котором jE). Мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными j и E и поперечным сечением dS и длиной dl. Тогда
Слайд 20Закон Ома цепи в дифференциальной (локальной) форме
В векторном виде: Величина, обратная удельному электрическому сопротивлению, = -1 называется удельной электрической проводимостью вещества проводника. Единицей удельной электрической проводимости является сименс на метр (См/м).
Слайд 21Зависимость сопротивления проводника от температуры
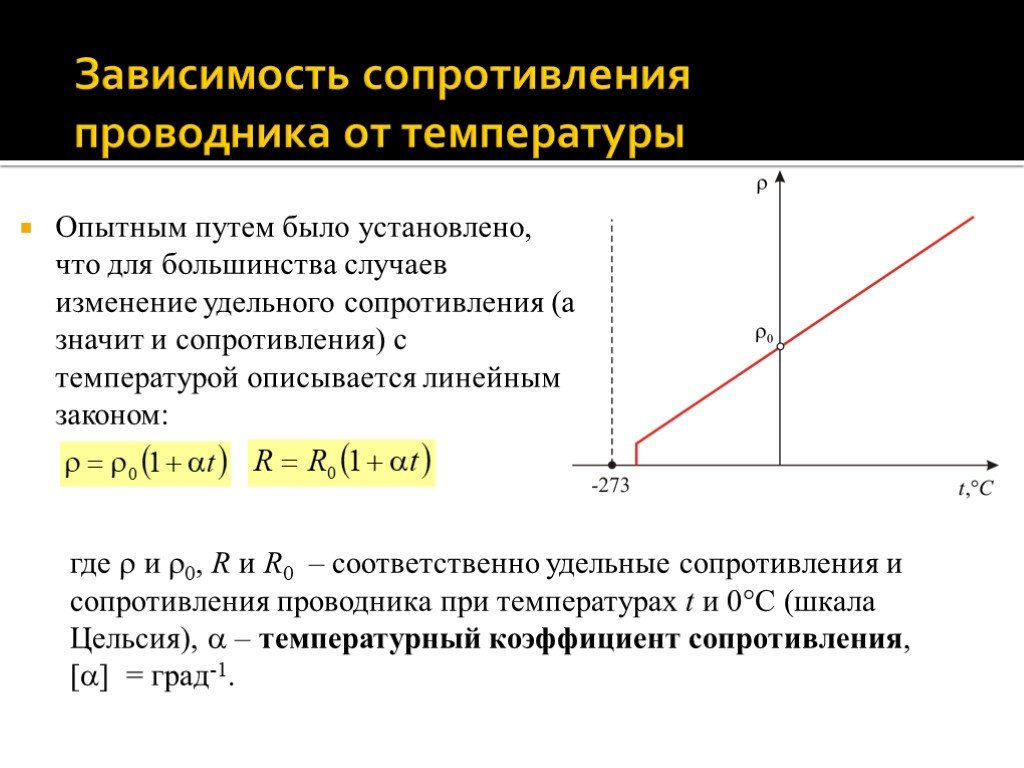
Опытным путем было установлено, что для большинства случаев изменение удельного сопротивления (а значит и сопротивления) с температурой описывается линейным законом:
где и 0, R и R0 – соответственно удельные сопротивления и сопротивления проводника при температурах t и 0С (шкала Цельсия), – температурный коэффициент сопротивления, [] = град-1.
Слайд 22Заряд внутри проводника с током
Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, согласно уравнению непрерывности, закону Ома в локальной форме и теореме Гаусса для вектора E: Избыточный заряд может появиться только на поверхности проводника, в местах соприкосновения с другими проводниками, где проводник имеет неоднородности.
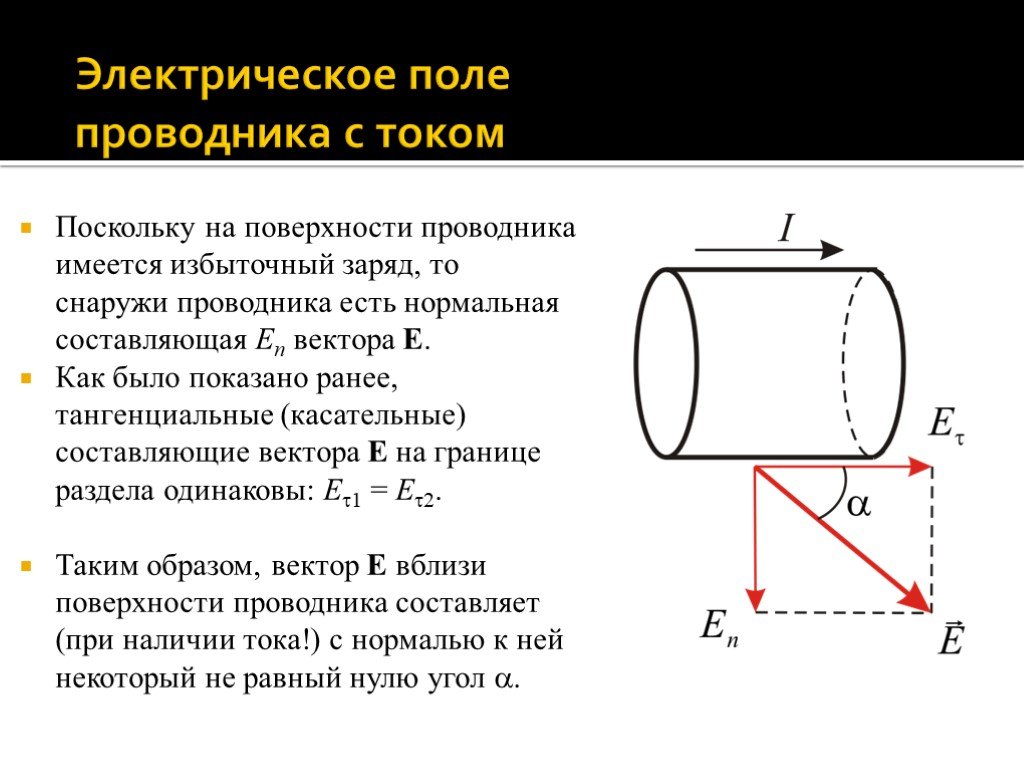
Слайд 23Электрическое поле проводника с током
Поскольку на поверхности проводника имеется избыточный заряд, то снаружи проводника есть нормальная составляющая En вектора E. Как было показано ранее, тангенциальные (касательные) составляющие вектора E на границе раздела одинаковы: E1 = E2. Таким образом, вектор E вблизи поверхности проводника составляет (при наличии тока!) с нормалью к ней некоторый не равный нулю угол .
Слайд 24Поле движущихся зарядов
Если токи стационарны, то распределение электрических зарядов в проводнике не меняется с течением времени: в каждой точке на место уходящих зарядов поступают новые. Эти заряды создают такое же кулоновское поле, что и неподвижные заряды той же конфигурации. Поэтому электрическое поле стационарных токов является потенциальным. Однако, это поле существенно отливается от электростатического: внутри проводника напряженность E электростатического поля равна нулю.
Слайд 253.1 Обобщенный закон Ома
Слайд 26Условия возникновения и существования тока
Для возникновения и осуществления электрического тока необходимы следующие условия: наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно; наличие электрического поля, энергия которого должна каким-то образом восполняться. Если в цепи действуют только силы электрического поля, то перемещение носителей происходит таким образом, что положительные носители перемещались бы из точек с большим потенциалом в точки с меньшим потенциалом, потенциалы точек, что привело бы к выравниванию потенциалов, исчезновению электрического поля и прекращению протекания электрического тока.

Слайд 27Чтобы этого не произошло, в цепь необходимо включить устройство, которое бы выполняло следующую функцию: направляло положительные носители тока в точки с большим потенциалом, а отрицательные – в точки с меньшим потенциалом, т.е. действовало бы против сил электрических (кулоновских) сил и поддерживало бы разность потенциалов между двумя любыми точками цепи. Такие устройства называются источниками тока.

Слайд 28Сторонние силы
Силы не электростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними силами. Природа сторонних сил: в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе – за счет механической энергии вращения ротора генератора; в солнечных батареях – за счет энергии света (фотонов) и т.п. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электрического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет электрический ток.
Слайд 29Напряженность поля сторонних сил
Количественная характеристика сторонних сил – поле сторонних сил и его напряженность Eстор, определяемая сторонней силой, действующей на единичный положительный заряд: Участок цепи, на котором действуют сторонние силы, называется неоднородным.
Слайд 30Обобщенный закон Ома в локальной форме
Если под действием электрического поля E возникает ток плотности j = E, то очевидно, что под совместным действием поля кулоновских сил E и поля сторонних сил Eстор, плотность тока: Это уравнение обобщает закон Ома на случай неоднородных участков проводника. Оно выражает обобщенный закон Ома в локальной форме.
Слайд 31Закон Ома для неоднородного участка цепи
Пусть электрический ток течет вдоль тонких проводов. В этом случае направление тока совпадает с направлением оси провода и j = const во всех точках его сечения. Преобразуем уравнение обобщенного закона Ома: разделим его на , умножим скалярно на элемент dl, взятый по направлению от сечения 1 к сечению 2 и проинтегрируем по длине провода от точки 1 до точки 2:
Слайд 32Рассмотрим правую часть уравнения. Учтем, что = 1/, jdl = jldl = I/S. Тогда правая часть последнего уравнения примет вид: Здесь R – сопротивление провода между точками 1 и 2.
Слайд 33Теперь рассмотрим левую часть уравнения. Первое слагаемое уравнения – это разность потенциалов между точками 1 и 2: Второе слагаемое представляет собой электродвижущую силу (ЭДС), действующую на участке 1-2:
Слайд 34Электродвижущая сила на участке цепи – скалярная физическая величина, численно равная работе сторонних сил при перемещении единичного положительного заряда вдоль этого участка: Эта работа совершается за счет энергии, затрачиваемой в источнике тока, поэтому ЭДС можно назвать электродвижущей силой источника тока, включенного в цепь. ЭДС, как и потенциал, измеряется в вольтах.
Слайд 35Таким образом, после указанных преобразований, получим закон Ома для неоднородного участка цепи:
Слайд 36Напряжение на участке цепи
Напряжением U на участке 1-2 называется скалярная физическая величина, численно равная суммарной работе, совершаемой электростатическими и сторонними силами по перемещению единичного положительного заряда на данном участке цепи:
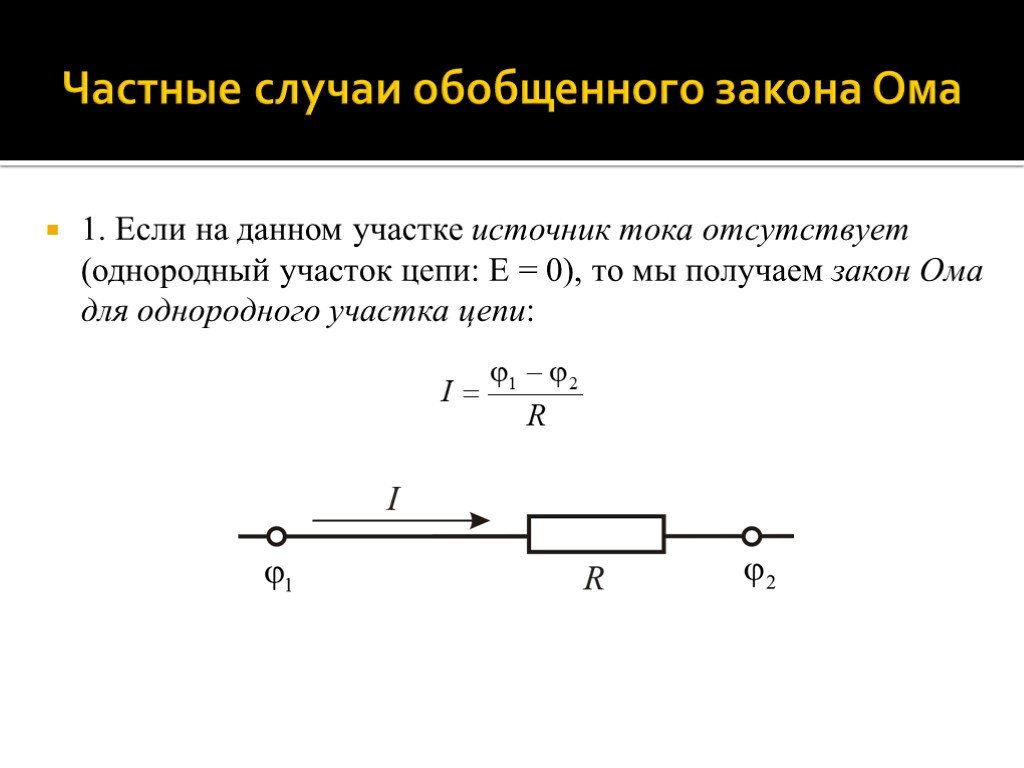
Слайд 37Частные случаи обобщенного закона Ома
1. Если на данном участке источник тока отсутствует (однородный участок цепи: = 0), то мы получаем закон Ома для однородного участка цепи:
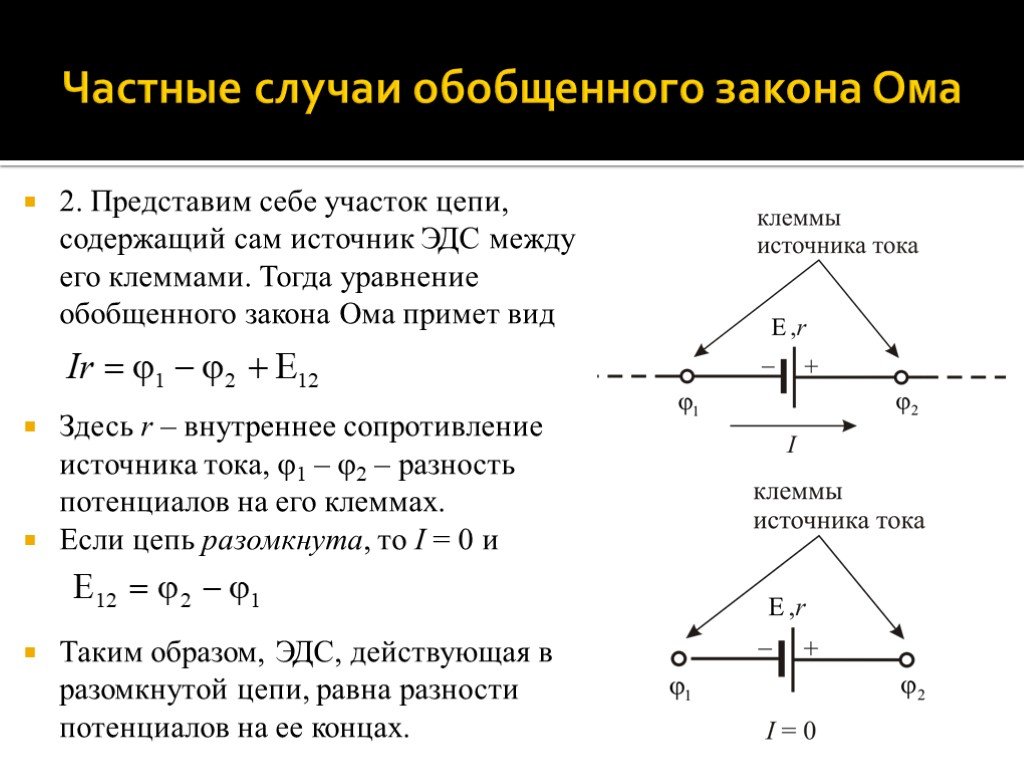
Слайд 382. Представим себе участок цепи, содержащий сам источник ЭДС между его клеммами. Тогда уравнение обобщенного закона Ома примет вид Здесь r – внутреннее сопротивление источника тока, 1 – 2 – разность потенциалов на его клеммах. Если цепь разомкнута, то I = 0 и Таким образом, ЭДС, действующая в разомкнутой цепи, равна разности потенциалов на ее концах.
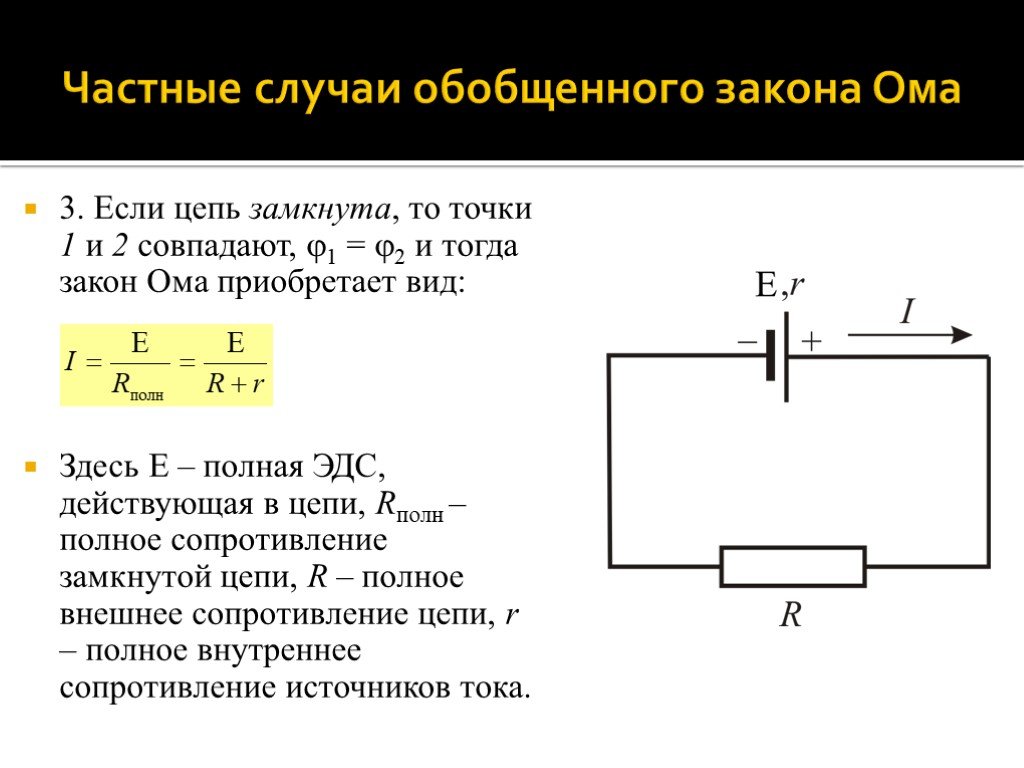
Слайд 393. Если цепь замкнута, то точки 1 и 2 совпадают, 1 = 2 и тогда закон Ома приобретает вид: Здесь – полная ЭДС, действующая в цепи, Rполн – полное сопротивление замкнутой цепи, R – полное внешнее сопротивление цепи, r – полное внутреннее сопротивление источников тока.
Слайд 40Поле сторонних сил
ЭДС, действующая в замкнутой цепи, численно равна работе сторонних сил при перемещении единичного положительного заряда по цепи: Следовательно, циркуляция вектора напряженности сторонних сил по замкнутому контуру не равна нулю. Поэтому поле сторонних сил непотенциально.
Слайд 414. Если цепь замкнута и отсутствует внешнее сопротивление R, то в такой цепи протекает ток короткого замыкания:
Слайд 423.4 Разветвленные электрические цепи. Правила Кирхгофа
Слайд 43Первое правило Кирхгофа
Расчет разветвленных цепей, например, нахождение токов в ее отдельных ветвях, значительно упрощается, если воспользоваться двумя правилами Кирхгофа.
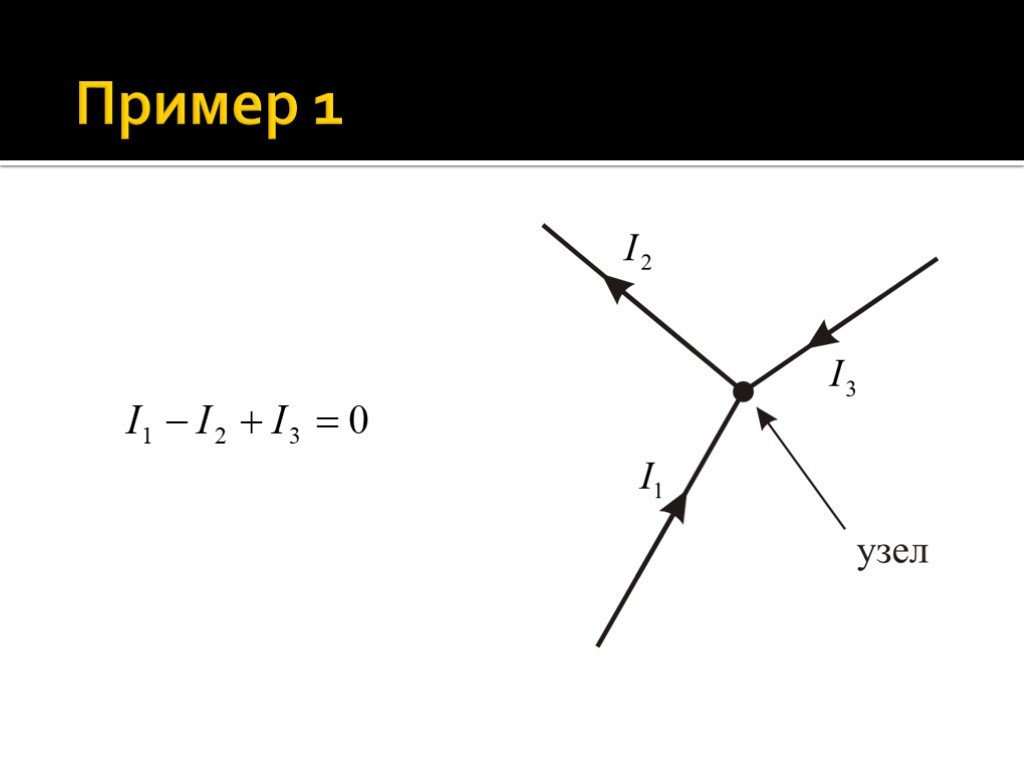
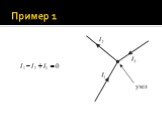
Слайд 44Первое правило Кирхгофа, относится к узлам цепи, т.е. к точкам ее разветвления: алгебраическая сумма токов, сходящихся в узле, равна нулю: При этом токи, идущие к узлу имеют положительный знак, исходящие из узла – отрицательный. Уравнение первого правила Кирхгофа является следствием условия стационарности.
Слайд 46Второе правило Кирхгофа
Второе правило Кирхгофа – оно относится к любому выделенному в разветвленной цепи замкнутому контуру: алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивления равна алгебраической сумме ЭДС, действующих в этом контуре: Второе правило Кирхгофа является следствием закон Ома для неоднородного участка цепи.
Слайд 47Алгоритм использования правил Кирхгофа
1. Произвольно обозначить стрелками положительные направления токов. Если при вычисления ток окажется отрицательным, то его направление противоположно выбранному. 2. Произвольно выбрать замкнутый контур и направление его обхода. 2.1 Если направление тока Ii в уравнении 2-го правила Кирхгофа совпадает с направлением обхода, то соответствующее слагаемое Ii Ri , берется со знаком «+», если противоположно – со знаком «–». 2.2 Если какая-то ЭДС i повышает потенциал в направлении обхода, то она берется со знаком «+», если понижает – со знаком «–».

Слайд 48Количество уравнений
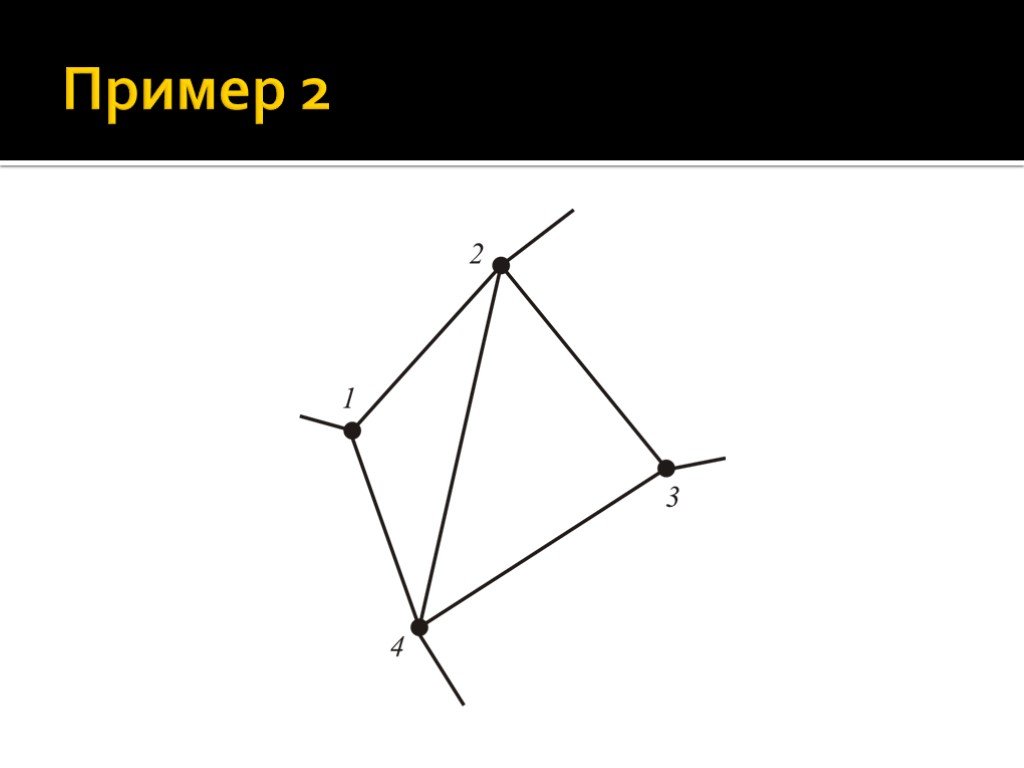
Уравнений необходимо составить столько, чтобы их количество было равно числу неизвестных величин (обычно, токов). Если разветвленная цепь содержит N узлов, то независимые уравнения 1-го правила Кирхгофа можно составить только для N – 1 узлов. Если в разветвленной цепи можно выделить несколько замкнутых контуров, то независимые уравнения 2-го правила Кирхгофа можно составить только для тех контуров, которые не получаются в результате наложения уже рассмотренных.
Слайд 50Пример 3. Шунт
Для измерения токов I, превышающих максимальный ток I0, на который рассчитан амперметр, имеющий внутреннее сопротивление R0, параллельно ему включают добавочное сопротивление Rш, называемое шунтом. Найдем его сопротивление по правилам Кирхгофа: Откуда
Слайд 51Пример 4. Добавочное сопротивление
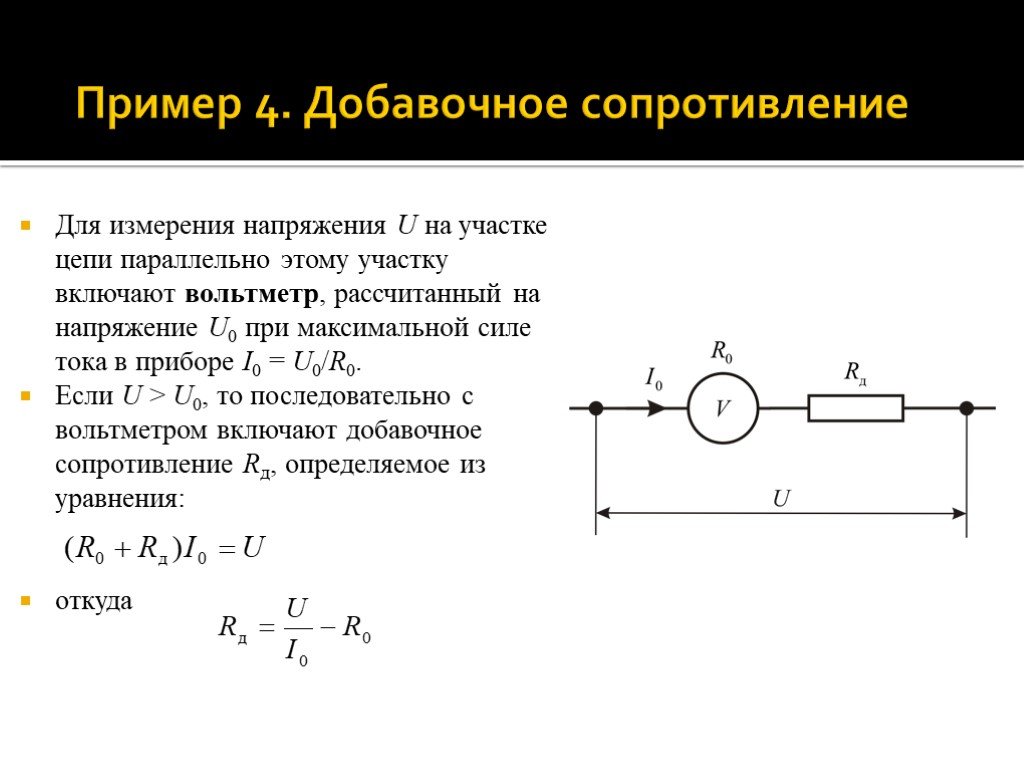
Для измерения напряжения U на участке цепи параллельно этому участку включают вольтметр, рассчитанный на напряжение U0 при максимальной силе тока в приборе I0 = U0/R0. Если U > U0, то последовательно с вольтметром включают добавочное сопротивление Rд, определяемое из уравнения: откуда
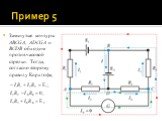
Слайд 52Пример 5
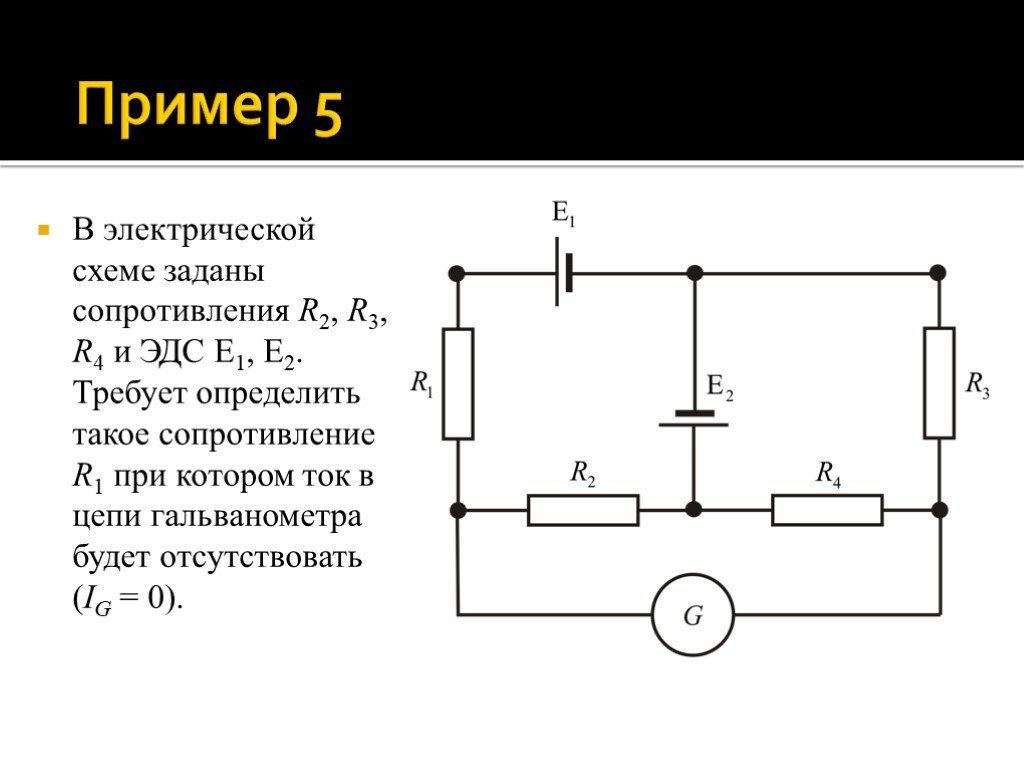
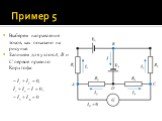
В электрической схеме заданы сопротивления R2, R3, R4 и ЭДС 1, 2. Требует определить такое сопротивление R1 при котором ток в цепи гальванометра будет отсутствовать (IG = 0).
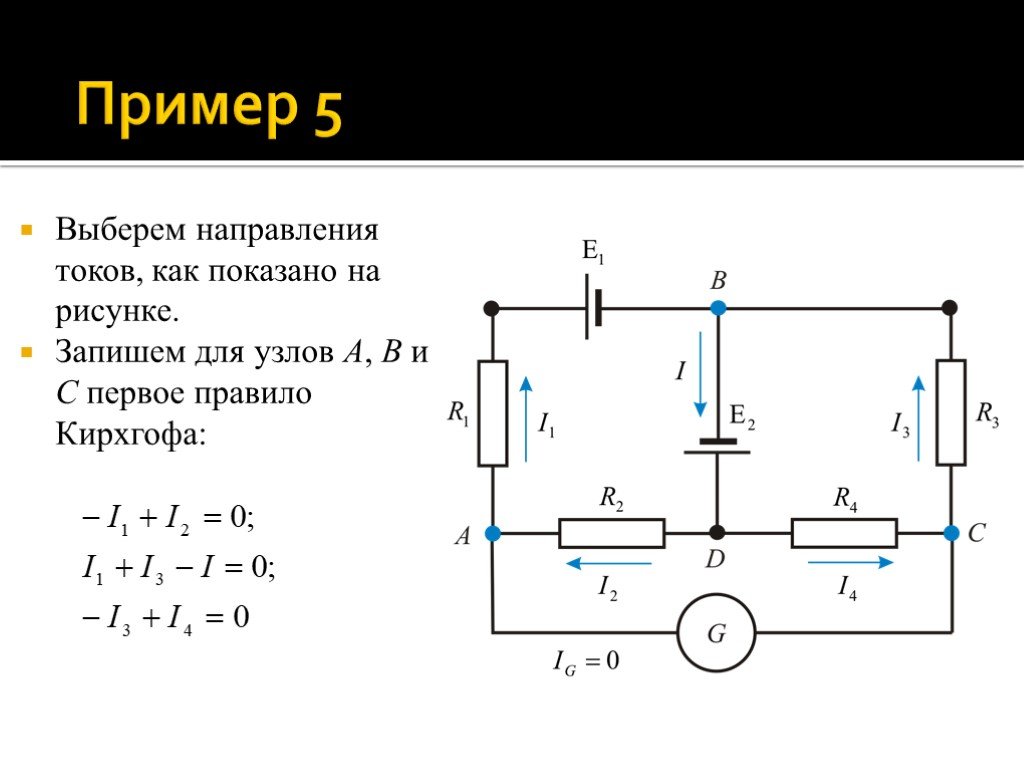
Слайд 53Выберем направления токов, как показано на рисунке. Запишем для узлов A, B и C первое правило Кирхгофа:
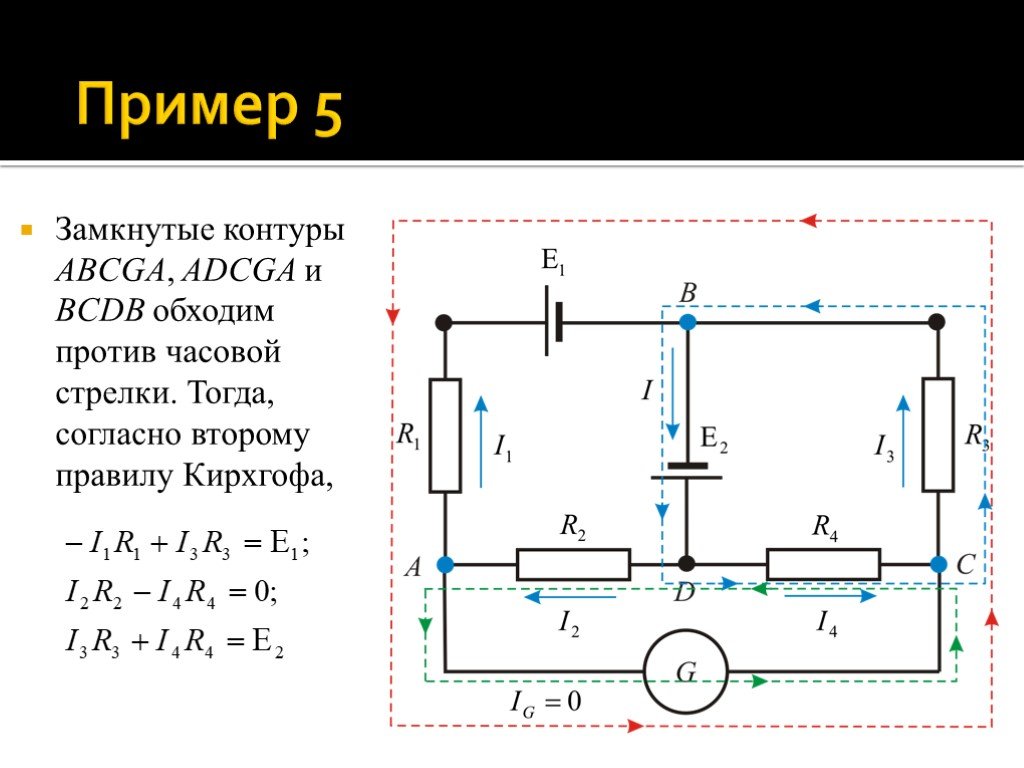
Слайд 54Замкнутые контуры ABCGA, ADCGA и BCDB обходим против часовой стрелки. Тогда, согласно второму правилу Кирхгофа,
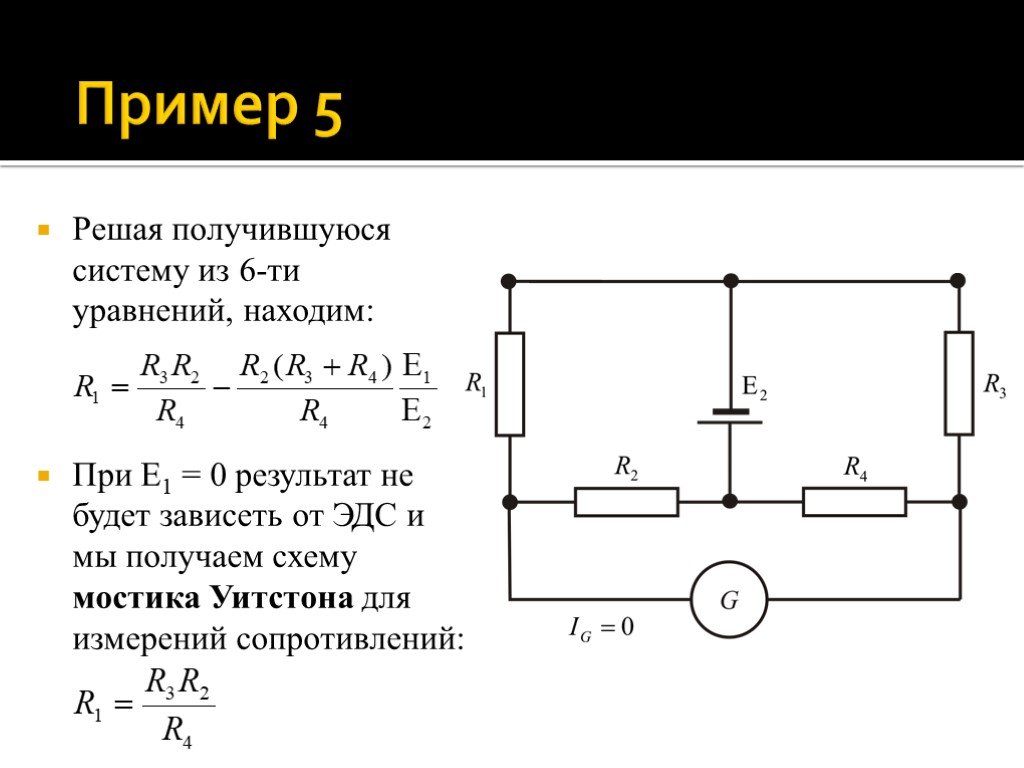
Слайд 55Решая получившуюся систему из 6-ти уравнений, находим: При 1 = 0 результат не будет зависеть от ЭДС и мы получаем схему мостика Уитстона для измерений сопротивлений:
Слайд 563.5 Закон Джоуля - Ленца
Слайд 57Постановка задачи
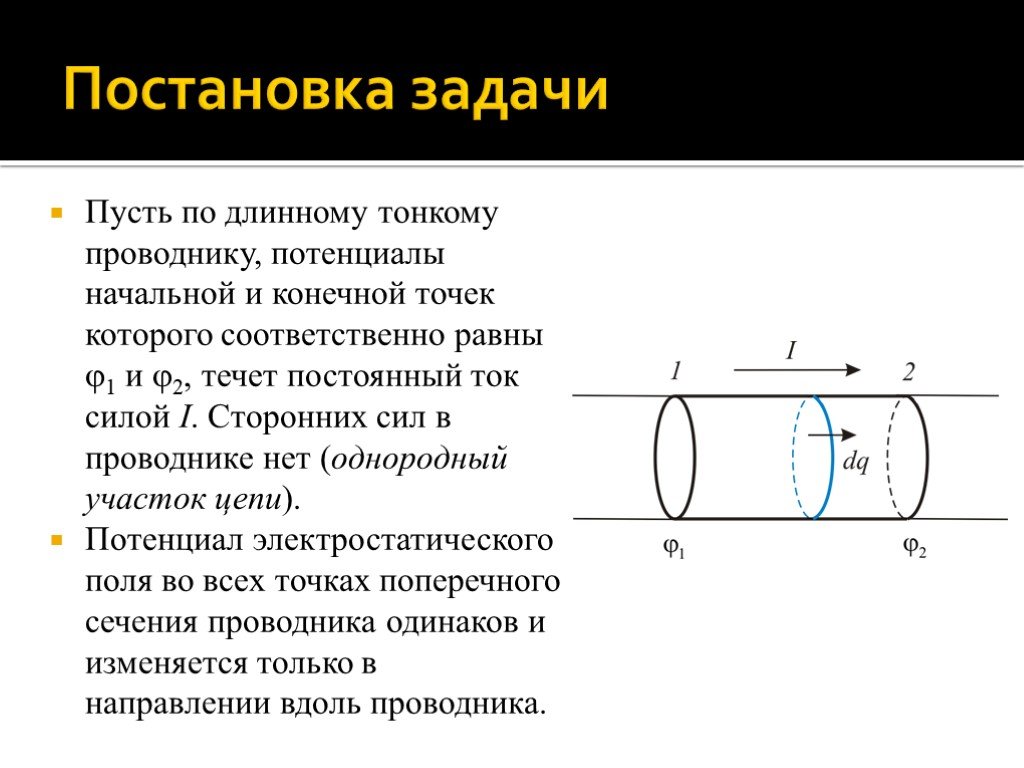
Пусть по длинному тонкому проводнику, потенциалы начальной и конечной точек которого соответственно равны 1 и 2, течет постоянный ток силой I. Сторонних сил в проводнике нет (однородный участок цепи). Потенциал электростатического поля во всех точках поперечного сечения проводника одинаков и изменяется только в направлении вдоль проводника.
Слайд 58Работа тока
За промежуток времени dt через любое поперечное сечение проводника перемещается один и тот же заряд dq, причем dq = Idt. На малом перемещении силы электростатического поля совершают работу dq( –d), где –d - убыль потенциала. Тогда работа электростатических сил на участке 1-2:
Слайд 59Работа и мощность тока
Работой тока на участке электрической цепи называет работа сил электростатического поля, совершаемая при перемещении заряда dq по этому участку: Мощность тока – работа тока, отнесенная к единице времени:
Слайд 60Совершаемая силами поля работа A переходит целиком во внутреннюю энергию проводника при условии что: на участке цепи не действуют внешние силы; не совершается макроскопическая работа. Проводник при этом получает количество теплоты Q = A.
Слайд 61Механизм превращения энергии
Слайд 62Тепловая мощность тока
Количество теплоты Q, выделившееся за время dt на однородном участке проводника, равно работе тока A на этом участке: Тепловая мощность тока, т.е. количество теплоты, выделяющееся на однородном участке цепи в единицу времени:
Слайд 63Закон Джоуля - Ленца
С учетом закона Ома для однородного участка цепи, U = IR, где U = 1 – 2, где R – его сопротивление, I – сила тока, то тепловую мощность можно представить в виде: Закон Джоуля – Ленца (1841 г): выделяющаяся за время t в проводнике с сопротивлением R при протекании по нему тока силой I количество теплоты Q равно
Слайд 64Закон Джоуля – Ленца в локальной форме
Применим формулу тепловой мощности тока к небольшому участку тонкого проводника цилиндрической формы длиной dl и площадью поперечного сечения dS.
Слайд 65Тепловая мощность P в рассматриваемой части проводника с сопротивлением dR равна: Здесь dI – сила тока, текущего по рассматриваемой части проводника. Принимая в внимание выражения для плотности тока и сопротивления, преобразуем выражение для P:
Слайд 66Здесь dV = dSdl – объем цилиндрической части проводника. Удельная тепловая мощность тока – выделяющееся в единицу времени в единице объема проводника количество теплоты: Эта формула выражает закон Джоуля – Ленца в локальной форме (характеризует тепловую мощность тока в точке проводника с данной плотностью тока)
Слайд 67Используя закон Ома в локальной форме j = -1E, где E – напряженность электрического поля в данной точке проводника, закон Джоуля – Ленца в локальной форме можно переписать в следующей форме:
Слайд 68Неоднородный участок цепи
Если участок цепи содержит источник ЭДС, то на носители тока будут действовать как электрические, так и сторонние силы. Тогда, согласно закону сохранения энергии, выделяемое в проводнике тепло будет равно алгебраической сумме работ электрических и сторонних сил. Умножим уравнение закона Ома для неоднородного участка цепи на ток I:
Слайд 69Здесь Pтепл = I2R – выделяющаяся на участке тепловая мощность; Pист = IE – мощность источника тока – мощность, развиваемая на данном участке сторонними силами. Сумма в правой части уравнения, т.е. сумма мощностей электрических и сторонних сил называется мощностью тока на участке цепи.
Слайд 70Если применить данное уравнение ко всей неразветвленной цепи (замкнутой цепи, т.е. когда 1 – 2 = 0), то Т.е. общее количество выделяемой за единице времени по всей цепи джоулевой теплоты равно мощности только сторонних сил. Теплота производится только сторонними силами. Роль же электрических сил сводится к перераспределению этого тепла по различным участкам цепи.
Слайд 71Если умножить обе части закон Ома в локальной форме для неоднородного участка цепи на j, то получим удельную тепловую мощность в неоднородной проводящей среде:
Слайд 723.6 Переходные процессы в цепи с конденсатором
Слайд 73Квазистационарный электрический ток
Законы Ома и Джоуля – Ленца экспериментально были установлены в опытах с постоянным током. Однако они оказываются справедливы и в случае медленно меняющихся токов, которые называются квазистационарными. Текущий по проводнику ток называется квазистационарным, если мгновенное значение силы тока I(t) одинаково во всех поперечных сечениях ветви цепи в один и тот же момент времени.
Слайд 74Условие квазистационарности
Рассмотрим проводник в током, сила которого меняется с течением времени. Обозначим: - характерное изменение силы тока (период T, если ток изменяется по гармоническому закону; время, за которое ток уменьшается в e раз в случае разрядки конденсатора и т .д.). Пусть приложенное к концам проводника напряжение мгновенно изменилось, т.е. произошел скачок напряжения. Новому значению напряжения (разности потенциалов) на концах проводника будет соответствовать новое значение напряженности E, плотности тока j (j = E) и силы тока I (I = jS)

Слайд 75Чтобы текущий в проводнике ток был квазистационарным, изменение тока во всех сечениях проводника в ответ на измененное напряжение должно произойти быстро, а именно: время tуст установления новой величины силы тока в проводнике должно быть мало по сравнение с характерным временем силы тока: Величину tуст можно оценить как время распространения вдоль проводника электромагнитного возмущения – скачка напряженности электрического поля. Скорость этого процесса равна скорости c электромагнитной волны в вакууме.
Слайд 76Таким образом, если l – характерны размер электрической цепи, то время распространения вдоль нее электромагнитного возмущения равно и условие квазистационарности примет вид: Если l ~ 3 м, то при c = 3 108 м/с время tуст установления в проводнике новых стационарных значений E, j и I равно 10-8 с. Таким образом, в проводнике с такими размерами ток можно сыитать квазистационарым, если характерное время его изменения много больше 10-8 с.
Слайд 77Переходные процессы
Рассмотрим пример использования закона Ома для описания переходных процессов в электрических цепях, т.е. процессов, в результате которых сила тока изменяется от одного стационарного значения до другого после скачкообразного изменения внешних параметров цепи.
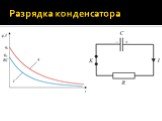
Слайд 78Разрядка конденсатора
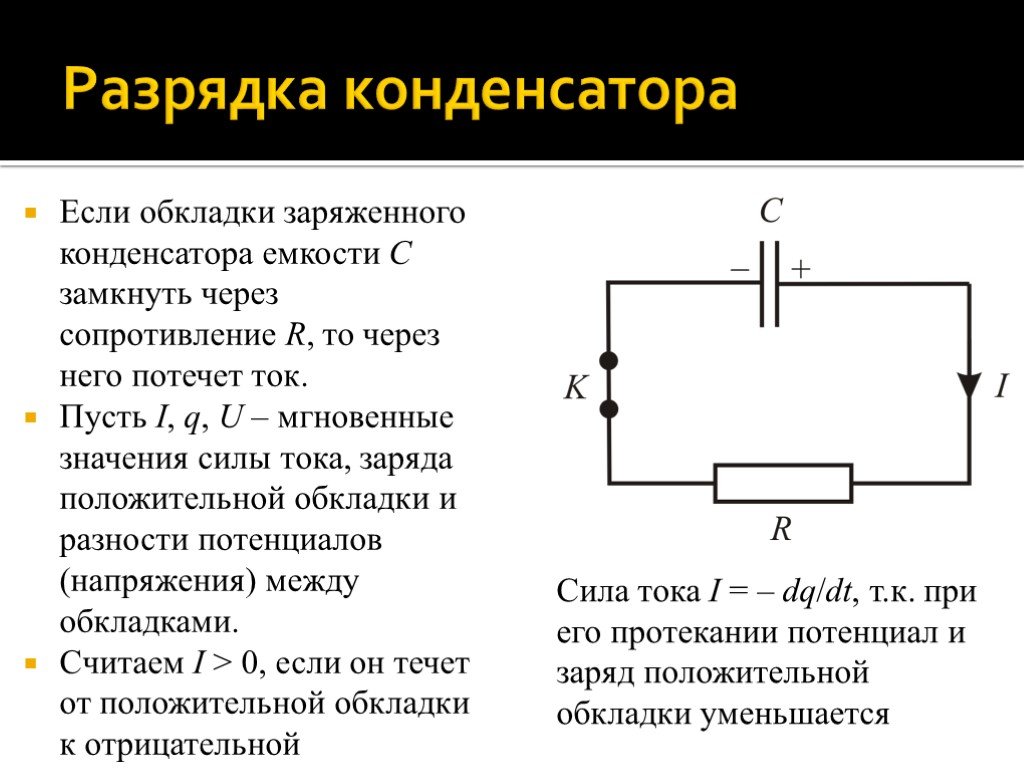
Если обкладки заряженного конденсатора емкости C замкнуть через сопротивление R, то через него потечет ток. Пусть I, q, U – мгновенные значения силы тока, заряда положительной обкладки и разности потенциалов (напряжения) между обкладками. Считаем I > 0, если он течет от положительной обкладки к отрицательной
Сила тока I = – dq/dt, т.к. при его протекании потенциал и заряд положительной обкладки уменьшается
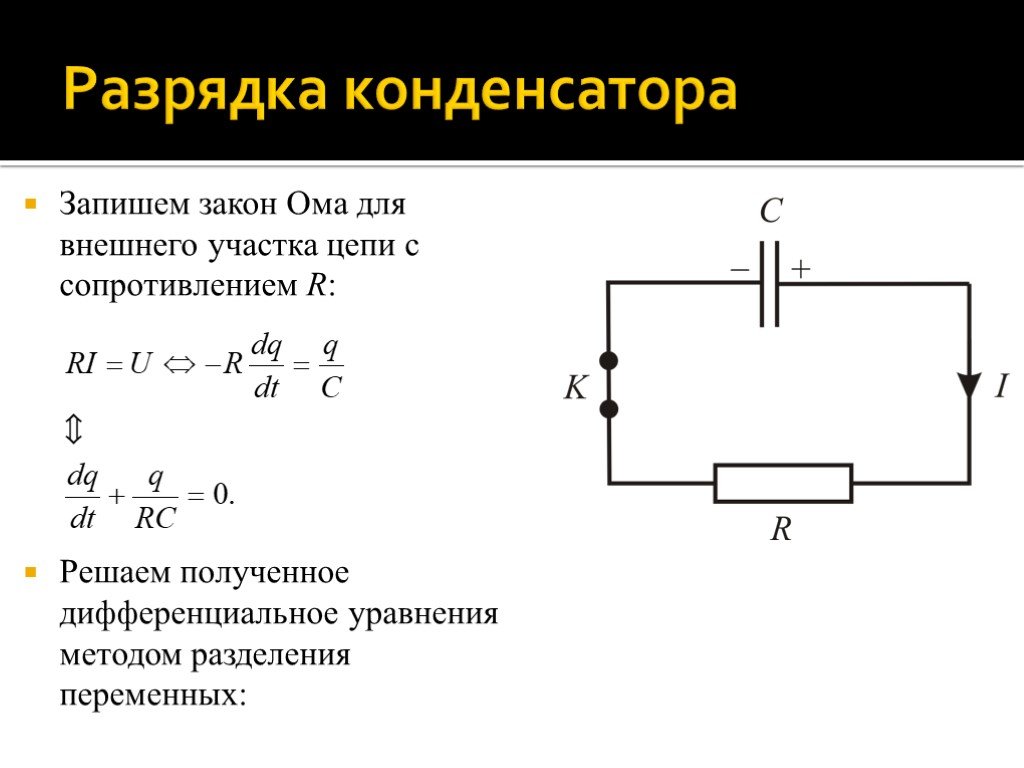
Слайд 79Запишем закон Ома для внешнего участка цепи с сопротивлением R: Решаем полученное дифференциальное уравнения методом разделения переменных:
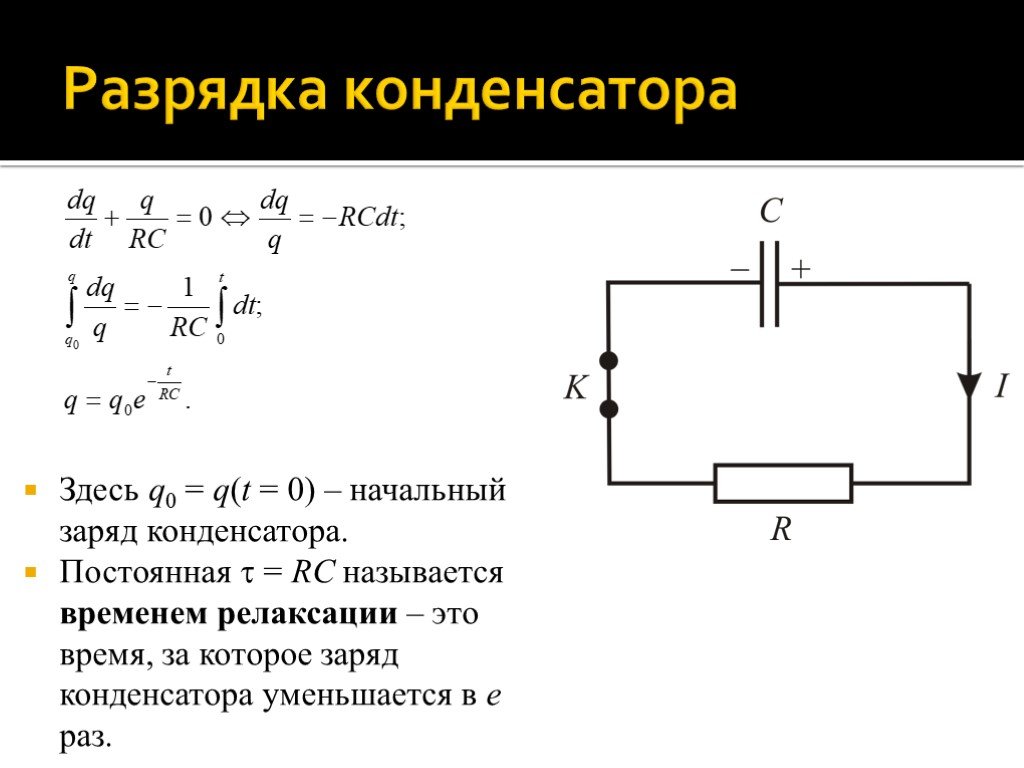
Слайд 80Здесь q0 = q(t = 0) – начальный заряд конденсатора. Постоянная = RC называется временем релаксации – это время, за которое заряд конденсатора уменьшается в e раз.
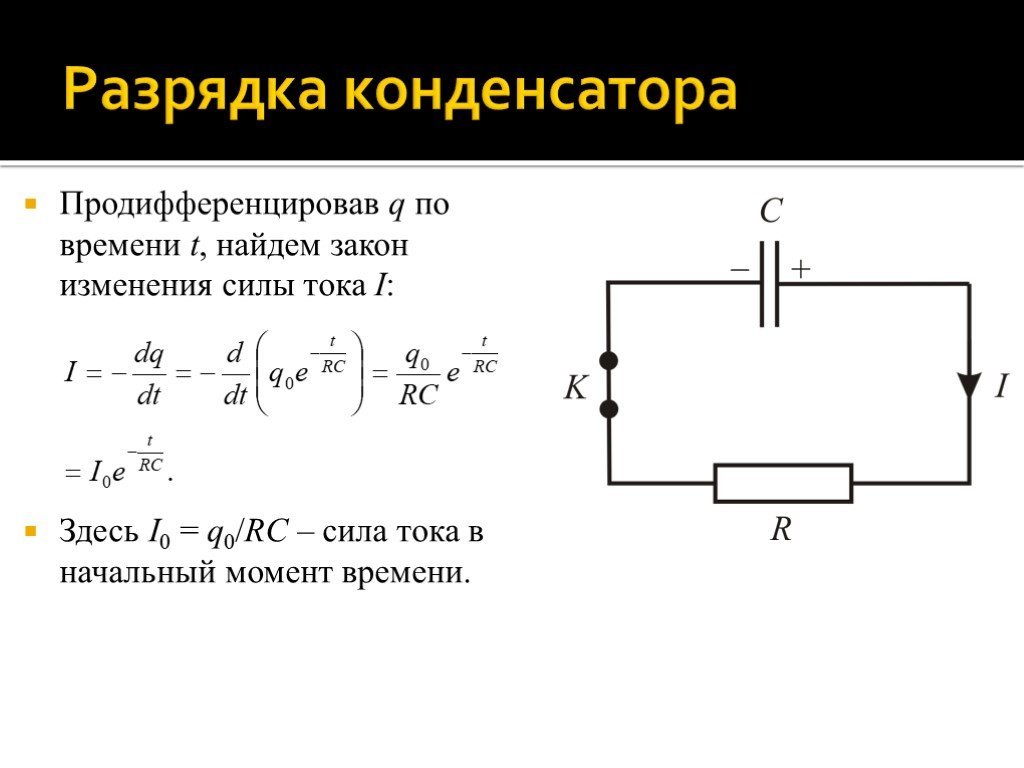
Слайд 81Продифференцировав q по времени t, найдем закон изменения силы тока I: Здесь I0 = q0/RC – сила тока в начальный момент времени.
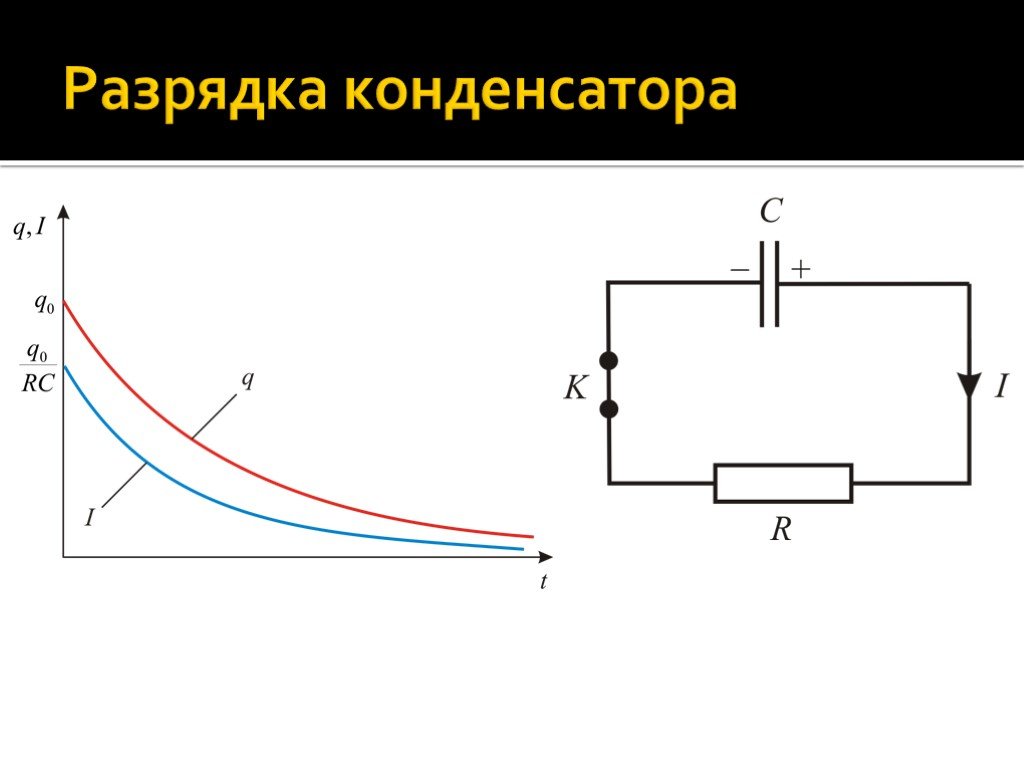
Слайд 82
Слайд 83Зарядка конденсатора
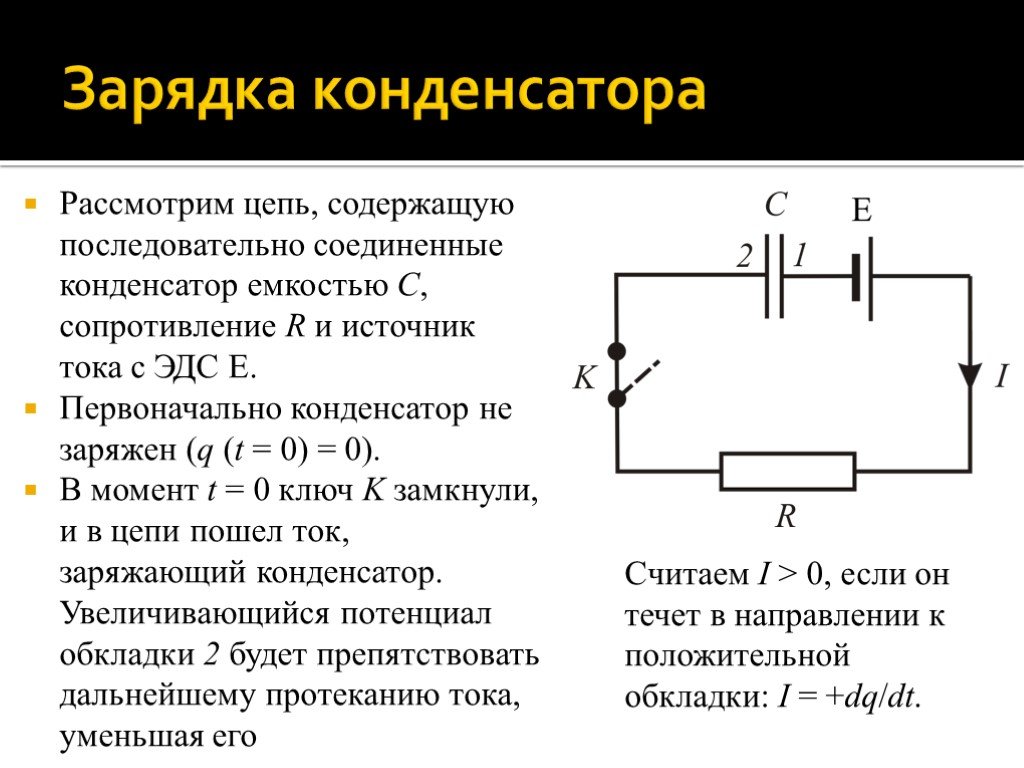
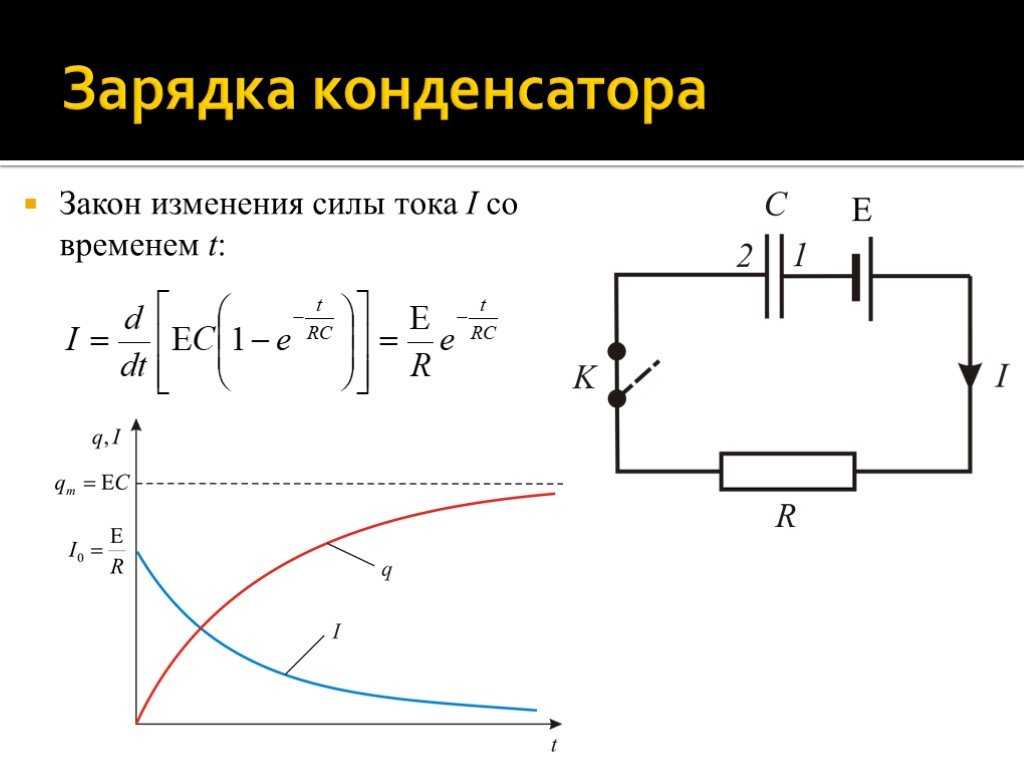
Рассмотрим цепь, содержащую последовательно соединенные конденсатор емкостью C, сопротивление R и источник тока с ЭДС E. Первоначально конденсатор не заряжен (q (t = 0) = 0). В момент t = 0 ключ K замкнули, и в цепи пошел ток, заряжающий конденсатор. Увеличивающийся потенциал обкладки 2 будет препятствовать дальнейшему протеканию тока, уменьшая его
Считаем I > 0, если он течет в направлении к положительной обкладки: I = +dq/dt.
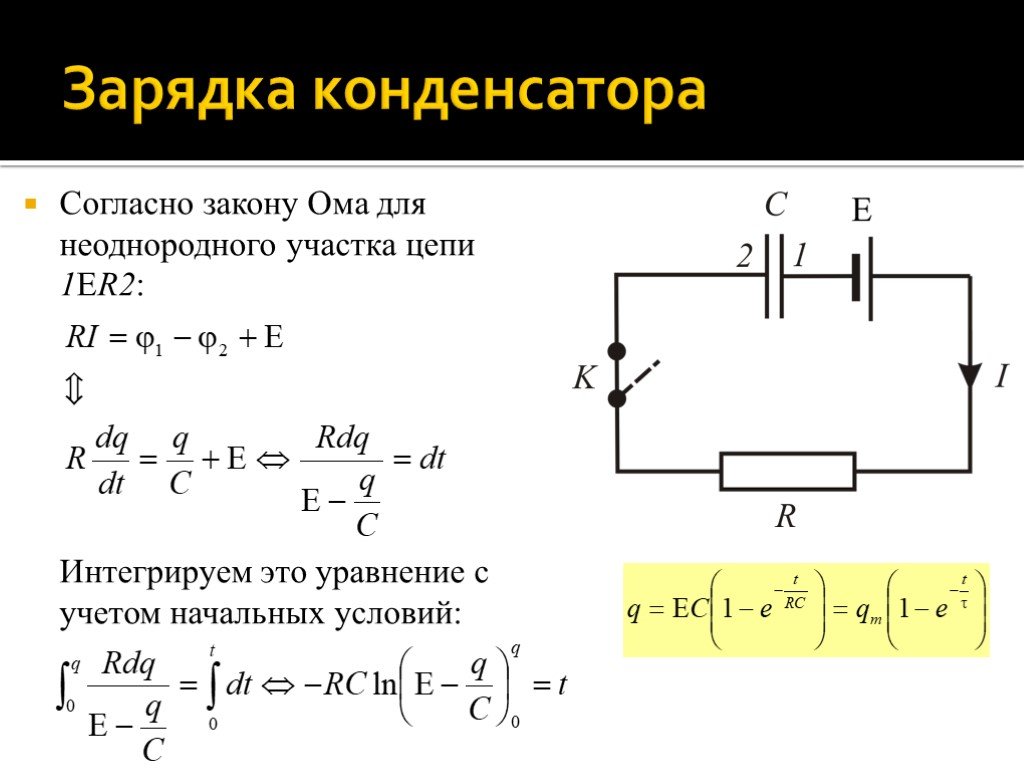
Слайд 84Согласно закону Ома для неоднородного участка цепи 1ER2: Интегрируем это уравнение с учетом начальных условий:
Слайд 85Закон изменения силы тока I со временем t: