Презентация "Непрерывная случайная величина. Числовые характеристики. Законы распределения." – проект, доклад
Презентацию на тему "Непрерывная случайная величина. Числовые характеристики. Законы распределения." можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
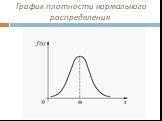
Непрерывная случайная величина (НСВ)
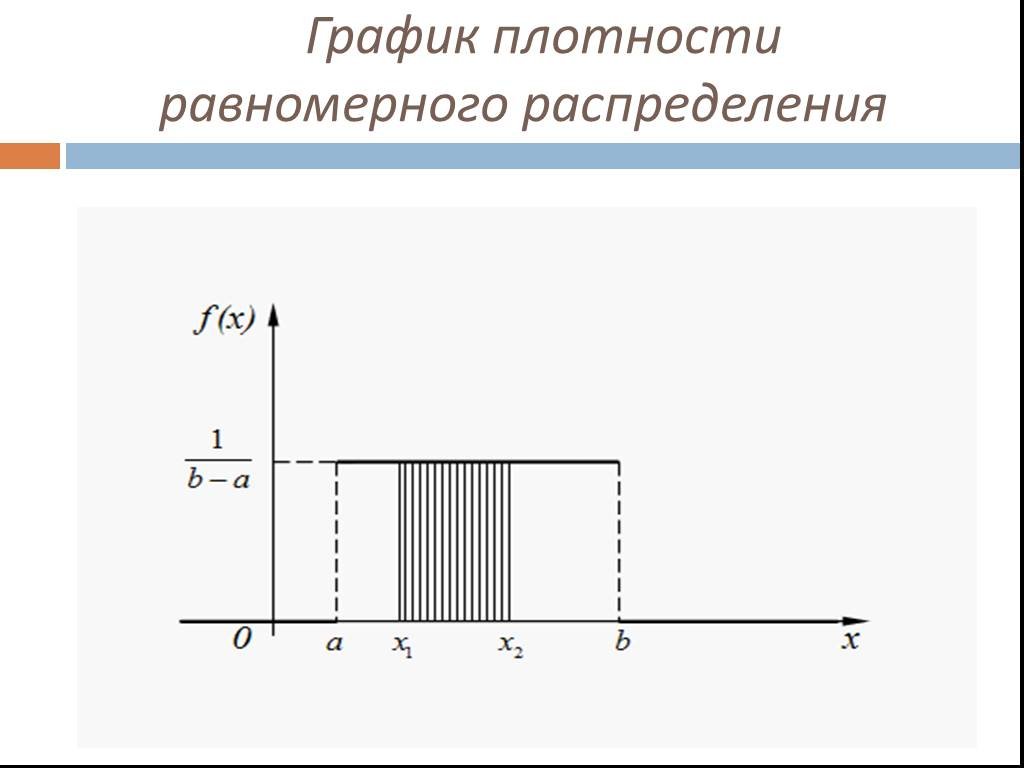
1. С помощью интегральной функции распре-деления (или функции распределения) F(x). 2. С помощью дифференциальной функции рас-пределения (или плотности ...Числовые выражения
. . ...Тема 3. Законы, закономерности и принципы менеджмента
1. Законы и закономерности менеджмента. Всем, что нас окружает, управляют объективные законы - существенные, устоявшиеся, повторяющиеся отношения ...Строение и характеристики машин
1. Машины. Уже несколько веков существование человечества невозможно представить без машин – устройств, различных по назначению и конструкции. Но, ...Статические и динамические характеристики элементов и систем
К регуляторам предъявляются определенные требования, относящиеся к качеству процесса регулирования. Показателями качества процесса регулирования являются ...Реклама: цели, задачи, функции и основные характеристики
Реклама - это убеждающее средство информации о товарах или фирме, коммерческая пропаганда потребительских свойств товара и достоинств фирмы, готовящая ...Миграционные процессы в РФ, их характеристики и тенденции
Миграция населения (от лат. migratio – переселение) - перемещение людей (мигрантов) через границы тех или иных территорий с переменой места жительства ...Метрологические характеристики средств измерений
введения поправок): - Функция преобразования измерительного преобразователя, а также измерительного прибора с неименованной шкалой; - Значение однозначной ...Количественные характеристики преступности
Состояние и уровень преступности. Состояние преступности – (в широком смысле) вся совокупность ее количественно-качественных показателей, (в узком ...Законы семьи
Задачи собрания:. формировать нравственную культуру детей и родителей; способствовать развитию коммуникативных умений, доброты и взаимопонимания в ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 февраля 2019
Категория:Разные
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию