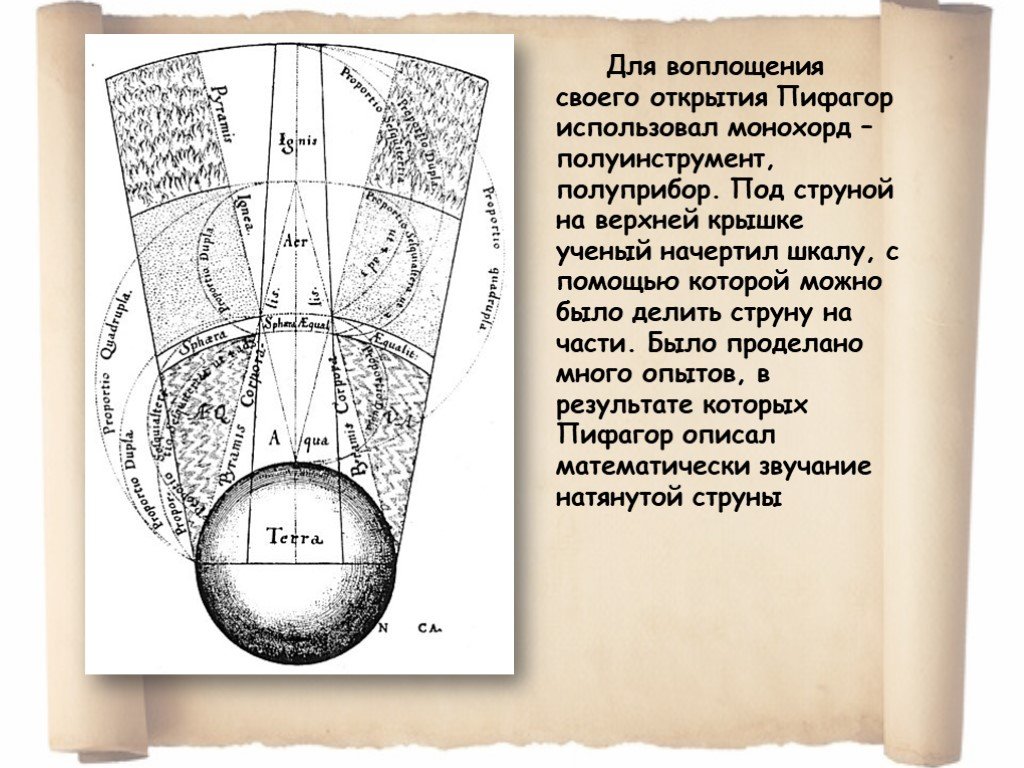
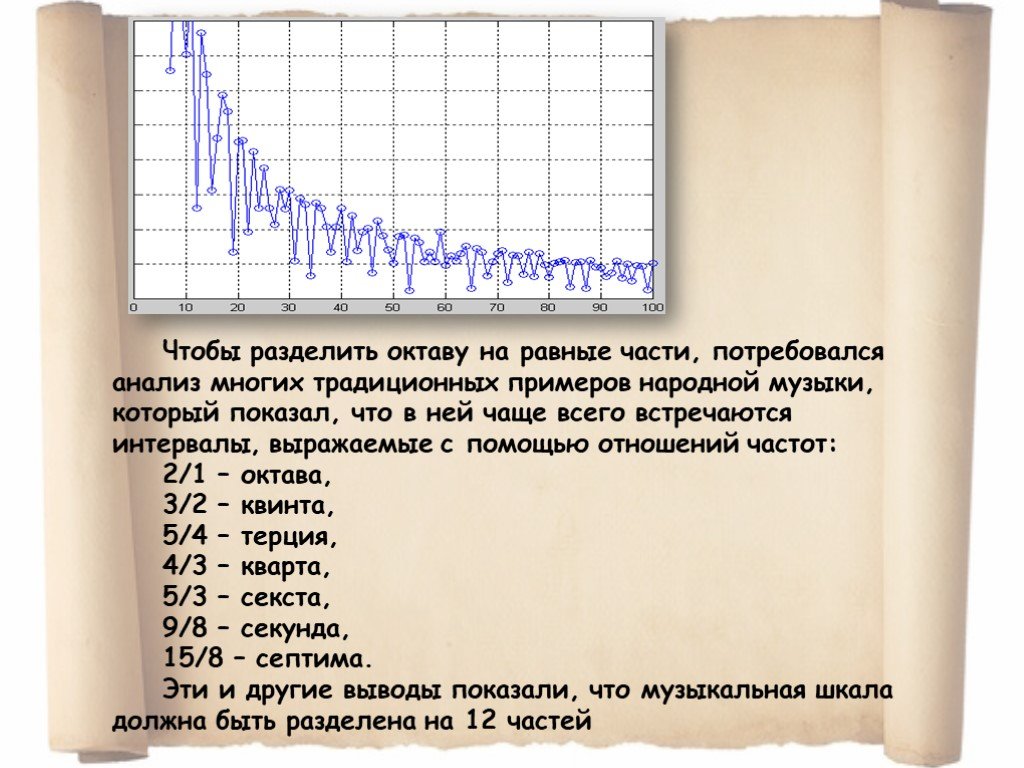
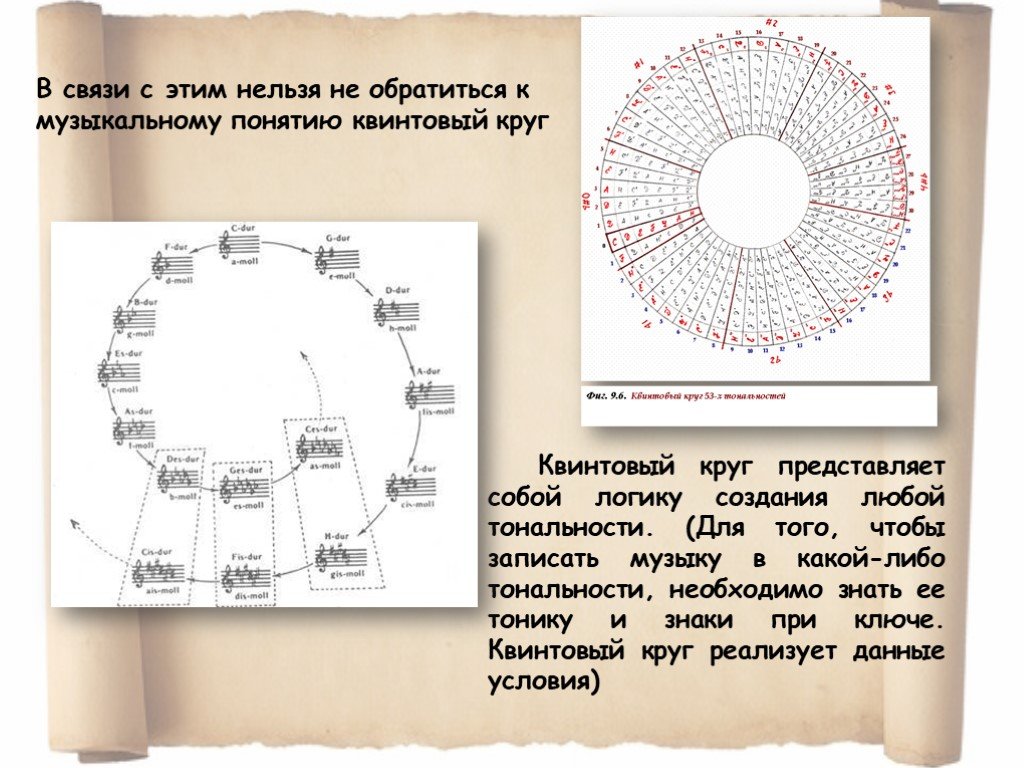
Презентация "Связь математики и музыки" (7 класс) по музыке – проект, доклад
Презентацию на тему "Связь математики и музыки" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Музыка. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 32 слайд(ов).
Слайды презентации
Список похожих презентаций
Мелодия - душа музыки
Назови музыкальные жанры. Песня Марш Танец. Вот вплывает песня-кит Словно реченька журчит. Очень ласково поет Даже за сердце берет. песня. У каждого ...Музыкально-ритмические игры и упражнения на уроках музыки
“Музыкальное творчество детей – самый действенный способ их развития”. (Б. В. Асафьев. ). Сказки о музыке к урокам. «Как, мальчик познакомился с нотками» ...Характеристика музыкального зала и кабинета музыки
МУЗЫКАЛЬНЫЙ РУКОВОДИТЕЛЬ МОКШАНОВА СВЕТЛАНА НИКОЛАЕВНА ОБРАЗОВАНИЕ – ВЫСШЕЕ ПЕДАГОГИЧЕСКИЙ СТАЖ РАБОТЫ-29 ЛЕТ. Там, где слова бессильны, является ...В чём сила музыки
«Без музыки Земля – пустой, недостроенный дом, в котором никто не живёт» (Л.Тик). Музыка – искусство, обладающее большой силой эмоционального воздействия ...Путешествие в мир музыки
Здравствуй, добрый нотный дом! - Кто живет здесь? - Мы живем! - Дружно ноты говорят, Собираясь в звукоряд. В дом нам хочется войти, Но преграда на ...Современный урок музыки
Системно-деятельностный подход. 1) опирается на зону ближайшего развития; 2) учащийся действует как субъект собственной учебной деятельности; 3) обучение ...Воздействие музыки на человека
Актуальность:. В силу особенности средств музыкальной выразительности, их влияния на психику, способности музыки, как никакого другого вида искусства, ...Построение (формы) музыки
Музыкальные формы. Одночастные Двухчастные Трехчастные Четырехчастные Рондо Вариации. Одночастная форма. Нет изменения характера музыки Песня без ...Влияние музыки на организм человека
Цель и задачи реферата. Цель: выявление позитивных и негативных сторон влияния музыки на организм человека. Задачи: - изучить информационные источники ...Влияние музыки на человека
Я учусь в музыкальной школе во втором классе, обучаюсь игре на баяне, играю в трио баянистов, в оркестре . В музыкальную школу пошел учиться с большим ...Влияние музыки на настроение человека
Цель исследования:. узнать как музыка может повлиять на настроение человека? Задача:. узнать какую музыку нужно слушать для поднятия настроения; узнать ...Влияние музыки на здоровье человека
Музыка окружает человека во всех сферах его жизни и во все времена. Еще с древних времен люди применяли целебные воздействия музыкальных композиций ...В чем сила музыки Джулио Каччини? Урок музыки в 6 классе
Цели и задачи. Цель урока Показать взаимосвязь иконописи и музыки Средствами музыкальной выразительности показать воплощение образа матери в светском ...Неделя музыки
Название проекта: «Неделя музыки» Тип проекта: Творческий . Продолжительность проекта: Краткосрочный (одна неделя) Участники проекта: музыкальный ...Возможности Интернета для организации образовательного процесса на уроках музыки
Компьютерные программы, используемые при подготовке и проведении уроков музыки:. Microsoft Word Microsoft Power Point Internet Explorer Проигрыватель ...Образ музыки в симфонии №7 «Ленинградская» Д.Шостаковича
Дмитрий Дмитриевич Шостакович 1906 - 1975. “Музыка Шостаковича – это мир глубоких… мыслей…, это гимн человеку…, это протест против жестокости…, это ...Воспитательный потенциал урока музыки
«Знания без воспитания – меч в руках сумасшедшего». Д.И. Менделеев. ЗНАНИЯ ВОСПИТАНИЕ. Федеральные государственные образовательные стандарты. Начальное ...Преобразующая сила музыки
Музыка способна оказывать огромное воздействие на людей. Она может выразить состояние души человека- веселье и печаль, радость и тоску, волнение и ...Выдающиеся исполнители музыки
Кто это? Певческие мужские голоса. С.Я.Лемешев. биография. ЛЕМЕШЕВ Сергей Яковлевич родился 27 VI (10 VII)1902, в деревне Старое Князево, Тверской ...Развитие творческих способностей на уроках музыки
Причины обращения к проблеме: неудовлетворённость творческими способностями учащихся. Цели и задачи развития творческих способностей учащихся. Музыкальное ...Конспекты
Взаимосвязь музыки и литературы
. Государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа № 29 города Сызрани городского округа ...Связь музыки и изобразительного искусства
Муниципальное общеобразовательное учреждение Ильинская средняя общеобразовательная школа. Технологическая карта урока. Предмет:. музыка. Класс:. ...Роль музыки и музыкального сопровождения на занятиях по ритмике
. Роль музыки и музыкального сопровождения. на занятиях по ритмике. Музыка занимает одно из центральных мест при проведении ритмических ...Путешествие в страну музыки
Мунициапальное Дошкольное Образовательное Учреждение –. детский сад № 17. . Конспект урока музыки на тему. «Путешествие в страну ...Путешествие в мир знакомой музыки
МУНИЦИПАЛЬНОЕ. . ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА. с углубленным изучением отдельных предметов №78. городского ...Проблемные диалоги на уроках музыки
Учитель музыки высшей категории МБОУ « СОШ №30. . с углублённым изучением отдельных предметов». . Энгельсского муниципального района Саратовской ...Преобразующая сила музыки
МБОУ «Средняя общеобразовательная средняя школа № 18. . г. Абакана Республики Хакасия». . . . . . Конспект урока музыки для 5 класса ...Общность жанров инструментальной и вокальной музыки
Конспект урока по музыке для 5 класса. Тема урока:. «Общность жанров инструментальной и вокальной музыки». Тип урока:. урок ознакомления с новым ...Мир музыки М.И.Глинки. Вальс-фантазия
Государственное общеобразовательное учреждение. средняя общеобразовательная школа №604. с углубленным изучением предметов. художественно-эстетического ...Для музыки разных стран нет непереходимых границ
Учитель музыки 1-ой категории МОУ СОШ п. Дружба. Дятьковского района, Брянской области Новиков Алексей Александрович. Обобщающий урок музыки ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 сентября 2018
Категория:Музыка
Содержит:32 слайд(ов)
Поделись с друзьями:
Скачать презентацию