Слайд 1
Слайд 2Объёмы тел Изображения пространственных фигур
СТЕРЕОМЕТРИЯ
Слайд 3Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления — это ключ к изучению стереометрии
«Мой карандаш, бывает еще остроумней моей головы», — признавался великий математик Леонард Эйлер (1707—1783).
В своей деятельности человеку повсюду приходится сталкиваться с необходимостью изучать форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул. Раздел геометрии, в котором изучаются такие задачи, называется стереометрией
Слайд 4ГЕОМЕТРИЯ возникла из практических задач людей; ГЕОМЕТРИЯ лежит в основе всей техники и большинства изобретений человечества; ГЕОМЕТРИЯ нужна
технику, инженеру, рабочему, архитектору, модельеру …
Мы знаем, что
Слайд 5ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ на плоскости
ГЕОМЕТРИЯ в пространстве
«планиметрия» – наименование смешанного происхождения: от греч. metreo – измерять и лат. planum – плоская поверхность (плоскость)
«стереометрия» – от греч. stereos – пространственный (stereon – объем).
ГЕОМЕТРИЯ
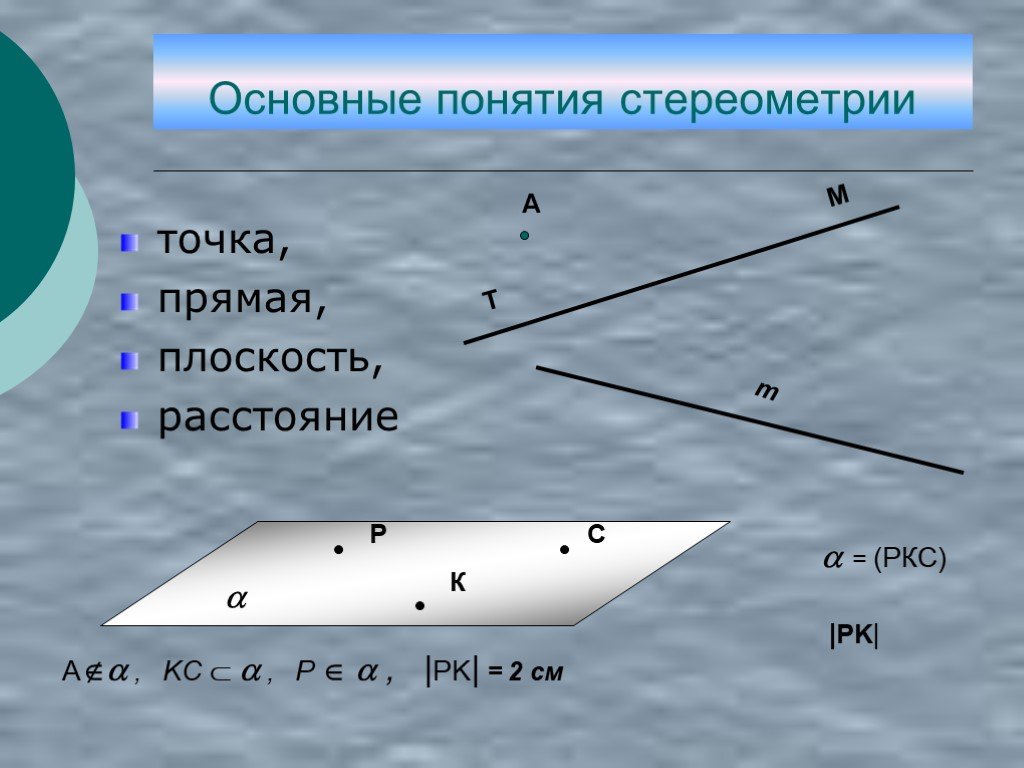
Слайд 6Основные понятия стереометрии
точка, прямая, плоскость, расстояние
= (РКС) |PK|
A , KC , P , |PK| = 2 см
Слайд 7Аксиомы стереометрии
Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное положение теории.
Понятия «точка», «прямая», «плоскость», «расстояние» принимаются без определений: их описание и свойства содержатся в аксиомах
Система аксиом стереометрии дает описание свойств пространства и основных его элементов
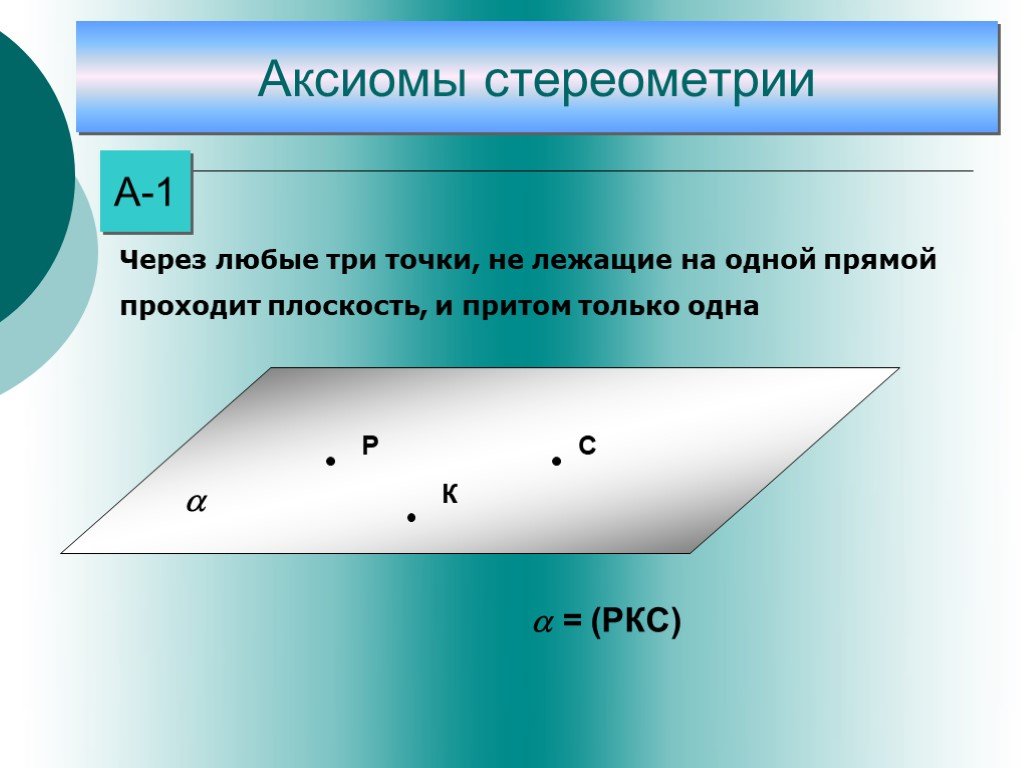
Слайд 8А-1
Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом только одна
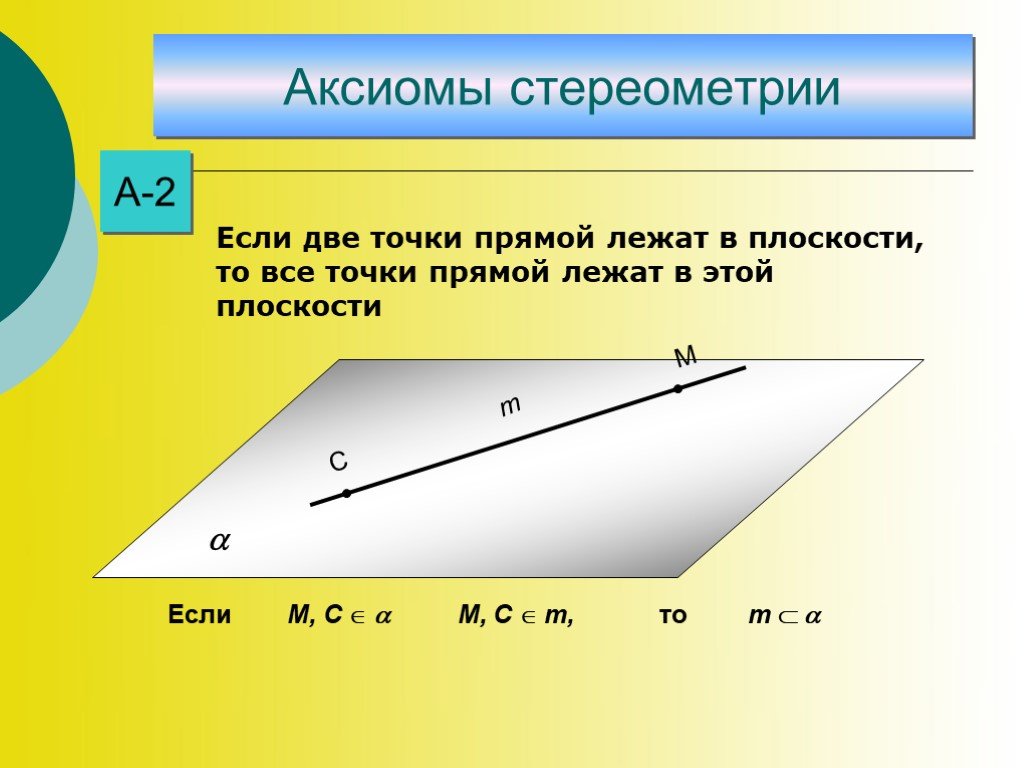
Слайд 9А-2 m М, C m М, C m, Если то
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
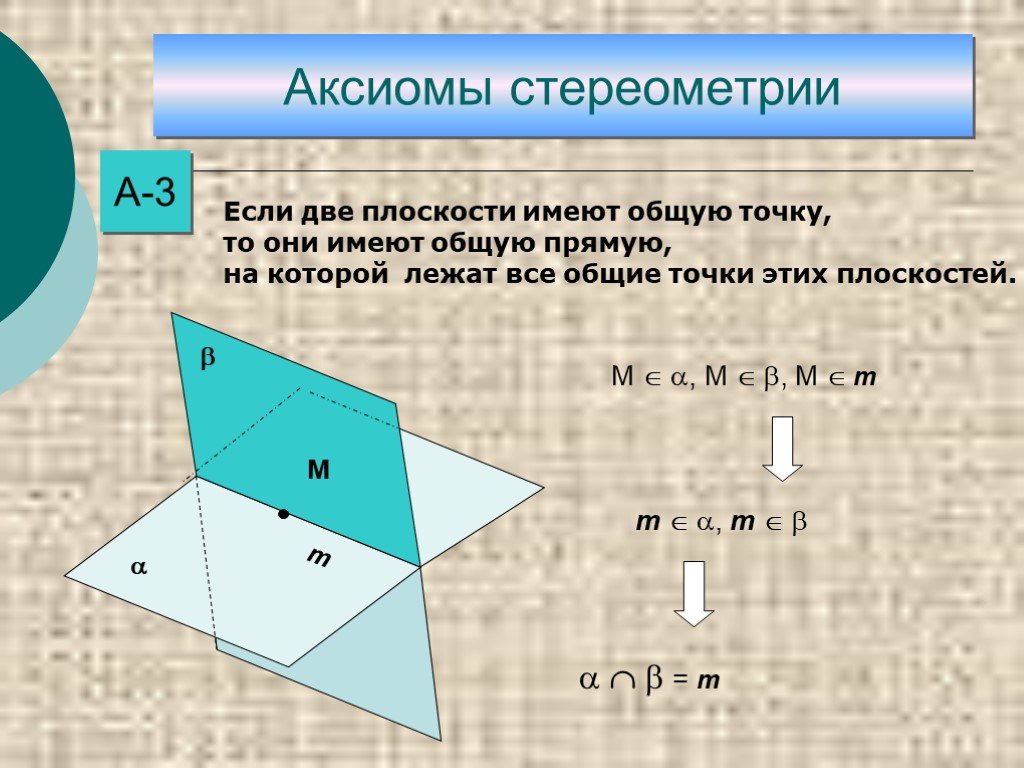
Слайд 10А-3 М , М , М m m , m = m
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Слайд 11СЛЕДСТВИЯ ИЗ АКСИОМ
Т-1
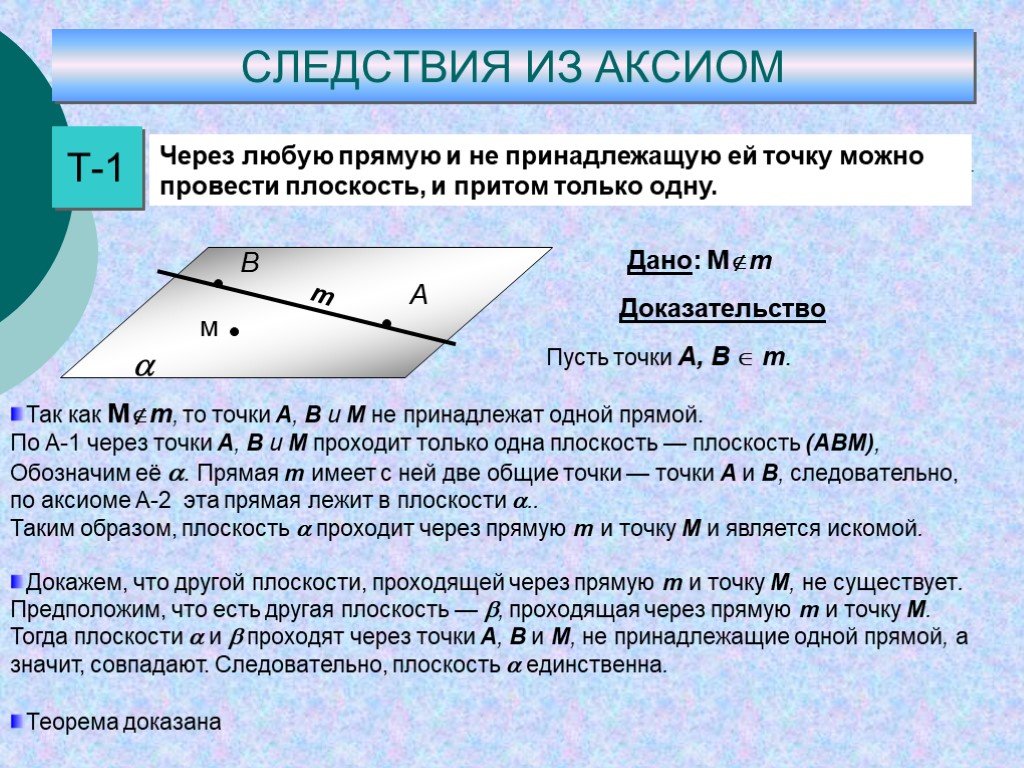
Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.
м А В Дано: Мm
Так как Мm, то точки А, В и M не принадлежат одной прямой. По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM), Обозначим её . Прямая m имеет с ней две общие точки — точки A и B, следовательно, по аксиоме А-2 эта прямая лежит в плоскости .. Таким образом, плоскость проходит через прямую m и точку M и является искомой. Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует. Предположим, что есть другая плоскость — , проходящая через прямую m и точку M. Тогда плоскости и проходят через точки А, В и M, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость единственна. Теорема доказана
Доказательство
Пусть точки A, B m.

Слайд 12Т-2
Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
N Дано: m n = M
Отметим на прямой m произвольную точку N, отличную от М.
Рассмотрим плоскость =(n, N). Так как M и N, то по А-2 m . Значит обе прямые m, n лежат в плоскости и следовательно , является искомой Докажем единственность плоскости . Допустим, что есть другая, отличная от плоскости и проходящая через прямые m и n, плоскость . Так как плоскость проходит через прямую n и не принадлежащую ей точку N, то по T-1 она совпадает с плоскостью . Единственность плоскости доказана. Теорема доказана
Слайд 13По трем точкам, не лежащим на одной прямой По прямой и точке, не лежащей на этой прямой По двум пересекающимся прямым По двум параллельным прямым
ВЫВОД
Как в пространстве можно однозначно задать плоскость?
Слайд 14Определение Тело называется простым, если его можно разбить на конечное число треугольных пирамид. В частности, любой выпуклый многогранник является простым телом.
Определение Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами: равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;
Определение объема тела
Слайд 15за единицу объема принят объем куба, ребро которого равно единице длины; если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;
Определение
Тела с равными объемами называются равновеликими .
Из свойства 2 следует, что если тело с объемом V 1 содержится внутри тела с объемом V 2, то V 1 < V 2.
Слайд 16Теорема 1.
Объем прямоугольного параллелепипеда равен произведению его измерений: V = abc
Теорема 2.
Объем прямой призмы равен произведению площади основания на высоту: V = SH .
Пусть ABCA 1 B 1 C 1 – прямая треугольная призма, причем ее основание – прямоугольный треугольник ABC Дополним эту призму до прямоугольного параллелепипеда ACBDA 1 C 1 B 1 D 1. Середина O диагонали AB 1 этого параллелепипеда является его центром симметрии.
Данная призма и призма ABDA1B1D1, которая дополняет данную призму до параллелепипеда, симметричны относительно точки O , а поэтому равновелики.

Слайд 17Рассмотрим произвольную прямую треугольную призму ABCA1B1C1 Если Δ ABC не прямоугольный, то его можно разбить на два прямоугольных треугольника ADC и BDC . Следовательно, V = V 1 + V 2 = S Δ ADC · H + S Δ BDC · H = SΔ ABC · H = S · H . Таким образом, теорема справедлива для произвольной прямой треугольной призмы. Если есть прямая n -угольная призма ( n > 3), разобьем ее на конечное число прямых треугольных призм Сложив объемы этих треугольных призм, получим объем n -угольной призмы V = V 1 + V 2 + ... + V n = ( S 1 + S 2 + ... + S n ) H = S · H , где S 1, S 2, ..., S n – площади оснований треугольных призм, S и H – площадь основания и высота n -угольной призмы.
Пусть V и V 1 – соответственно объемы призмы ABCA 1 B 1 C 1 и параллелепипеда,
тогда, учитывая теорему1, получим

Слайд 18Рассмотрим произвольную прямую треугольную призму ABCA 1 B 1 C 1 Если Δ ABC не прямоугольный, то его можно разбить на два прямоугольных треугольника ADC и BDC . Следовательно, V = V1 + V2 = SΔ ADC · H + SΔ BDC · H = S Δ ABC · H = S · H . Таким образом, теорема справедлива для произвольной прямой треугольной призмы. Если есть прямая n -угольная призма ( n > 3), разобьем ее на конечное число прямых треугольных призм
Сложив объемы этих треугольных призм, получим объем n -угольной призмы V = V 1 + V 2 + ... + V n = ( S 1 + S 2 + ... + S n ) H = S · H , где S 1, S 2, ..., S n – площади оснований треугольных призм, S и H – площадь основания и высота n -угольной призмы.

Слайд 19Объем наклонной призмы равен площади перпендикулярного сечения на боковое ребро: V = S пс
Пусть ABCA1B1C1 – наклонная призма (чертеж 6.1.4), A2B2C2 и A3B3C3 – перпендикулярные сечения этой призмы. Призма A2B2C2A3B3C3 прямая, причем A2A3=A1A .Заметим, что параллельный перенос на вектор переводит многогранник A 2 B 2 C 2 A 1 B 1 C 1 в многогранник A 3 B 3 C 3 ABC . Следовательно, эти многогранники равновеликие. Пусть V – объем призмы ABCA 1 B 1 C 1, V 1 – объем призмы A 3 B 3 C 3 A 2 B 2 C 2, V 2 – объем многогранника A 2 B 2 C 2 ABC , тогда V + V 2 = V1 + V2, откуда V = V 1. Поскольку призма A 3 B 3 C 3 A 2 B 2 C 2 прямая, то V 1 = S Δ A 3 B 3 C 3 · A 2 A 3 = Sпс · l = V , что и требовалось доказать
Теорема 3.

Слайд 20Объем наклонной призмы равен произведению площади основания на высоту: V = S · H .
Пусть A 2 B 2 C 2 – перпендикулярное сечение наклонной призмы ABCA 1 B 1 C 1, A 1 O – высота этой призмы. Пусть . Поскольку , а , то плоскости A2B2C2 и ABC образуют тот же угол φ, что и прямые A 1 A и A 1 O . По теореме о площади ортогональной проекции SA2B2C2 = S AB С cos φ. Согласно теореме 3 V = S A 2 B 2 C 2 · A 1 A = S AB С cos φ · A 1 A = SABС · A 1 O = S · H .
Теорема 4.
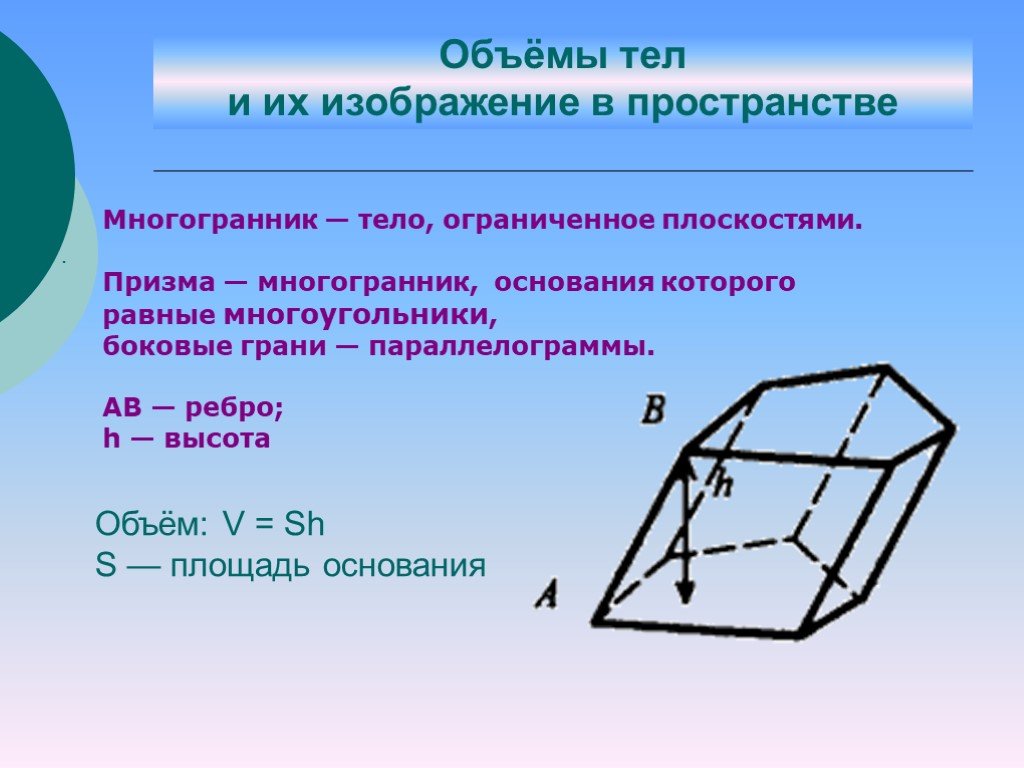
Слайд 21Объём: V = Sh S — площадь основания
Многогранник — тело, ограниченное плоскостями. Призма — многогранник, основания которого равные многоугольники, боковые грани — параллелограммы. АВ — ребро; h — высота
Объёмы тел и их изображение в пространстве
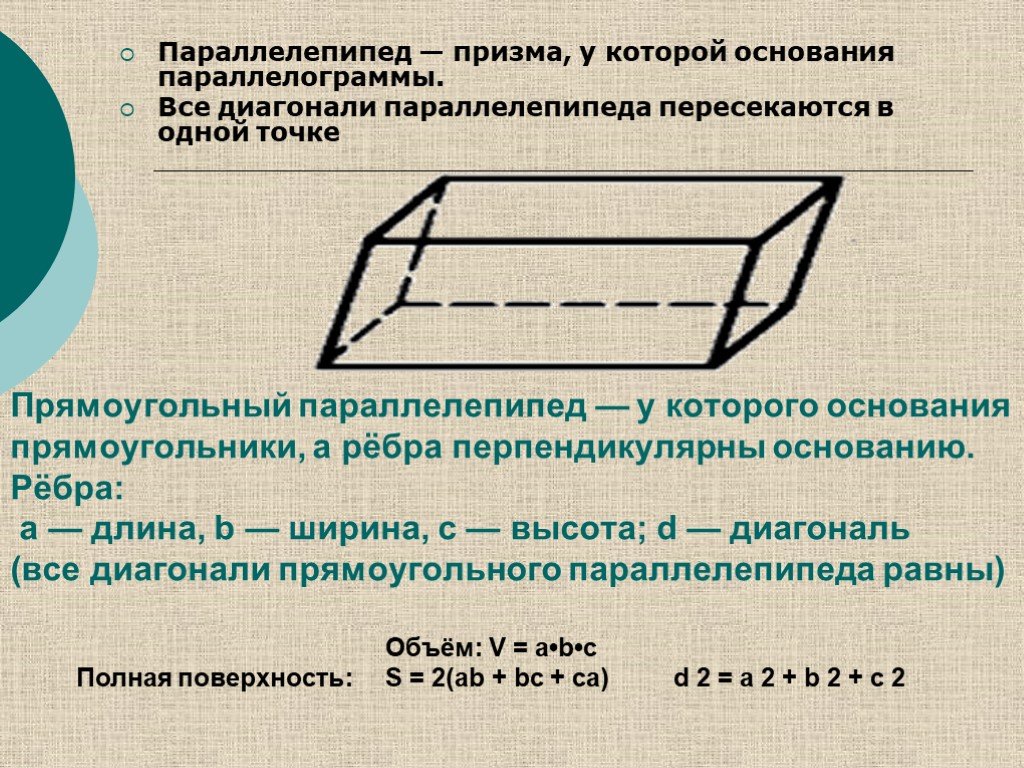
Слайд 22Параллелепипед — призма, у которой основания параллелограммы. Все диагонали параллелепипеда пересекаются в одной точке
Прямоугольный параллелепипед — у которого основания прямоугольники, а рёбра перпендикулярны основанию. Рёбра: а — длина, b — ширина, с — высота; d — диагональ (все диагонали прямоугольного параллелепипеда равны)
Объём: V = a•b•c Полная поверхность: S = 2(ab + bc + ca) d 2 = a 2 + b 2 + c 2
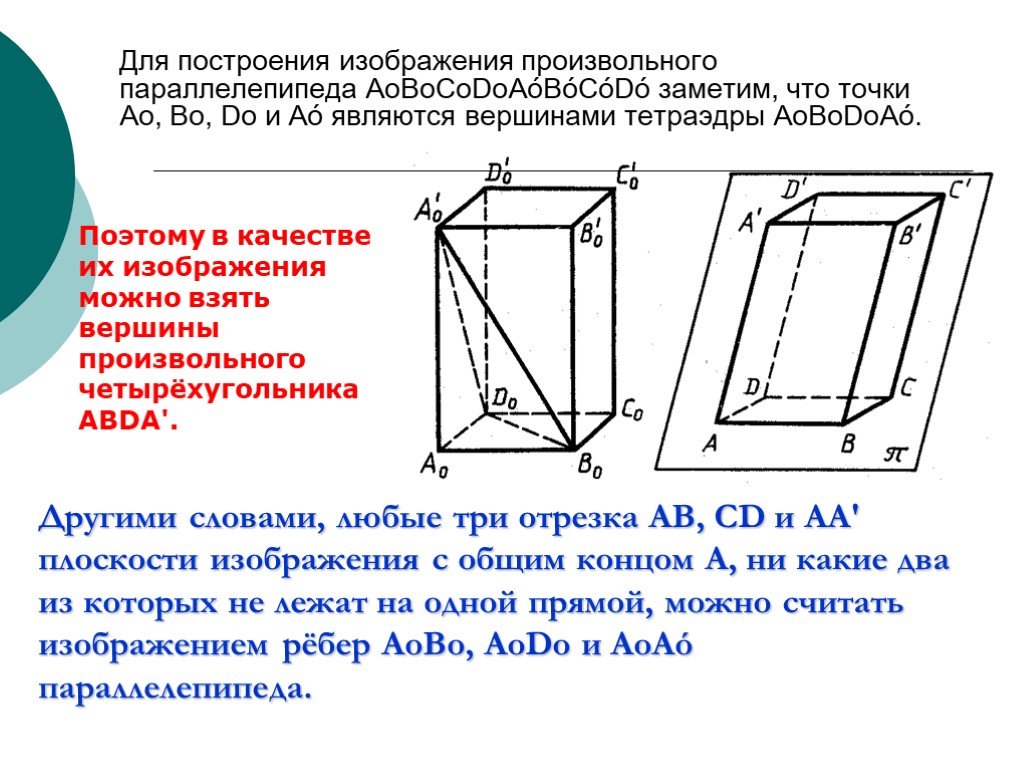
Слайд 23Для построения изображения произвольного параллелепипеда AоBоCоDоAóBóСóDó заметим, что точки Ао, Во, Dо и Аó являются вершинами тетраэдры АоВоDоАó.
Другими словами, любые три отрезка AB, CD и AA' плоскости изображения с общим концом А, ни какие два из которых не лежат на одной прямой, можно считать изображением рёбер AоBо, AоDо и AоАó параллелепипеда.
Поэтому в качестве их изображения можно взять вершины произвольного четырёхугольника АВDА'.
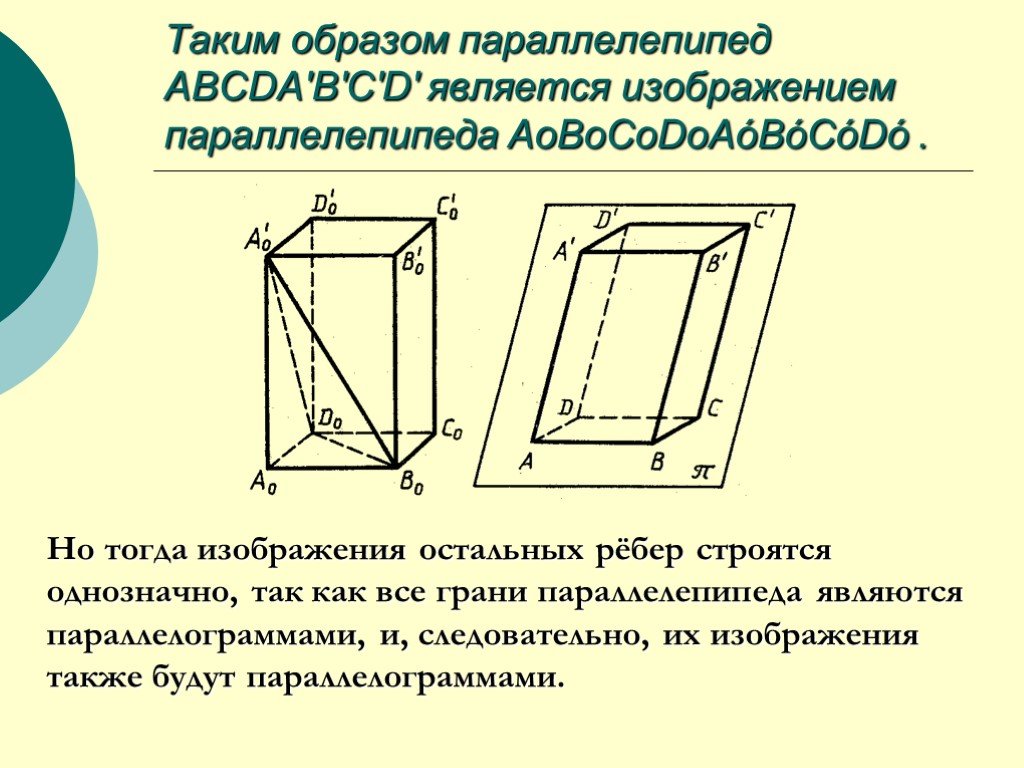
Слайд 24Таким образом параллелепипед ABCDA'B'C'D' является изображением параллелепипеда AоBоCоDоAóBóСóDó .
Но тогда изображения остальных рёбер строятся однозначно, так как все грани параллелепипеда являются параллелограммами, и, следовательно, их изображения также будут параллелограммами.
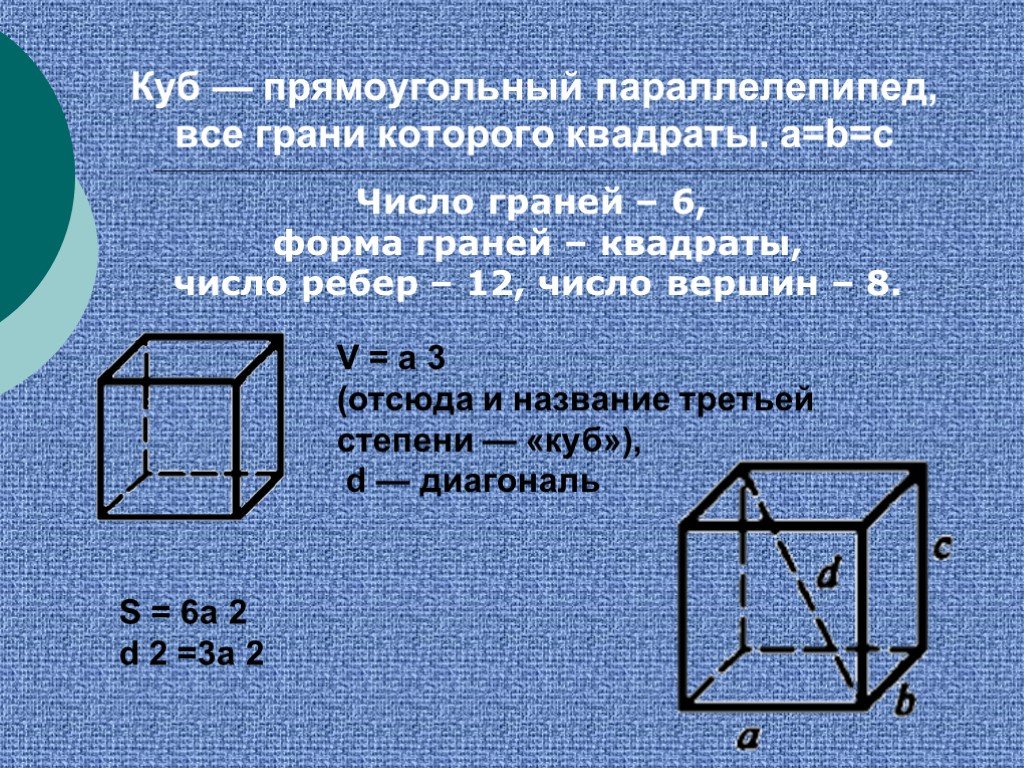
Слайд 25Куб — прямоугольный параллелепипед, все грани которого квадраты. а=b=с
V = а 3 (отсюда и название третьей степени — «куб»), d — диагональ
S = 6a 2 d 2 =3a 2
Число граней – 6, форма граней – квадраты, число ребер – 12, число вершин – 8.
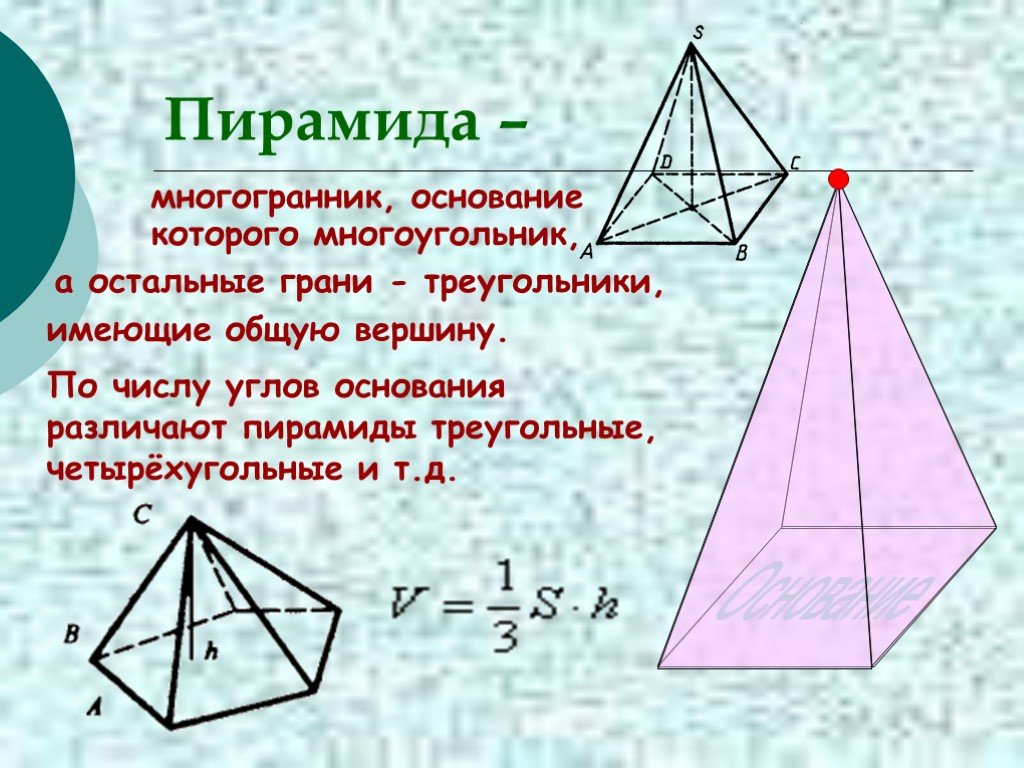
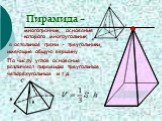
Слайд 26Пирамида –
многогранник, основание которого многоугольник,
а остальные грани - треугольники,
имеющие общую вершину.
По числу углов основания различают пирамиды треугольные, четырёхугольные и т.д.
Основание
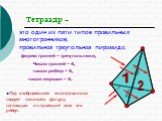
Слайд 274 3 Тетраэдр –
это один из пяти типов правильных многогранников; правильная треугольная пирамида;
1 2 число вершин – 4.
Под изображением многогранника следует понимать фигуру, состоящую из проекций всех его рёбер.
Число граней – 4,
форма граней – треугольники,
число ребер – 6,
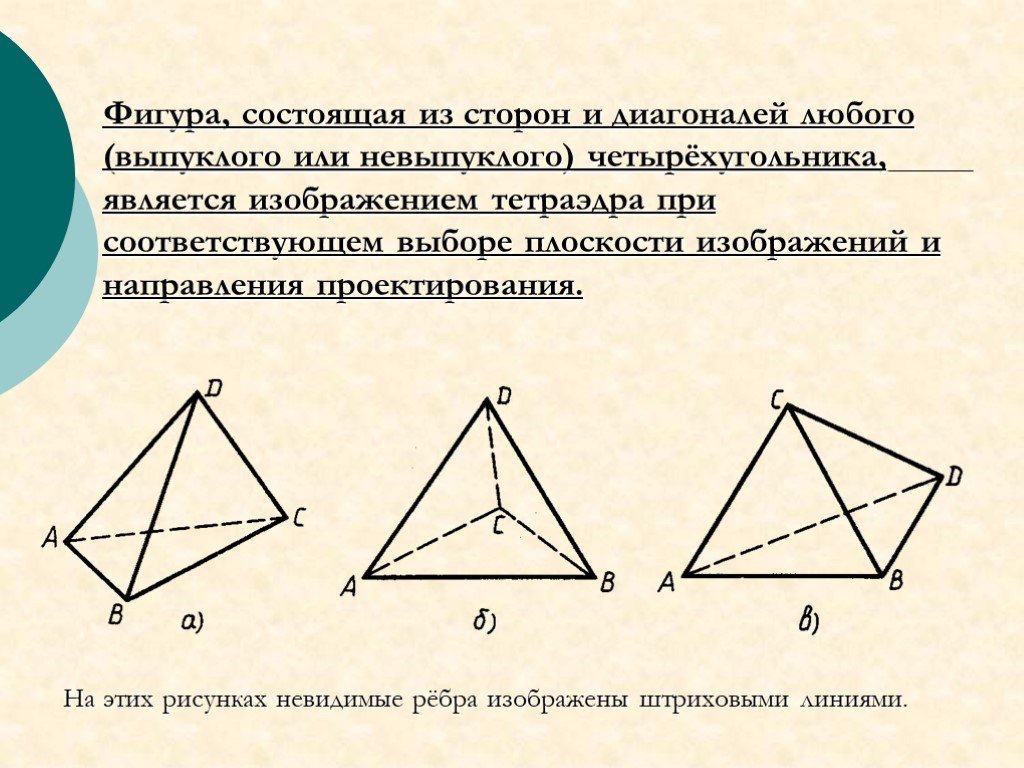
Слайд 28Фигура, состоящая из сторон и диагоналей любого (выпуклого или невыпуклого) четырёхугольника, является изображением тетраэдра при соответствующем выборе плоскости изображений и направления проектирования.
На этих рисунках невидимые рёбра изображены штриховыми линиями.
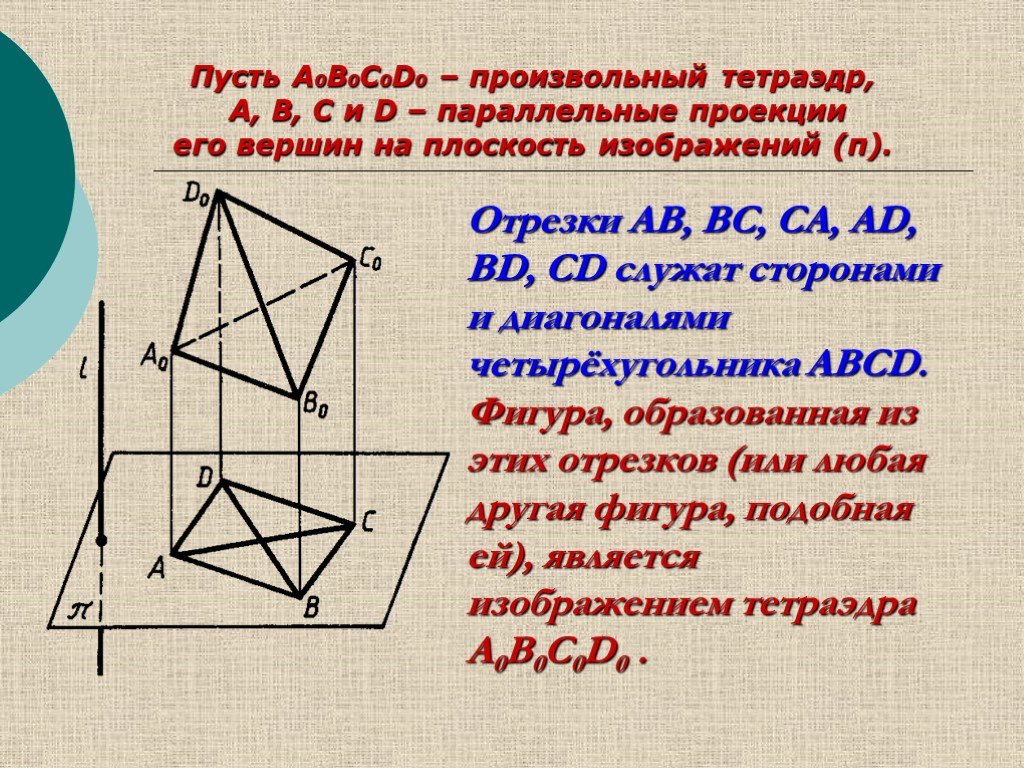
Слайд 29Отрезки AB, BC, CA, AD, BD, CD служат сторонами и диагоналями четырёхугольника ABCD. Фигура, образованная из этих отрезков (или любая другая фигура, подобная ей), является изображением тетраэдра A0B0C0D0 .
Пусть A0B0C0D0 – произвольный тетраэдр, A, B, C и D – параллельные проекции его вершин на плоскость изображений (π).
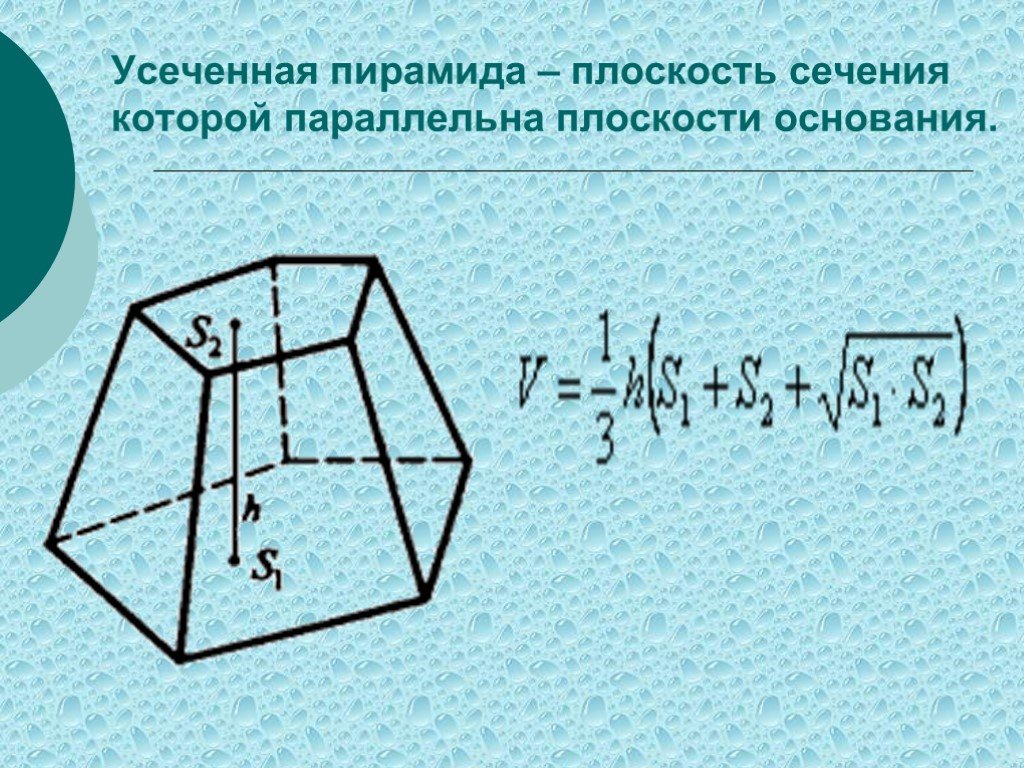
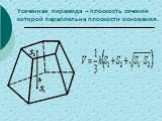
Слайд 30Усеченная пирамида – плоскость сечения которой параллельна плоскости основания.
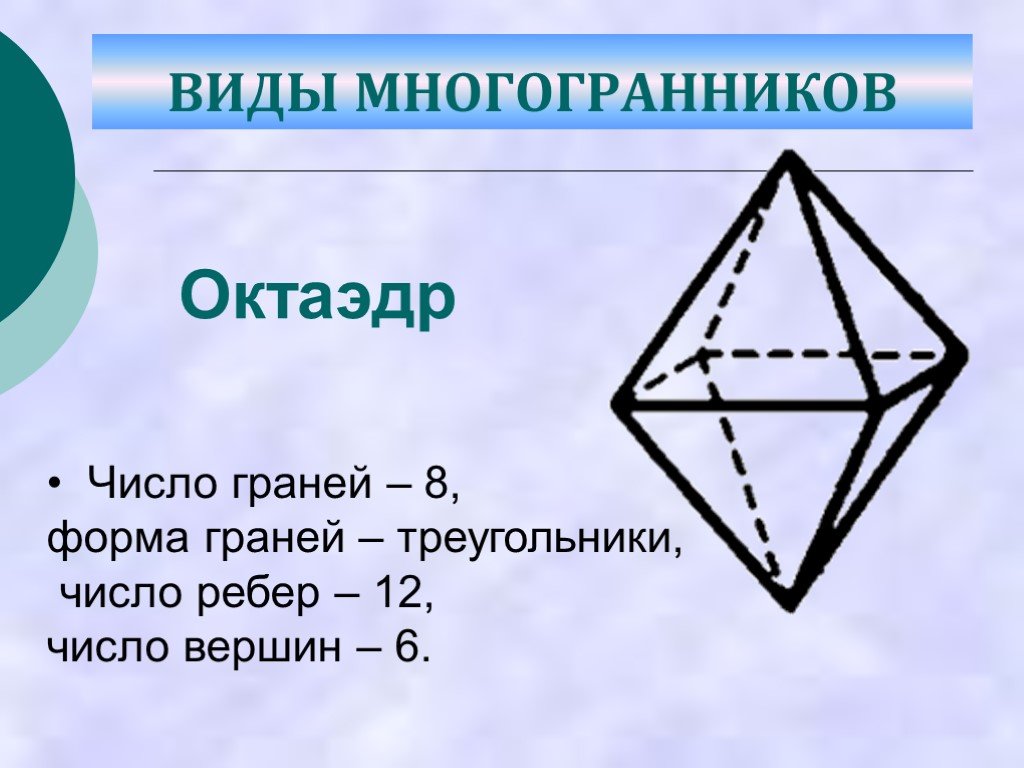
Слайд 31• Число граней – 8, форма граней – треугольники, число ребер – 12, число вершин – 6.
Октаэдр
ВИДЫ МНОГОГРАННИКОВ
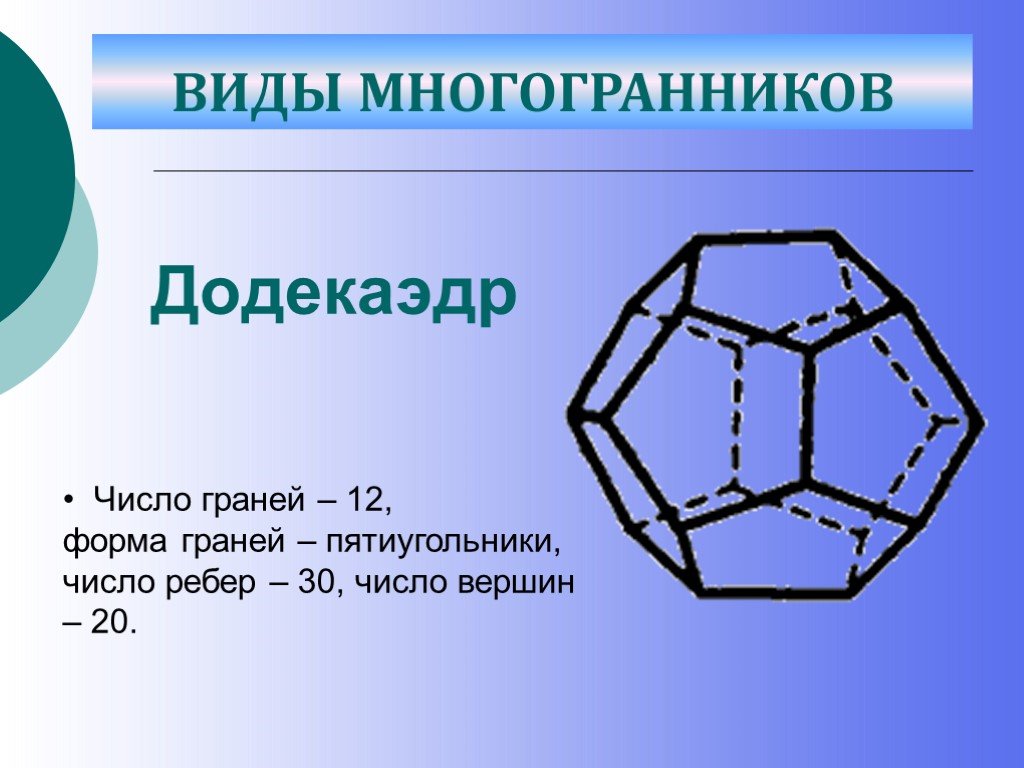
Слайд 32Додекаэдр
• Число граней – 12, форма граней – пятиугольники, число ребер – 30, число вершин – 20.
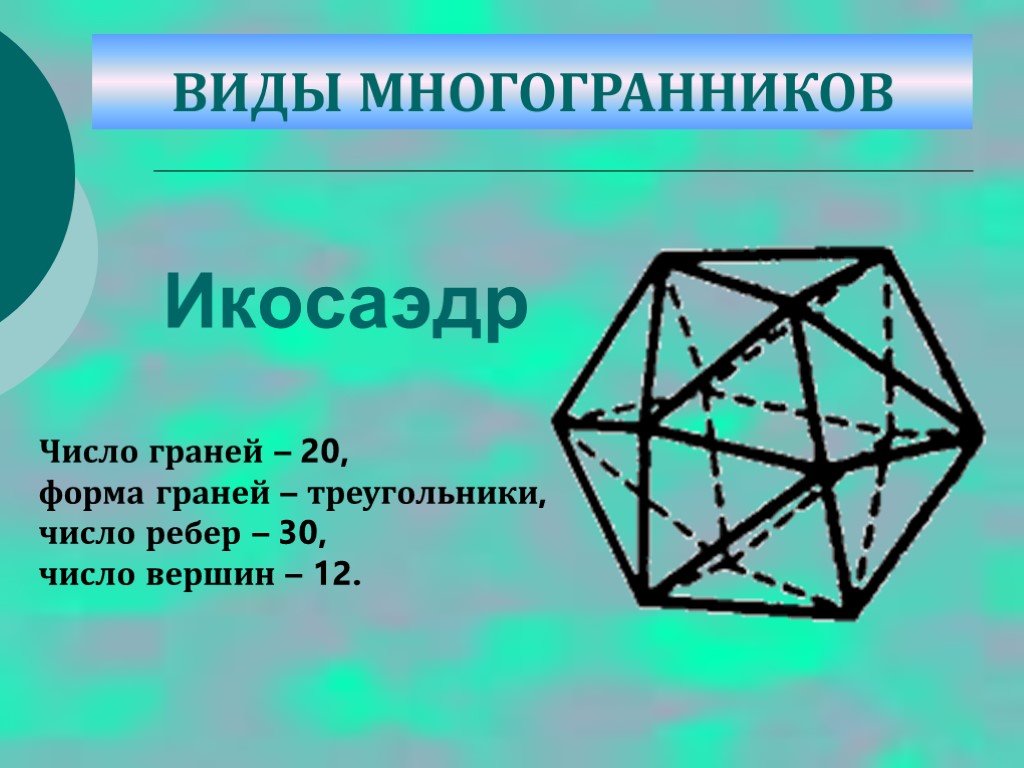
Слайд 33Икосаэдр
Число граней – 20, форма граней – треугольники, число ребер – 30, число вершин – 12.
Слайд 34Цилиндры.
• Круглый прямой. • Круглый усеченный S – площадь боковой поверхности. V – объем.
ТЕЛА ВРАЩЕНИЯ
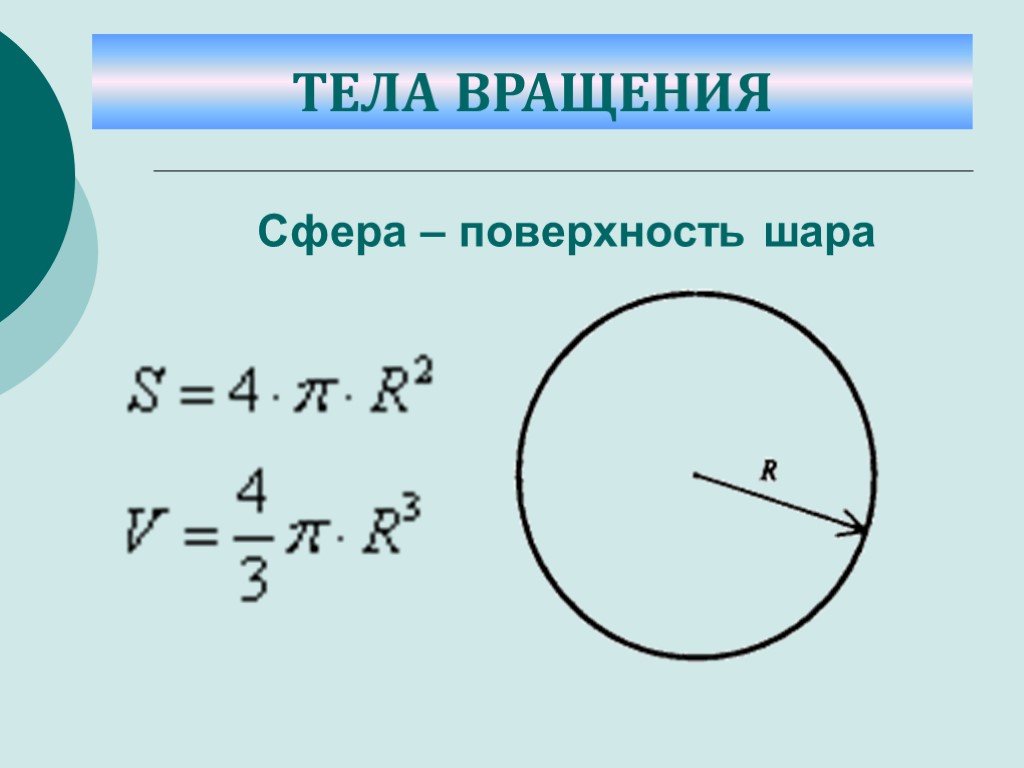
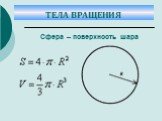
Слайд 35Сфера – поверхность шара
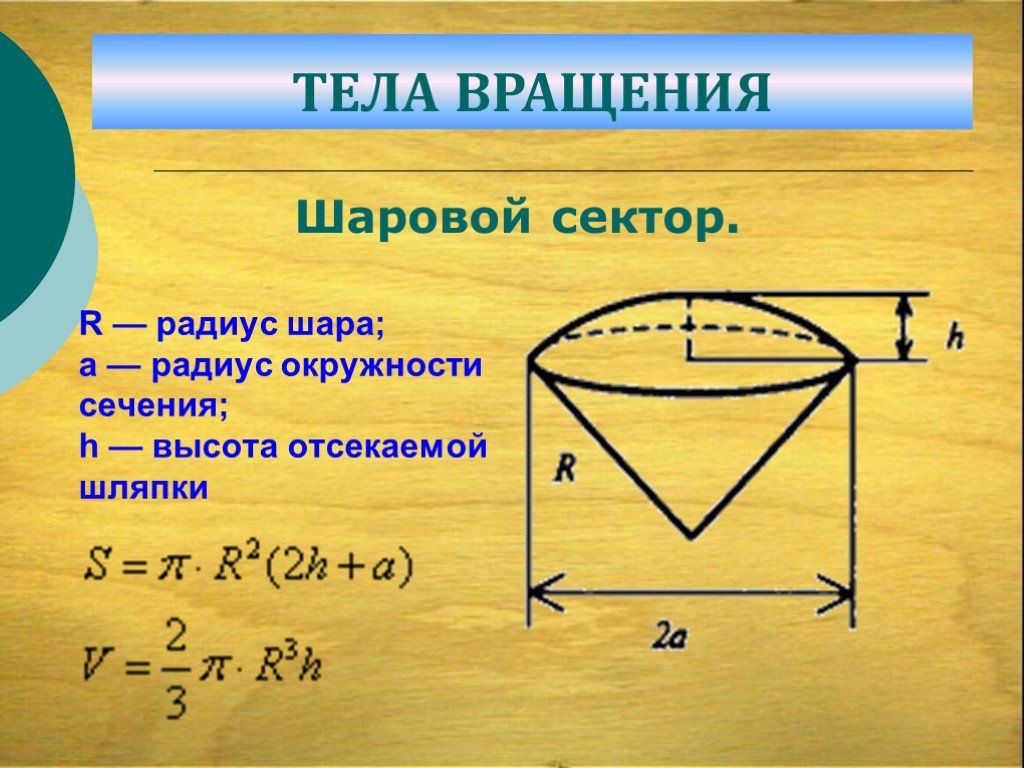
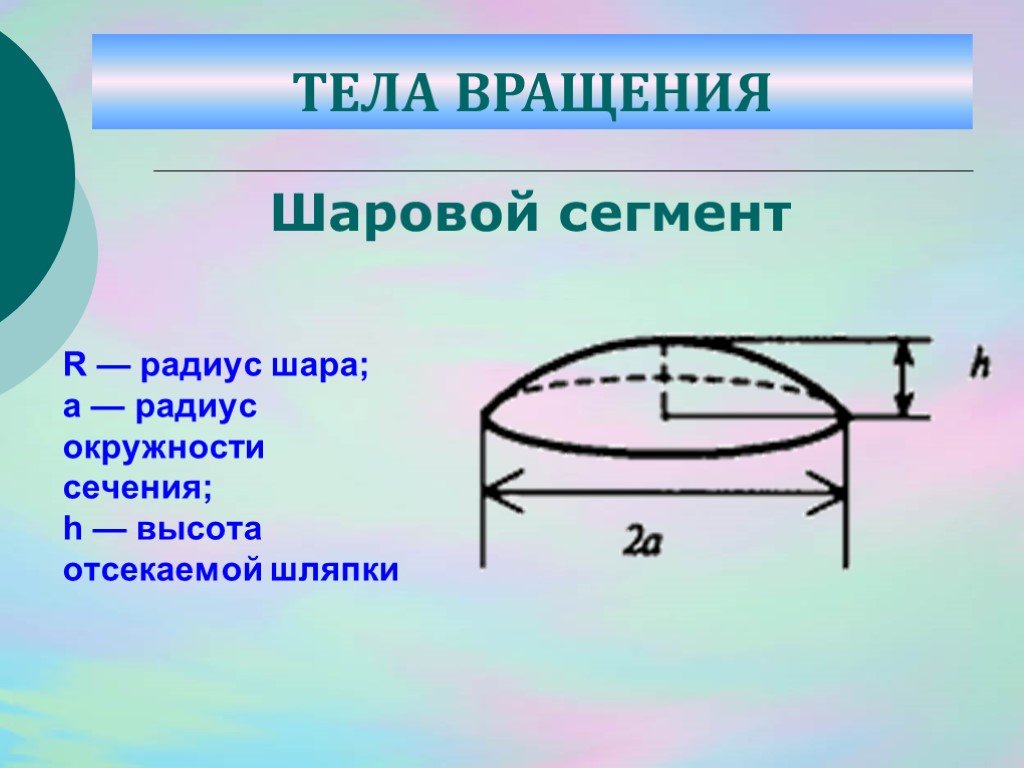
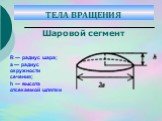
Слайд 36R — радиус шара; а — радиус окружности сечения; h — высота отсекаемой шляпки
Шаровой сектор.
Слайд 38R — радиус шара, a , b — радиусы окружностей сечений, h — высота слоя
Шаровой слой
Слайд 39Сюда входит: выбор оптимального положения изображаемого тела (в частности, выбор ориентации - верх и низ, право и лево), выбор ракурса и проекции, умение минимизировать количество изображенных линий (напомним, что видимые и невидимые линии должны изображаться различным образом), умение строить сечения и проекции на плоскость, умение выделить на пространственном чертеже и соответственно изобразить плоскую конфигурацию, дающую ключ к решению задачи, умение перевести условие задачи на графический язык.
При решении стереометрических задач высоки требования к качеству чертежа, его наглядности.
Нельзя научиться решать сколько-нибудь содержательные стереометрические задачи, не освоив принципы и технику построения пространственного чертежа.
Слайд 40