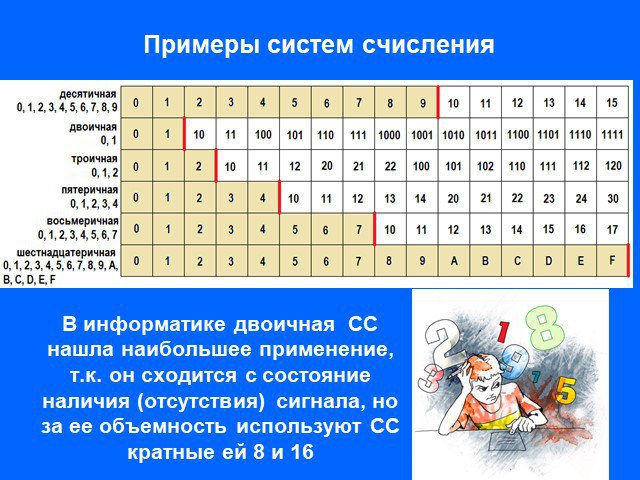
Презентация "Осваиваем перевод из одной системы счисления в другую" по информатике – проект, доклад
Презентацию на тему "Осваиваем перевод из одной системы счисления в другую" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
Информация и информационные процессы. Измерение информации. Системы счисления
Задание № 1. Что из ниже перечисленного не является для вас информацией? а) LIRO CAS. в) Лед – твердое вещество. г) 25 · 15 = 360. б) Сегодня на улице ...Двоичная система счисления. Перевод из двоичной с.с в десятичную
Поставьте соответствия І вариант. Поставьте соответствия ІІ вариант. «ЛОМАЕМ» голову Прочитайте стихотворение А.Н.Старикова:. Ей было 1100 лет, Она ...Автоматизированные и автоматические системы управления
Что такое АСУ и САУ. Компьютеры помогают решать задачи управления в самых разных масштабах: от у правления станком или транспортным средством до управления ...Автоматизированные системы управления технологическими процессами для нефтяной отрасли
Автоматизированная система управления технологическими процессами — совокупность аппаратно-программных средств, осуществляющих контроль и управление ...Логическая организация файловой системы
Для того чтобы предоставить пользователю удобный интерфейс при работе с данными, хранящимися на дисках, ОС подменяет физическую структуру хранящихся ...Компьютерные системы счисления
Проверка домашней работы:. РТ. № 41 (визуально) № 55(3), 56(3)( у доски) №46(устно). По 1 баллу. Где применяется двоичная система счисления? Каков ...Компьютерные словари и системы машинного перевода текстов
Компьютерные словари. Компьютерные словари могут содержать переводы на разные языки сотен тысяч слов и словосочетаний, а также предоставляют пользователю ...Информация в памяти компьютера. Системы счисления
Как представлена информация в компьютере? Информация в компьютере представлена двумя цифрами 0 и 1. Системы счисления. Позиционные Непозиционные. ...История чисел и систем счисления
Система счисления - это. Числа: 1956, 1000073, LXC Цифры: 4, 2, 8, L, C, X Алфавит – это набор цифр. Способ записи чисел с помощью специальных знаков ...Информационные системы и базы данных
Элементарные понятия о данных. Данные – это сведения о чем –либо, которые хранятся в базе, но не используются. Информация – сведения, которые используются. ...Информационные системы
Информационные системы. Информационная система (ИС) — это система, построенная на базе компьютерной техники, предназначенная для хранения, поиска, ...UNIX И UNIX-подобные системы
История UNIX и Linux. ОС UNIX появилась в конце 60-х годов как операционная система для мини-ЭВМ PDP-7. Активное участие в разработке приняли Кеннет ...Операционные системы
Ядро ОС. Ядро ОС – совокупность управляющих программ, которые должны постоянно присутствовать в ОП и обеспечивать функционирование с минимальными ...Корпоративные информационные системы
План. О КИС Интегрированная информационная среда Методы интеграции. КИС как составляющая современной инфраструктуры организации. Корпоративная информационная ...Вычислительные системы
Вычислительная система (ВС) - это взаимосвязанная совокупность аппаратных средств вычислительной техники и программного обеспечения, предназначенная ...Возможности операционной системы Linux в учебном процессе Возможности операционной системы Linux в учебном процессе
Цель и задачи. Цель: Исследовать возможности операционной системы Линукс в сравнении с Windows помочь школьнику разобраться с интерфейсом операционной ...Возможности операционной системы Linux
Цель:. Расширить представление о возможностях использования ОС «Линукс» в образовательном процессе. Задачи:. Ознакомить с основами работы в офисном ...Возможности операционной системы Linux в учебном процессе
Цель и задачи. Цель: Исследовать возможности операционной системы Линукс в сравнении с Windows помочь школьнику разобраться с интерфейсом операционной ...Воздушные системы охлаждения
Анализ систем воздушного охлаждения. Работа систем воздушного охлаждения основана на эффекте охлаждения устройств находящихся в воздушном потоке. ...Конспекты
Перевод целых чисел из одной системы счисления в другую
ПЛАН-КОНСПЕКТ УРОКА Перевод целых чисел из одной системы счисления в другую. (Тема урока). . ФИО (полностью). . Спичкова Наталья Викторовна. ...Перевод чисел из одной системы счисления в другую
Тема урока: «Перевод чисел из одной системы счисления в другую». Цель урока:. сформировать у учащихся навыки и умения переводить числа из одной ...Перевод чисел из одной системы счисления в другую
Тема урока:. «Перевод чисел из одной системы счисления в другую», 8 класс, информатика. Цели урока:. . - Научить, учащихся переводить числа. из ...Системы счисления. Перевод чисел из одной системы в другую
ИНФОРМАТИКА 1 курсы 1 семестр. Раздел «Информация» Системы счисления. ______________________________________________________________________________________________________. ...Непозиционные и позиционные системы счисления. Перевод чисел из одной системы счисления в другую. 8 класс
Тема. Непозиционные и позиционные системы счисления. Перевод чисел из одной системы счисления в другую. 8 класс. Цель. :. . Образовательные:. ...Двоичная арифметика. Перевод чисел из одной системы счисления в другой
Урок по информатике - с. истемы счисления:. Двоичная арифметика. Перевод чисел из одной системы счисления в другой. Цели урока:. . Обучающая. ...Перевод чисел из десятичной системы счисления в любую другую
ПЛАН-КОНСПЕКТ УРОКА. «Перевод чисел из десятичной системы счисления в любую другую». . ФИО (полностью). . Помыкалова Елена Викторовна. ...Перевод из десятичной системы счисления в двоичную и обратно
Конспект урока информатики в 6 классе по теме. «Перевод из десятичной системы счисления в двоичную и обратно». Подготовил: учитель ...Перевод их одной системы в другую
Тема: Перевод их одной системы в другую. Цель урока:. Образовательная: познакомить учащихся с понятием и научить учащихся переводить из одной ...Перевод чисел из десятичной системы счисления в восьмеричную, шестнадцатеричную систему счисления
Государственное учреждение. «ОТДЕЛ ОБРАЗОВАНИЯ ГОРОДА КОСТАНАЯ». Школа – лицей №1. Конспект урока по информатике в 8 классе«Перевод ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:22 октября 2016
Категория:Информатика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию