Презентация "Графы. Поиск путей в графе" по информатике – проект, доклад
Презентацию на тему "Графы. Поиск путей в графе" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Поиск информации в Интернете
Для поиска информации используются специальные поисковые системы, которые содержат постоянно обновляемую информацию о местонахождении Web-страниц ...Поиск информации в сети Интернет
Поисковые системы. Для поиска информации в сети Интернет существуют поисковые системы, которые содержат информацию о ресурсах Интернета. Каждая поисковая ...Поиск информации в Интернете
Цель занятия: ознакомиться с различными типами поисковых систем, научиться находить необходимую информацию в Интернете. ИПС- информационно-поисковые ...Поиск информации в интернете
Это самый быстрый способ поиска, но его можно использовать только в том случае, если точно известен адрес документа или сайта, где расположен документ. ...Поиск информации в интернете
Не теряйте время. Чтобы правильно и быстро организовать поиск информации необходимо: Определить конкретную тему, Использовать гиперссылки, относящиеся ...Поиск информации в Интернете
Поиск информации в Интернете. Для поиска информации в Интернете используются специальные поисковые серверы, которые содержат в базах данных постоянно ...Поиск информации в Internet
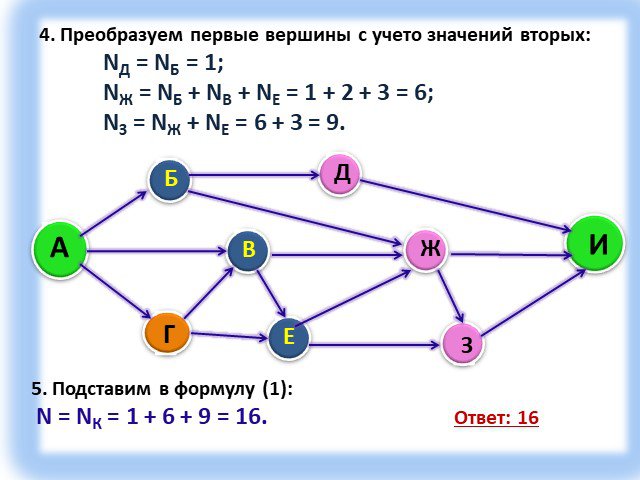
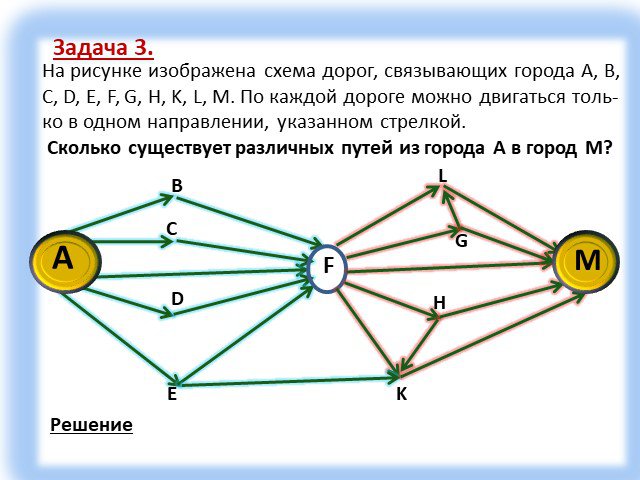
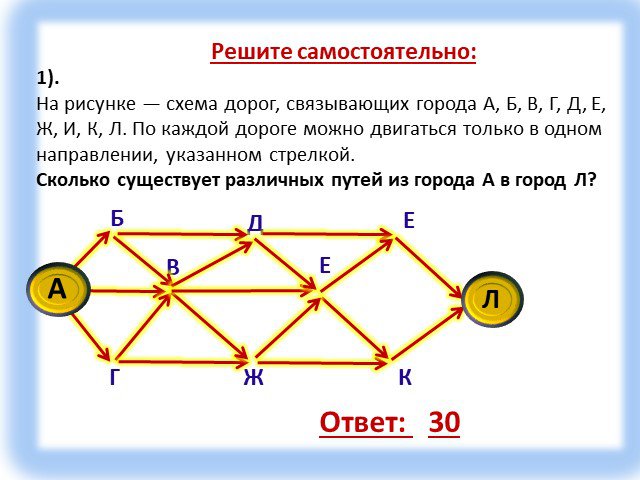
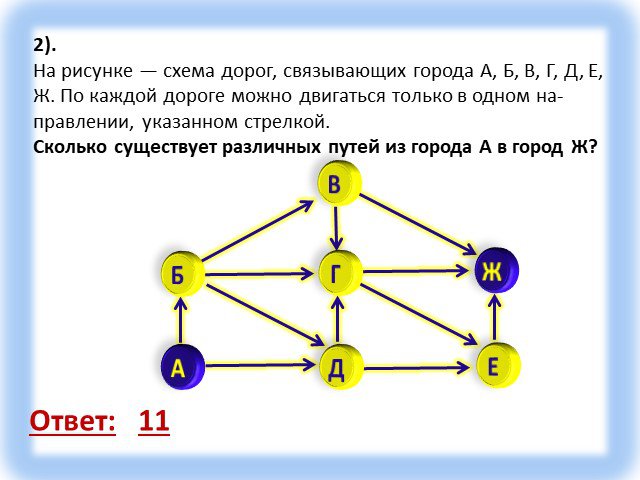
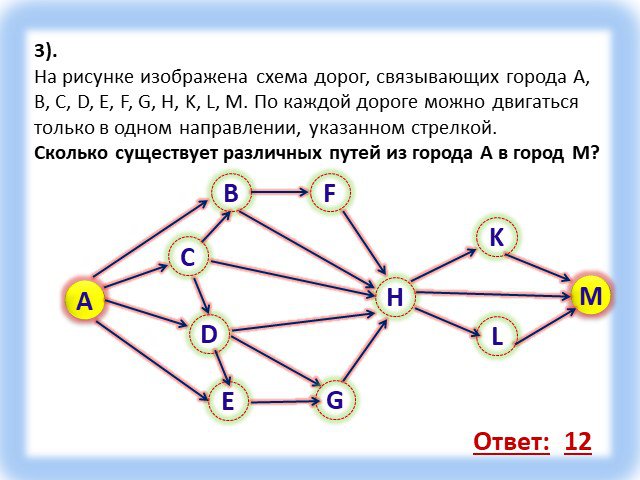
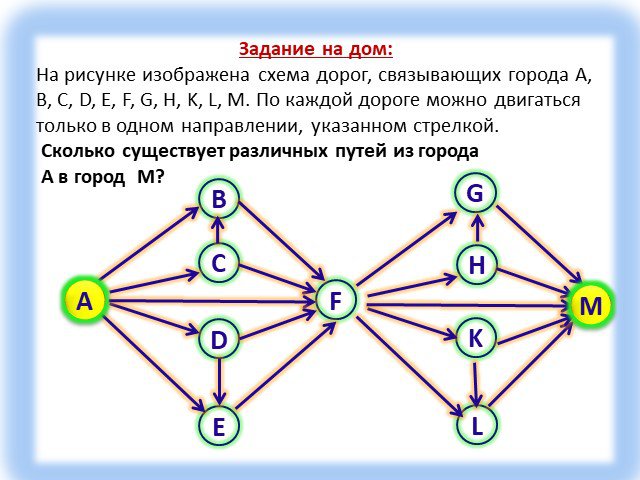
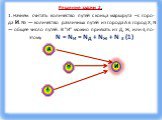
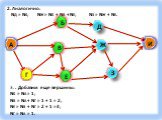
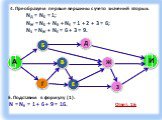
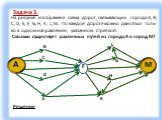
Тип урока: Урок актуализации ранее полученных знаний, с применением современных компьютерных технологий. Форма урока: урок-зачет. Технология: личностно-ориентированная, ...Графы
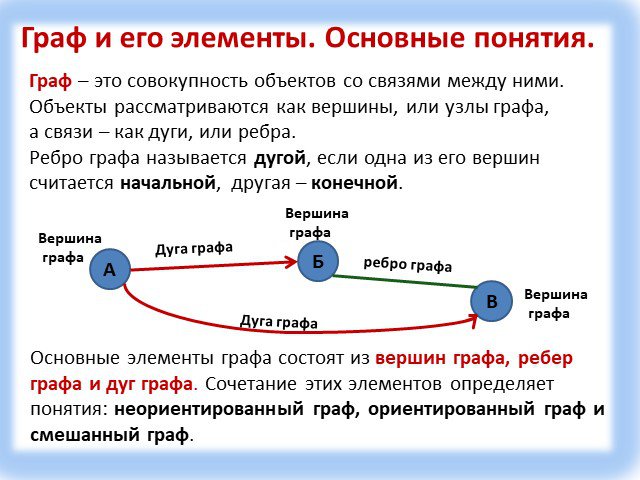
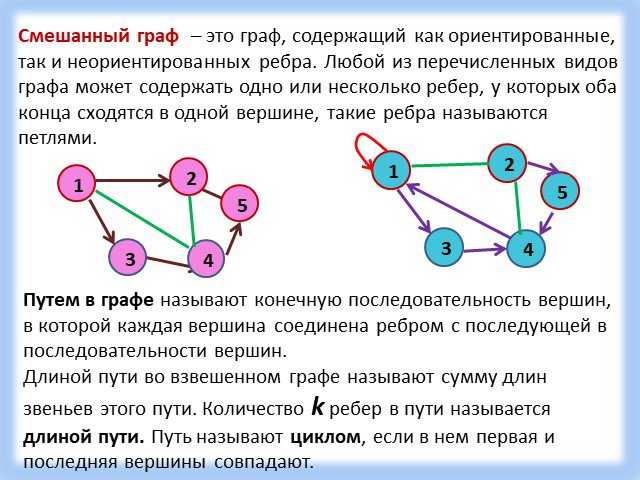
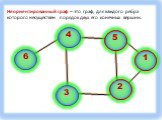
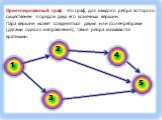
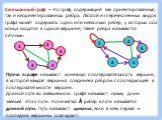
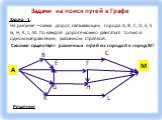
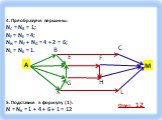
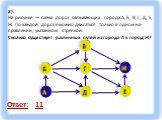
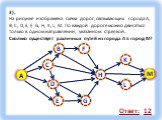
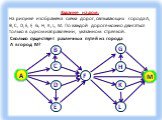
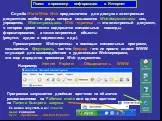
Граф – это конечная совокупность вершин, некоторые из которых соединены ребрами т.е. это совокупность точек, называемых вершинами, и линий, соединяющих ...Поиск и сортировка информации в базах данных
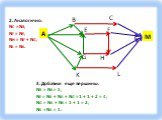
Задача № 1. Результаты тестирования представлены в таблице:. Сколько записей в ней удовлетворяют условию «Пол =’ж’ ИЛИ Химия > Биология»? Решение. ...Поиск информации
Алгоритмы поиска информации. Линейный поиск. Пример:. Написать программу поиска элемента х в массиве из n элементов. Значение элемента х вводится ...Поиск и просмотр информации в Интернет
Просмотр информации в Интернет. В момент запуска Обозреватель загружает титульную Web – страницу. Пользователь может сам назначить эту страницу. Для ...Поиск и замена данных. Сортировка, фильтрация данных. Отчеты
1. В какой вкладке находится значок «Конструктор таблиц» ? а) Создание б) Режим таблицы с) Главная. 2. В какой вкладке находится значок «режим»? а) ...Поиск в интернете
Это самый быстрый способ поиска, но его можно использовать только в том случае, если точно известен адрес документа или сайта, где расположен документ. ...Поиск информации в сети Интернет
Веб – сервер - это компьютер, на котором установлено специальное программное обеспечение. Веб – сайт - это место на веб - сервере. В сети Интернет ...Поиск информации в глобальной сети
Глобальная сеть интернет. Поиск информации в глобальной сети. Статистика использования интернета в 2014. Интернет - это глобальная сеть компьютерных ...Поиск файлов и папок
Автор - Флеонов В.В. Для поиска файлов и папок используется: Главное меню «Пуск» / «Поиск» и/или кнопка «Поиск» на панели в открытом окне. . Для поиска ...Алгоритмы на графах: определение наличия циклов в графе
Домашнее задание. Какое максимальное количество рёбер может быть в ориентированном ациклическом графе с n вершинами? Может ли быть так, что правильным ...Конспекты
Поиск информации в сети Интернет
Конспект урока. Предмет информатика. Класс 9. . . Тема урока: «Поиск информации в сети Интернет». Цель:. формирование навыков поиска ...Поиск информации в сети Интернет. Сетевое взаимодействие
Открытый урок по информатике в 8 классе. 31.01.2014 г. Тема: «Поиск информации в сети Интернет. Сетевое взаимодействие». Учитель: Конякина Т.В. ...Поиск информации в Интернете
План-конспект урока информатики по теме:. . «Поиск информации в Интернете». для учащихся 11 класса. учителя информатики и ИКТ. . муниципального ...Поиск информации в сети Интернет
Автор: Пастлер Елена Эдуардовна. Место работы: МОУ «Школа №71» г. Прокопьевска Кемеровской области. Должность: учитель информатики. Урок информатики ...Возможности Интернета. Поиск информации в сети Интернет
Урок №33. Тема: Возможности Интернета. Поиск информации в сети Интернет. Цель:. Актуализировать знания учащихся о глобальной сети Интернет. Дать ...Поиск информации в Интернете
Тема: «. Поиск информации в Интернете. ».Цели урока:. 1. Познакомить учащихся со способами поиска информации. 2. Рассказать о поисковых системах, ...Поиск информации в Интернет
МБОУ СОШ с углубленным изучением информатики № 68 г. Пензы. Аверина А.М., учитель информатики первой кв. категории. . Открытый урок по информатике. ...Поиск максимального элемента массива
Урок на тему «Поиск максимального элемента массива». Откройте программу Lazarus. и создайте новый проект (Проект / создать / приложение). . ...Интернет. Поиск информации в интернете. Электронная почта
Дата:. Класс: 6. Тема: Интернет. Поиск информации в интернете. Электронная почта. Цель:. Общеобразовательные:. учащиеся должны освоить основные ...Поиск информации
Технологическая карта урока. Босова Л.Л. Информатика . 5 класс. ФГОС. Урок 24. Поиск информации. . . Планируемые образовательные результаты:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Информатика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию