Презентация "Анализ собственных колебаний в MSC" по информатике – проект, доклад
Презентацию на тему "Анализ собственных колебаний в MSC" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 32 слайд(ов).
Слайды презентации
Список похожих презентаций
Редуцирование в динамическом анализе в MSC
Раздел 4. Редуцирование в динамическом анализе. ВВЕДЕНИЕ В ДИНАМИЧЕСКОЕ РЕДУЦИРОВАНИЕ………………………………….… 4 - 3 МЕТОДЫ ДИНАМИЧЕСКОГО РЕДУЦИРОВАНИЯ В MSC.Nastran…………………… ...Компьютерные технологии инженерного анализа MSC
Стр. Цель семинара 3 Коротко о компании 4 Что такое MSC Nastran 6 Поддержка клиентов MSC 9 Дополнительные источники информации 11 Обучение в MSC.Software ...Анализ отклика на случайное воздействие в MSC
Раздел 14. Анализ отклика на случайное воздействие. ТИПЫ ДИНАМИЧЕСКИХ ПРОЦЕССОВ………………………………… 14 - 4 АНАЛИЗ ОТКЛИКА НА СЛУЧАЙНОЕ ВОЗДЕЙСТВИЕ..……...…….. ...Бездеформационные методы колебаний в MSC
Раздел 5. Бездеформационные моды колебаний. БЕЗДЕФОРМАЦИОННЫЕ МОДЫ И ВЕКТОРЫ. АСПЕКТЫ ТЕОРИИ……………… 5 - 3 ВЫЧИСЛЕНИЕ БЕЗДЕФОРМАЦИОННЫХ МОД.………………………………………. ...Анализ долговечности при помощи MSC.Fatigue
DISCLAIMER MSC.Software Corporation reserves the right to make changes in specifications and other information contained in this document without ...Динамический анализ в MSC
Corporate MSC.Software Corporation 815 Colorado Boulevard Los Angeles, CA 90041-1777 Telephone: (323) 258-9111 or (800) 336-4858 FAX: (323) 259-3638 ...Шпаргалка по командам Unix в MSC
Шпаргалка по командам Unix. Шпаргалка по командам Unix (продолжение). . ...Анализ интернет-ресурсов для подготовки школьников к экзаменам
На вопрос «Вы используете (будете использовать) Интернет для подготовки к экзамену?» из 43 обучающихся 9-х классов 41 человек ответили положительно. ...Расчет статической аэроупругости в MSC
Цель. Целью расчета статической аэроупругости является определение нагрузок на ЛА при стационарном или квазистационарном маневре. Маенвр описывается ...Расчет антисимметричного летательного аппарата в MSC
Описание конструкции ЛА. Размах крыла: 12 м Хорда: 2 м Передняя кромка крыла: на расстоянии 0.3 м от точки отсчета Носок: на расстоянии 2 м от точки ...Программный датчик деформаций MSC
ИНСТРУМЕНТ ДЛЯ ПРОВЕДЕНИЯ ВИРТУАЛЬНОГО ТЕСТА В СРЕДЕ MSC.Fatigue. ПРОГРАММНЫЙ ДАЧТИК ДЕФОРМАЦИЙ. Конечно-элементный инструмент, позволяющий создать ...Построение системы управления информацией о материалах в MSC
Построение системы информационного управления материалами. Во-первых необходимо определить потребности конечных пользователей Во-вторых необходимо ...Нахождение материала и печать отчета в MSC
Описание задачи Выполнив упражнение, вы познакомитесь с пользовательским интерфейсом MSC.Mvision Evaluator, используя учебную версию банка данных ...Введение в MSC
MSC.MVISION – база данных, содержащая свойства материалов. Поставщики информации о материалах. Потребители информации о материалах. Контроль соответствия ...Анализ ресурсов по подготовке учащихся к ЕГЭ по информатике
Технопарк в сфере высоких технологий “Жигулёвская долина" областная целевая программа на 2010-2014 годы. Приоритетными направлениями специализации ...Анализ образовательного сайта
Адрес в Интернете: www.scenarist.boom.ru/. Сценарии школьных праздников. В этом сайте есть несколько разделов: Интеллектуальные игры Детский сад Школьные ...Анализ информации представленной в виде схем
Задача:. На схеме нарисованы дороги между четырьмя населёнными пунктами А, В, С, Д и указаны протяжённости данных дорог:. А С Д В 3 6. Определите. ...Метод остаточных векторов в MSC
Раздел 11. Метод остаточных векторов. ИДЕЯ МОДАЛЬНОГО ПОДХОДА..……………………………..……… 11 - 3 СПОСОБЫ КОМПЕНСАЦИИ ОТСУТСТВИЯ МОД………………….... 11 - 5 ОСТАТОЧНЫЙ ...Внешние переменные и элементы NOLIN в MSC
Раздел 17. Внешние переменные, передаточные функции и элементы NOLIN. ВНЕШНИЕ ПЕРЕМЕННЫЕ..………………………………….………………………17 - 3 ПЕРЕДАТОЧНЫЕ ФУНКЦИИ...………………………………………..……………. ...Печать отчета в MSC
Выбрав материал, можно напечатать на принтере отчет. ПЕЧАТЬ ОТЧЕТА. Доступ к печати из Material Browser или Data Viewer Браузер печатает данные в ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:5 марта 2019
Категория:Информатика
Содержит:32 слайд(ов)
Поделись с друзьями:
Скачать презентацию







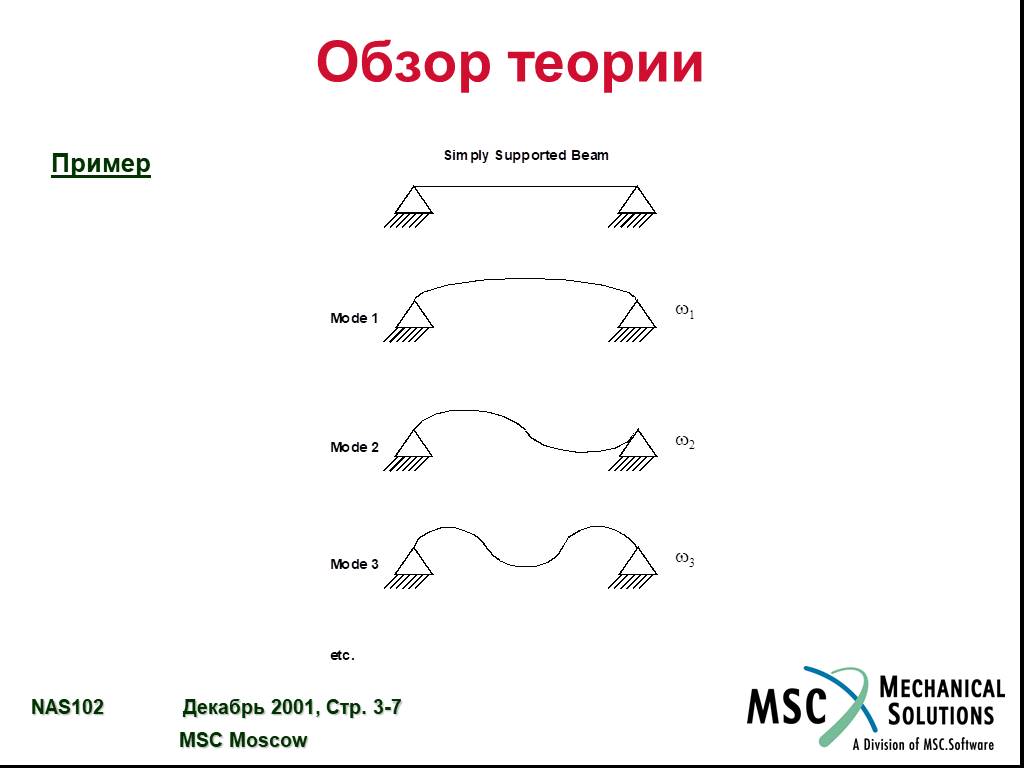

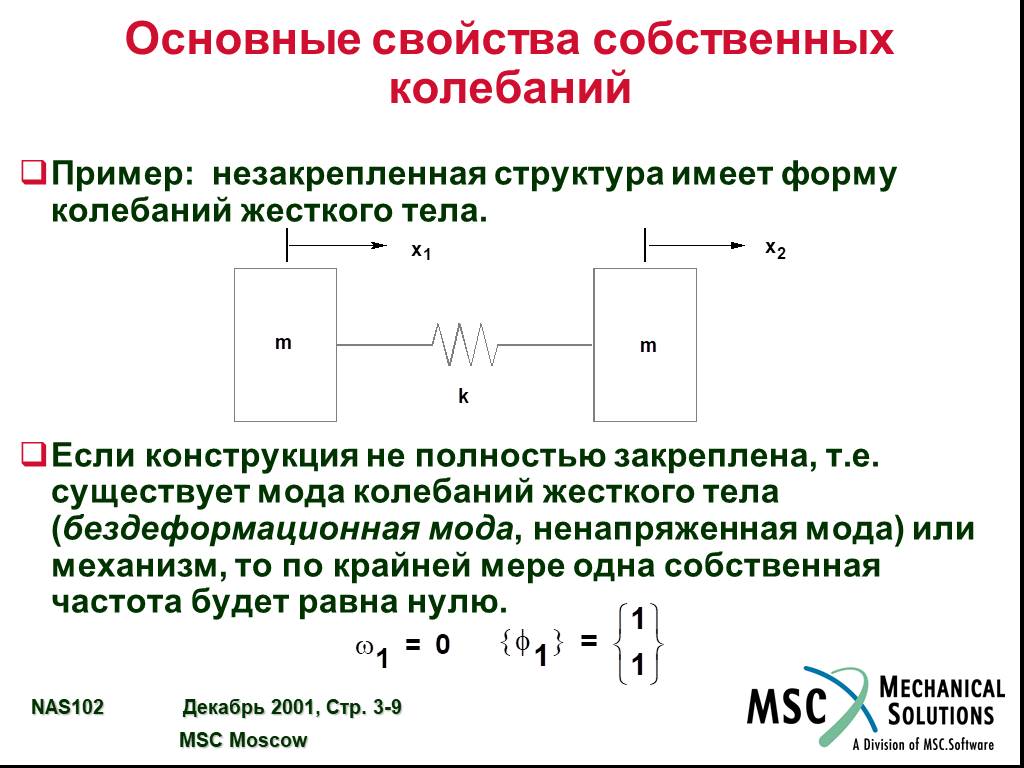
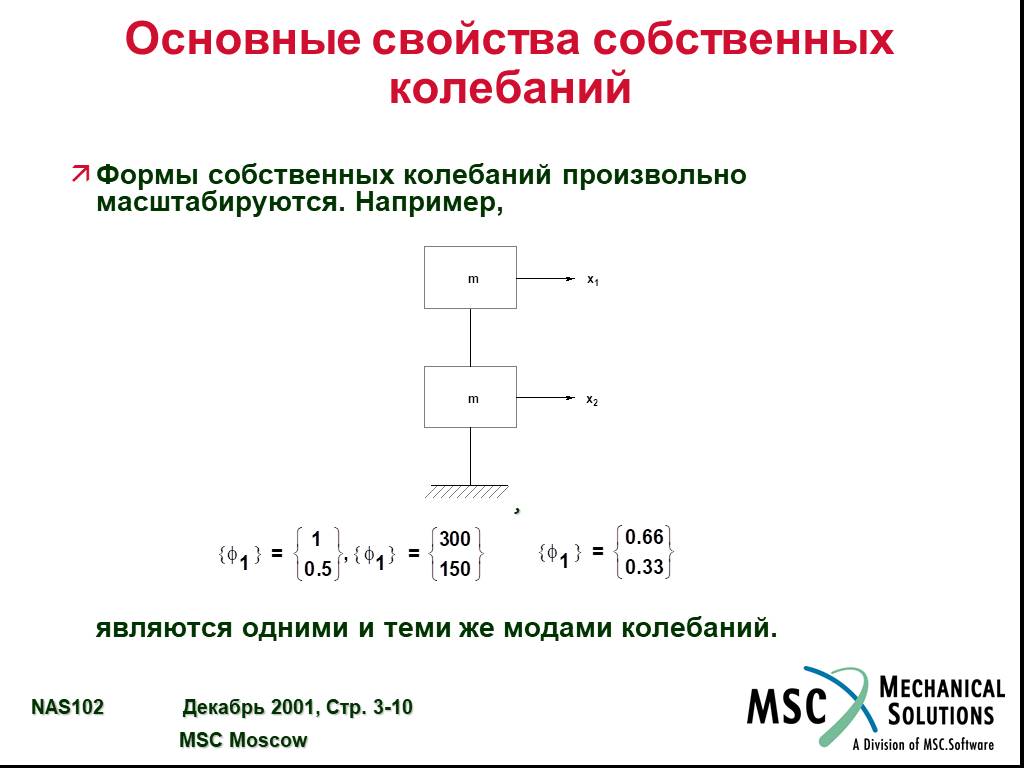













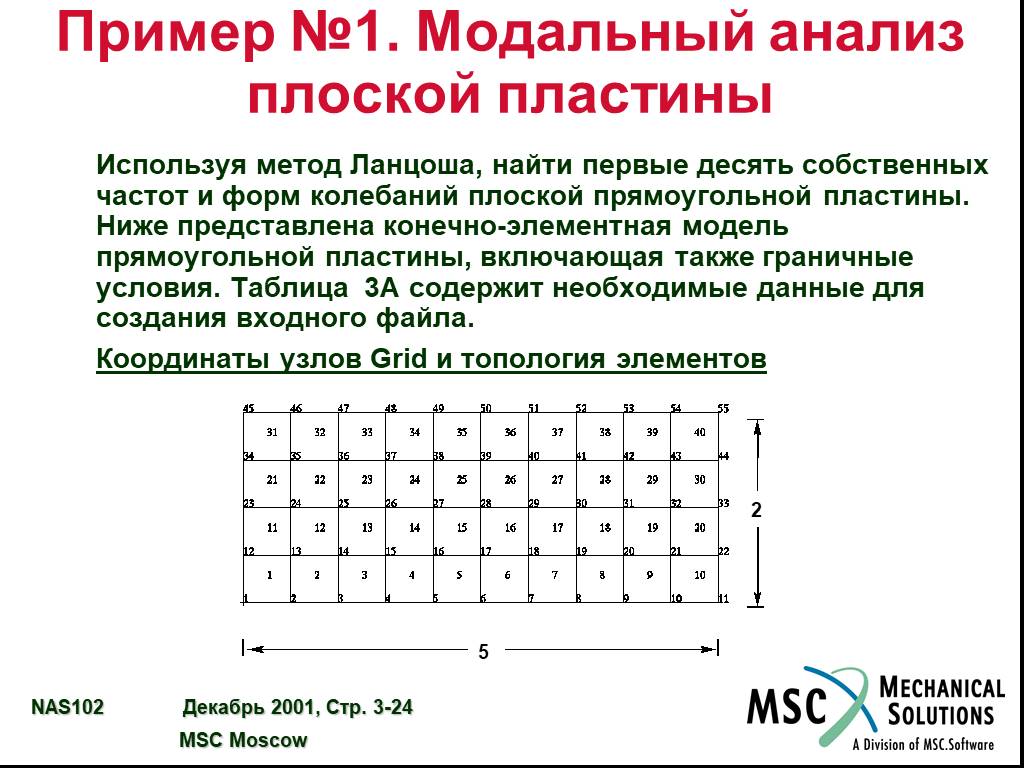















![Основные свойства собственных колебаний. Если [K] и [M] симметричные и действительные (что характерно для конечно-элементных моделей обычных конструкций), справедливы следующие условия ортогональности: и а также Собственные частоты (w1,w2,…) измеряются в рад/c. Для этого можно использовать также Гц Основные свойства собственных колебаний. Если [K] и [M] симметричные и действительные (что характерно для конечно-элементных моделей обычных конструкций), справедливы следующие условия ортогональности: и а также Собственные частоты (w1,w2,…) измеряются в рад/c. Для этого можно использовать также Гц](https://prezentacii.org/upload/cloud/19/03/130588/images/thumbs/screen8.jpg)





















































