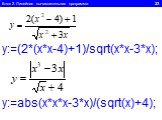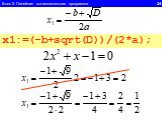Презентация "Линейный алгоритм" по информатике – проект, доклад
Презентацию на тему "Линейный алгоритм" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 44 слайд(ов).
Слайды презентации
Список похожих презентаций
Линейный алгоритм в жизни
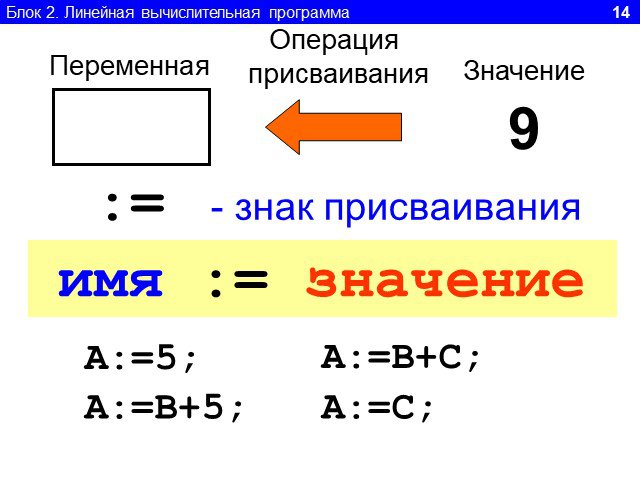
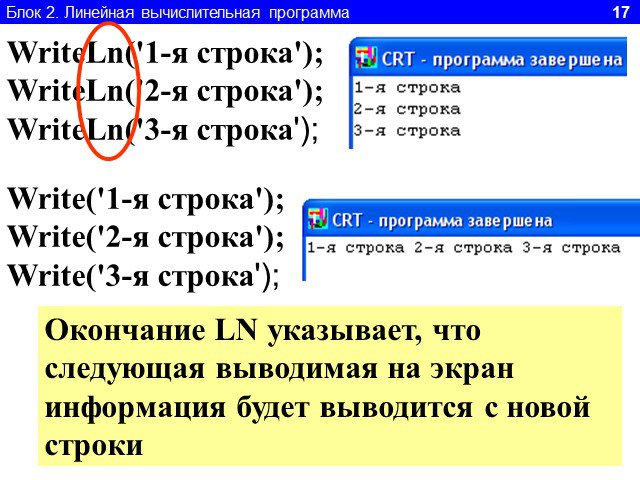
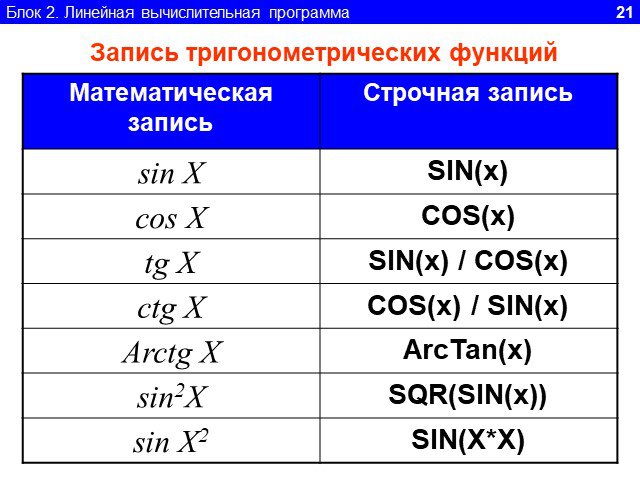
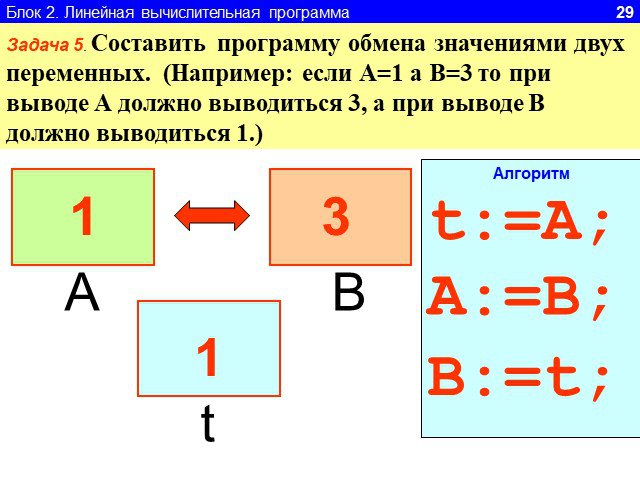
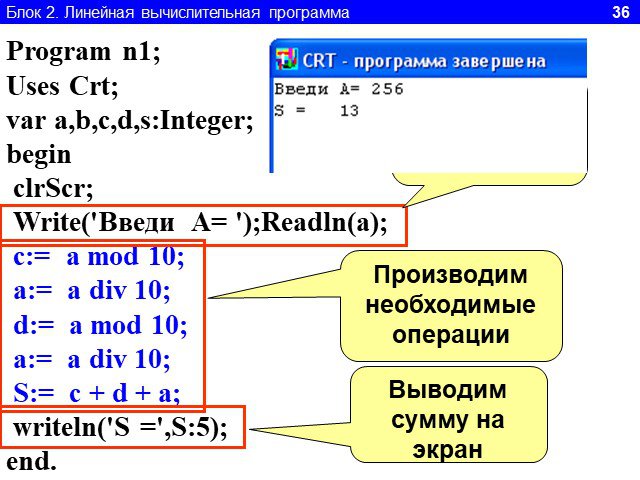
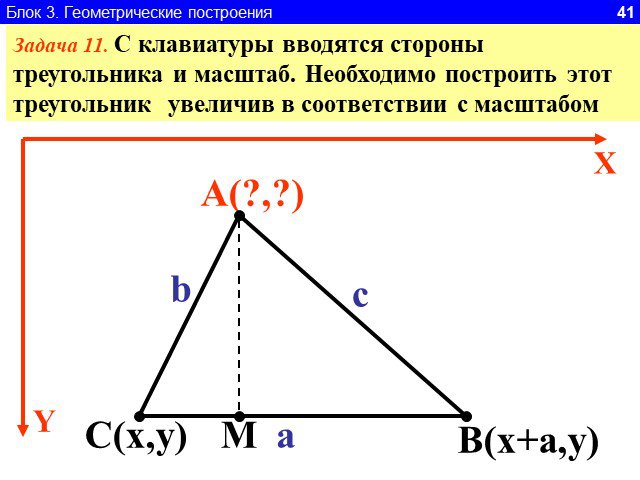
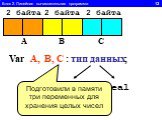
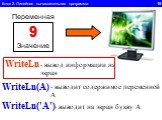
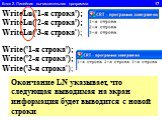
Линейный алгоритм-. это такой алгоритм, который идёт всё время последовательно. Как механизм в часах: после 1,следует 2, после 2-3, после 3-4 должен ...Формы записи алгоритма. Линейный алгоритм
Цель урока:. формирования знаний в области алгоритмов, организация работы по усвоению новых понятий. Что такое алгоритм? Что такое СКИ? Кто является ...Линейный алгоритм
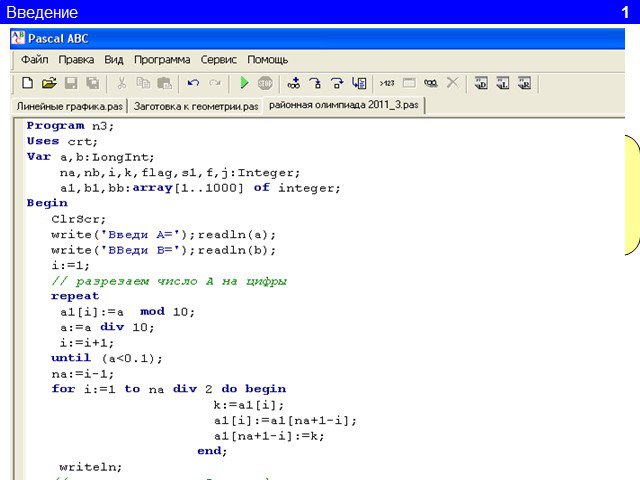
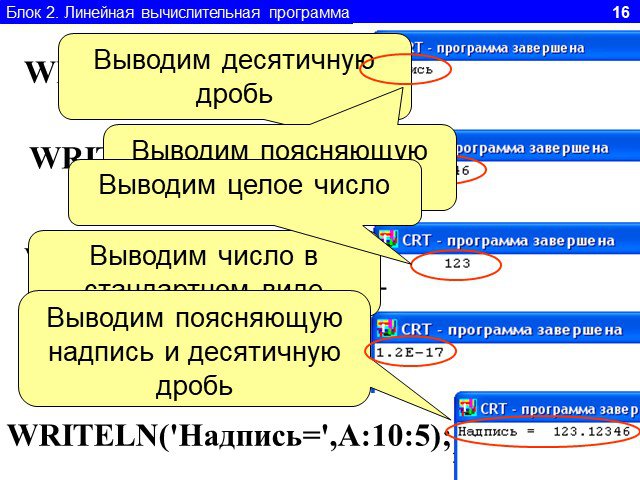
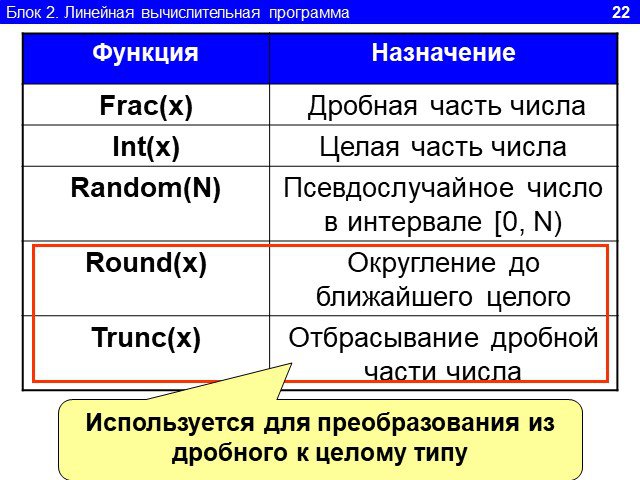
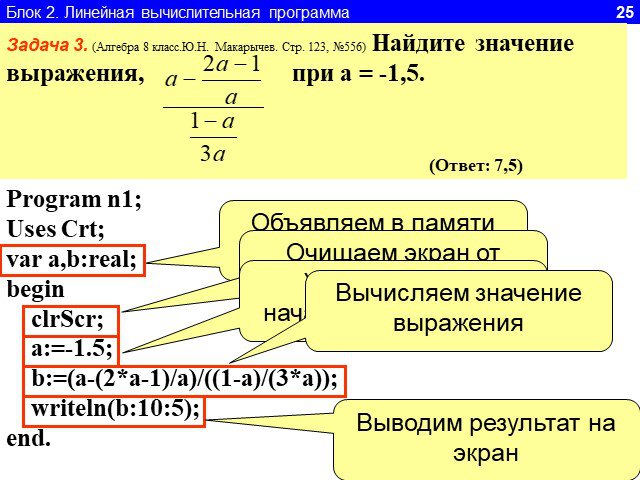
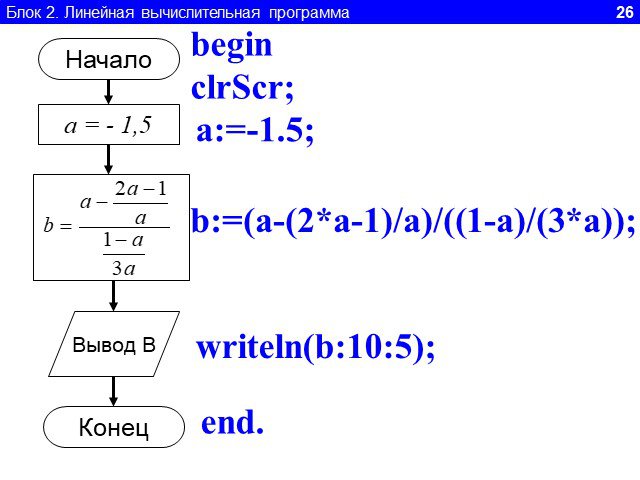
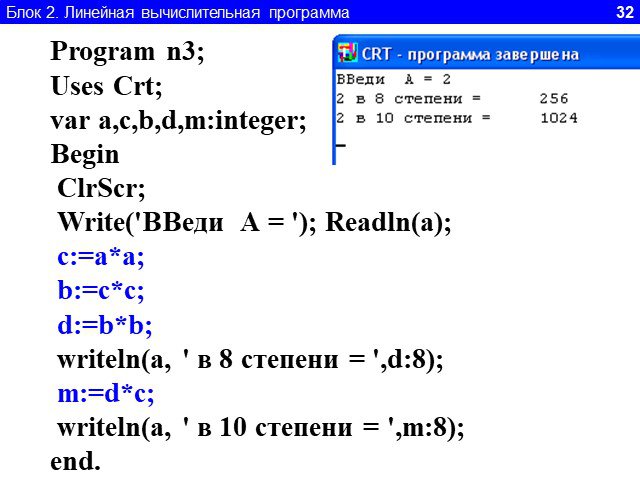
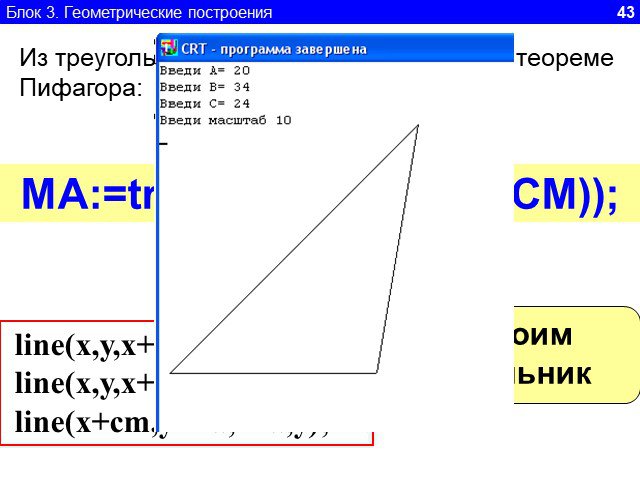
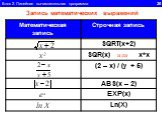
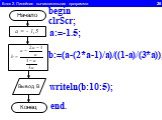
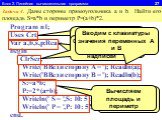
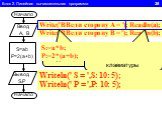
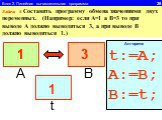
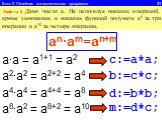
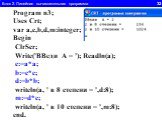
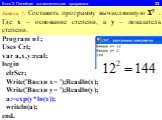
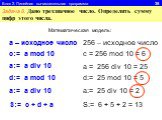
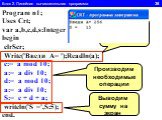
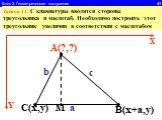
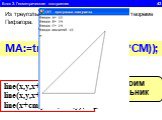
1.Определите значение целочисленной переменной а после выполнения фрагмента алгоритма. а:=247; b:=(a div 100)*10+9; a:=(10*b-a) mod 10; Примечание. ...Линейный алгоритм
Цели урока:. Закрепление понятия «линейный алгоритм». Развитие умений выделять главное, сравнивать, анализировать, проводить аналогию, обобщать, творчески ...Циклический алгоритм
Многие процессы в окружающем мире основаны на многократном повторении одной и той же последовательности действий. Смена времен года:. Жизнь растений ...Циклический алгоритм
Типы алгоритмов. Линейный – алгоритм, в котором все действия выполняются строго последовательно. Линейный Разветвляющийся Циклический. Линейная алгоритмическая ...Циклический алгоритм
Полное ветвление УСЛОВИЕ.Ключевые слова: ЕСЛИ…ТО…ИНАЧЕ. Неполное ветвление.
ВОПРОС ? ДЕЙСТВИЯ 1 ДА НЕТ.
Ключевые слова: ЕСЛИ…ТО…. Вы доделываете ...
Циклический алгоритм
Сколько циклических алгоритмов можно увидеть вокруг, если внимательно посмотреть на события: чередование времен года. посещения магазинов, школы или ...Циклический алгоритм
Цели:.Повторить тему «разветвляющийся алгоритм». Познакомиться с понятием циклического алгоритма, видами циклических алгоритмов. Применить изученный ...
Разветвляющийся алгоритм
Направо пойдешь коня потеряешь, прямо пойдешь голову потеряешь, налево пойдешь и коня и голову потеряешь. Сюжет русской народной сказки. Народные ...Разветвляющийся алгоритм
Цель урока:. организация работы по усвоению новых понятий, предусмотренных учебной программой, формирования знаний в области алгоритмов. Вопросы. ...Разветвляющийся алгоритм
ЕСЛИ пошел дождь, ТО надо открыть зонт. ЕСЛИ назвался груздем, ТО полезай в кузов. ЕСЛИ ласточки летают низко, ТО будет дождь, ИНАЧЕ дождя не будет. ...Конспекты
Что такое алгоритм
ПЛАН-КОНСПЕКТ УРОКА. Предмет: Информатика. Урок № 26. Тема урока: «Что такое алгоритм». Тип урока: Урок «открытия» нового знания. Деятельностная ...Циклический алгоритм
Тема урока: Циклический алгоритм. Цель урока. - познакомить учащихся с понятием циклического алгоритма типа «цикл со счетчиком»; командами «перо ...Готовый алгоритм
Кредитный отдел. . Задание «Готовый алгоритм». есть хлеб да вода? всё не беда. начало. конец. а). нет. . да. . Ответ:. ...Циклический алгоритм
Циклический алгоритм. Цель урока:. формирование понятия циклический алгоритм. Ход урока:. Орг. момент. . Проверка д.з. . . Ответить ...Виды алгоритмов. Разветвляющийся алгоритм
УРОК ИНФОРМАТИКИ ПО ТЕМЕ. «ВИДЫ АЛГОРИТМОВ. РАЗВЕТВЛЯЮЩИЙСЯ АЛГОРИТМ». Предмет:. Информатика. . Тема:. Виды алгоритмов. Разветвляющийся алгоритм. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Информатика
Содержит:44 слайд(ов)
Поделись с друзьями:
Скачать презентацию