Презентация "Реальные газы и жидкости" по физике – проект, доклад

Физика Реальные газы, жидкости и твердые тела

Реальные газы отличаются от идеальных тем, что их свойства зависят от взаимодействия молекул, т.е. от сил межмолекулярного взаимодействия – силы притяжения и силы отталкивания.

9. Реальные газы, жидкости и твердые тела

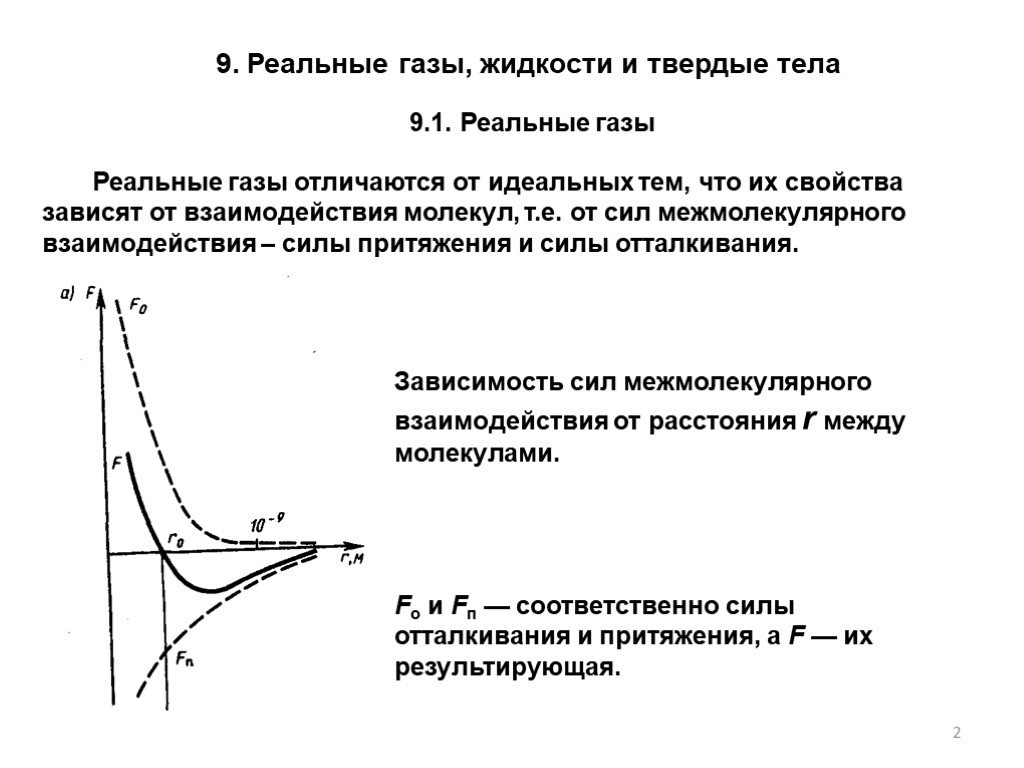
Зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами.

Fо и Fп — соответственно силы отталкивания и притяжения, a F — их результирующая.

9.1. Реальные газы

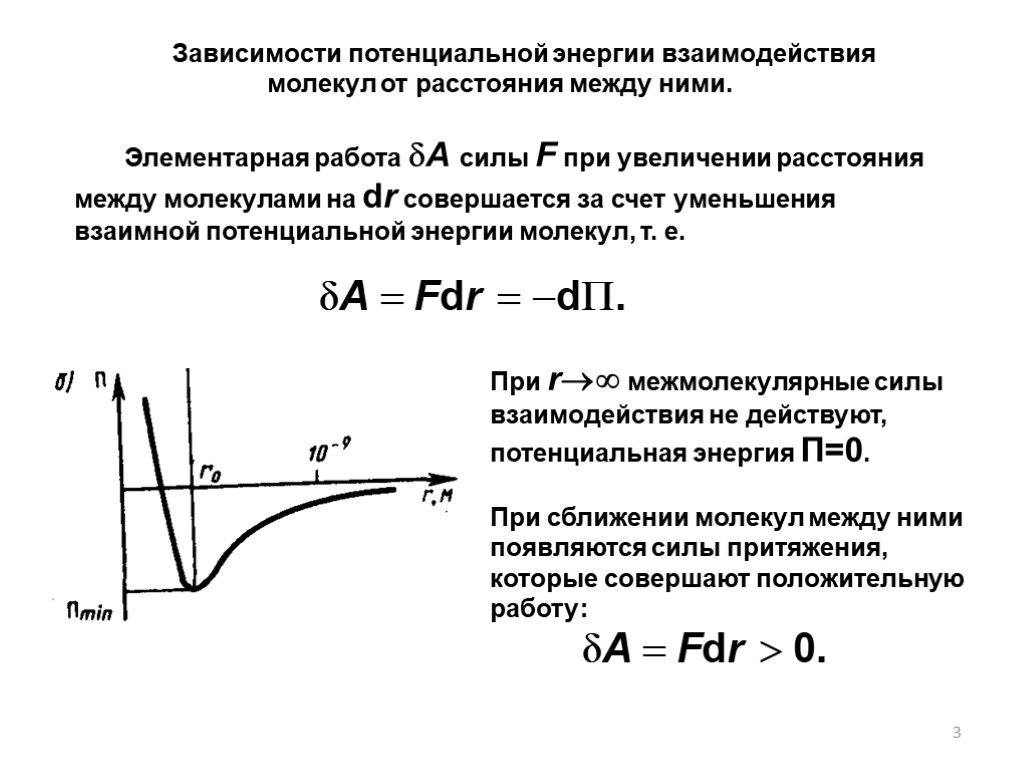
При r межмолекулярные силы взаимодействия не действуют, потенциальная энергия П=0. При сближении молекул между ними появляются силы притяжения, которые совершают положительную работу:

Зависимости потенциальной энергии взаимодействия молекул от расстояния между ними.

Элементарная работа A силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е.

Соотношение между величинами Пmin и kT является критерием различных агрегатных состояний вещества: Если Пmin>kT, то вещество находится в твердом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием r0. Если ПminkT, то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r0.

Пmin — наименьшая потенциальная энергия взаимодействия молекул — определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии

kT определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул.

9.2. Уравнение Ван-дер-Ваальса

Ван-дер-Ваальс ввел две поправки в уравнение Клапейрона — Менделеева: Учет собственного объема молекул. Фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm, а Vm – b, где b — объем, занимаемый самими молекулами. 2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением.

По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е. :

а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm — молярный объем.

С учетом поправок уравнение Ван-дер-Ваальса или уравнение состояния реальных газов для моля газа будет иметь вид:

Уравнение Ван-дер-Ваальса для произвольного количества вещества:

а и b — постоянные для каждого газа величины, определяемые опытным путем.

Изотермы Ван-дер-Ваальса

Изотермы Ван-дер-Ваальса используют для исследования поведения реального газа.

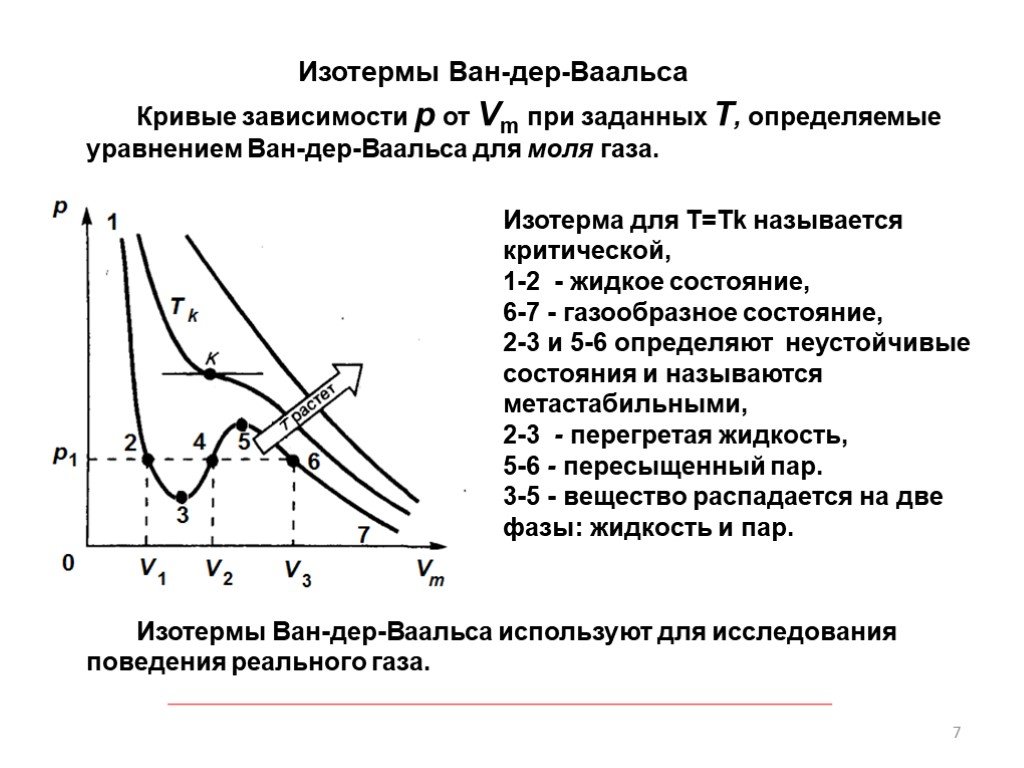
Кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа.

Изотерма для T=Tk называется критической, 1-2 - жидкое состояние, 6-7 - газообразное состояние, 2-3 и 5-6 определяют неустойчивые состояния и называются метастабильными, 2-3 - перегретая жидкость, 5-6 - пересыщенный пар. 3-5 - вещество распадается на две фазы: жидкость и пар.

9.3. Реальные жидкости. Свойства жидкостей. Поверхностное натяжение

Жидкость является агрегатным состоянием вещества, промежуточным между газообразным и твердым. В жидкостях имеет место так называемый ближний порядок в расположении частиц. Их упорядоченное расположение, повторяется на расстояниях, сравнимых с межатомными.

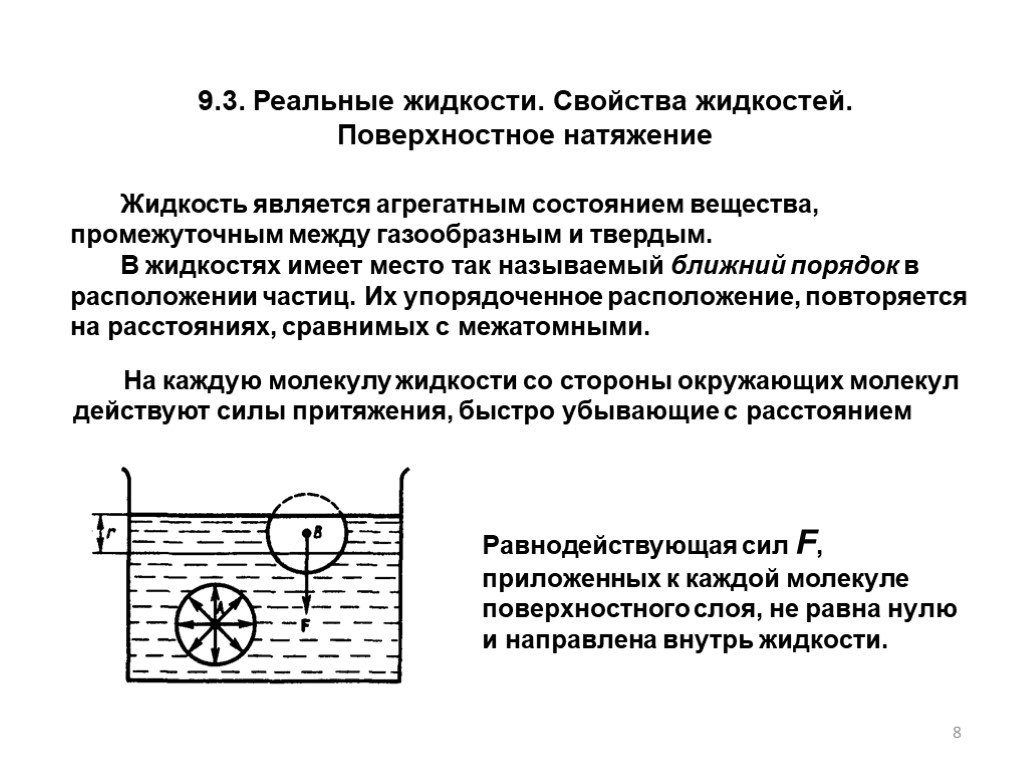
На каждую молекулу жидкости со стороны окружающих молекул действуют силы притяжения, быстро убывающие с расстоянием

Равнодействующая сил F, приложенных к каждой молекуле поверхностного слоя, не равна нулю и направлена внутрь жидкости.

Молекулы поверхностного слоя жидкости обладают большей потенциальной энергией, называемой поверхностной энергией, которая пропорциональна площади слоя S:

 — поверхностное натяжение.

Равновесное состояние характеризуется минимумом потенциальной энергии. При отсутствии внешних сил жидкость будет принимать такую форму, чтобы при заданном объеме она имела минимальную поверхность, т. е. форму шара.

Результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое молекулярным давлением.

Поверхностный слой жидкости можно представить в виде растянутой упругой пленки, в которой действуют силы натяжения.

(1)

Рассмотрим поверхность жидкости, ограниченную замкнутым контуром. Под действием сил поверхностного натяжения поверхность жидкости сократилась и рассматриваемый контур переместился в новое положение. Силы, действующие со стороны выделенного участка на граничащие с ним участки, совершают работу

f — сила поверхностного натяжения, действующая на единицу длины контура поверхности жидкости.

Из сравнения выражений (1) и (2) получим:

Работа совершается за счет уменьшения поверхностной энергии, т. е. :

(2)

Поверхностное натяжение  равно силе поверхностного натяжения, приходящейся на единицу длины контура, ограничивающего поверхность.

Единица поверхностного натяжения — (Н/м) .

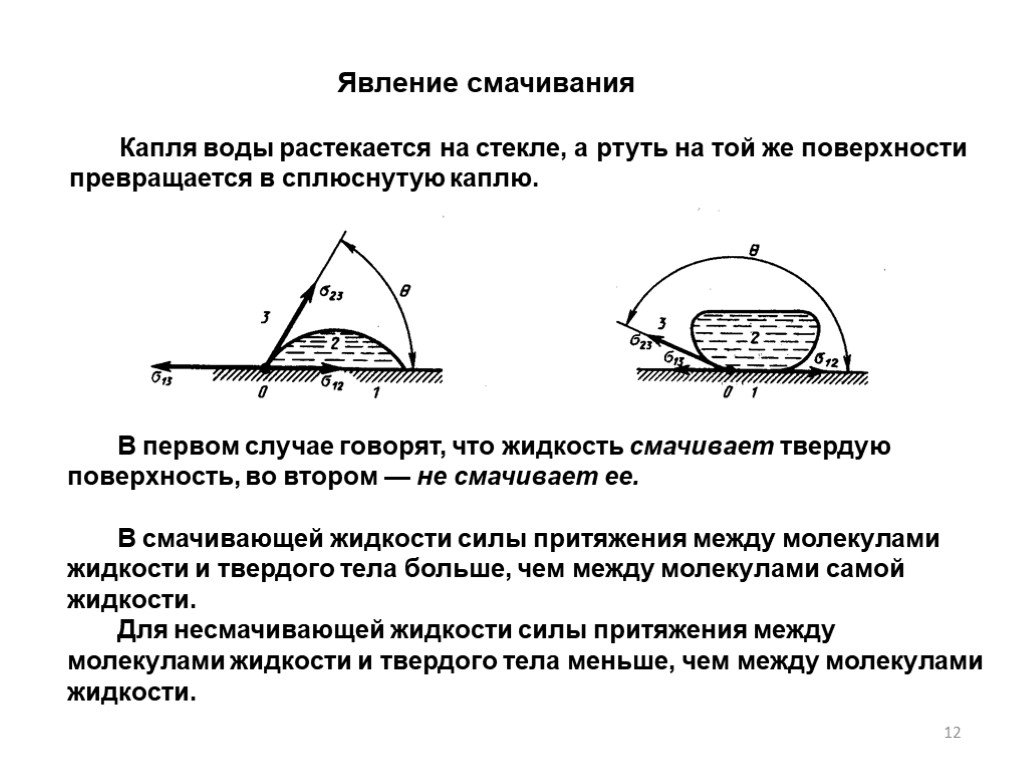
Капля воды растекается на стекле, а ртуть на той же поверхности превращается в сплюснутую каплю.

Явление смачивания

В первом случае говорят, что жидкость смачивает твердую поверхность, во втором — не смачивает ее. В смачивающей жидкости силы притяжения между молекулами жидкости и твердого тела больше, чем между молекулами самой жидкости. Для несмачивающей жидкости силы притяжения между молекулами жидкости и твердого тела меньше, чем между молекулами жидкости.

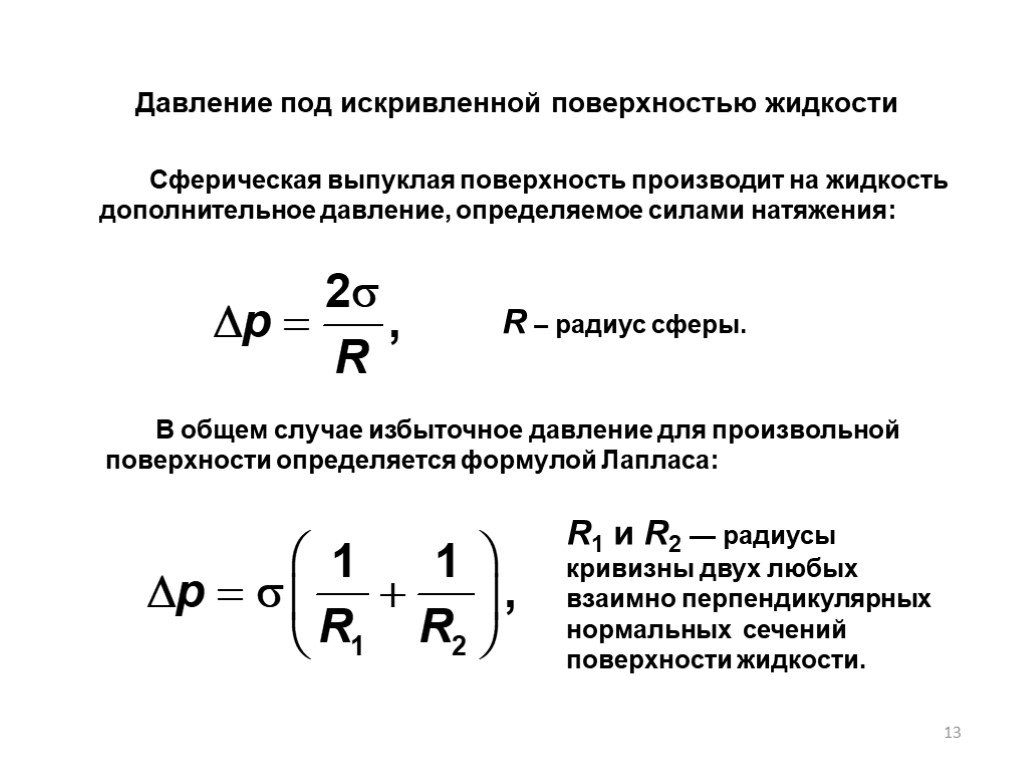
Давление под искривленной поверхностью жидкости

Сферическая выпуклая поверхность производит на жидкость дополнительное давление, определяемое силами натяжения:

R – радиус сферы.

В общем случае избыточное давление для произвольной поверхности определяется формулой Лапласа:

R1 и R2 — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости.

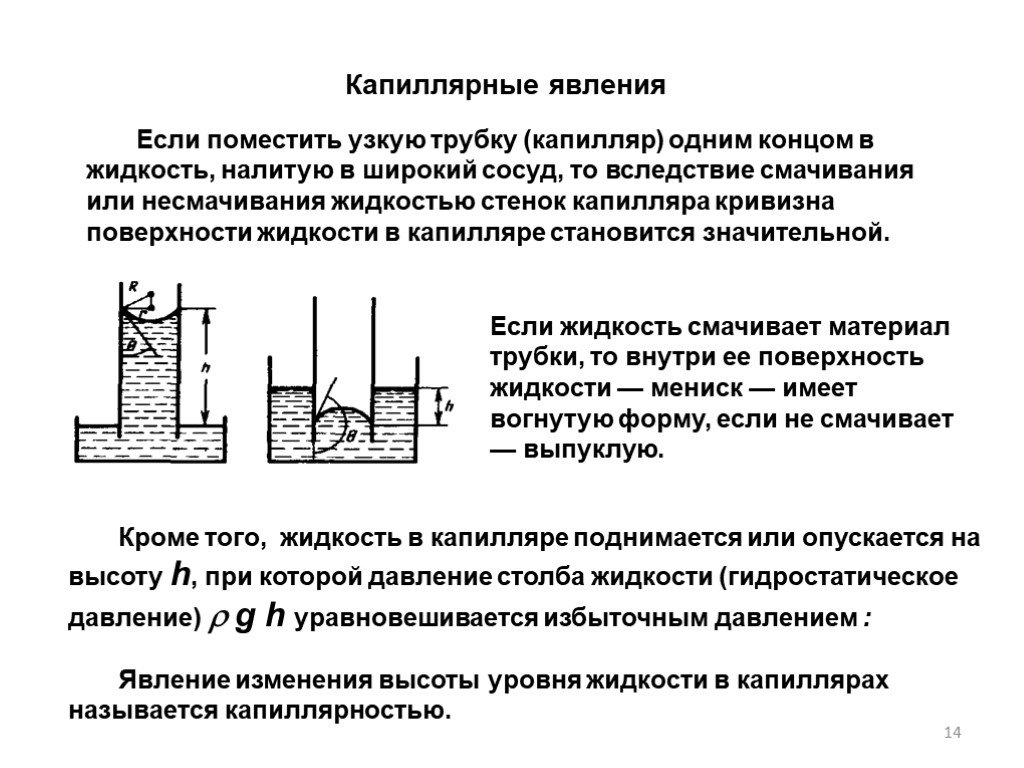
Капиллярные явления

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной.

Если жидкость смачивает материал трубки, то внутри ее поверхность жидкости — мениск — имеет вогнутую форму, если не смачивает — выпуклую.

Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью.

Кроме того, жидкость в капилляре поднимается или опускается на высоту h, при которой давление столба жидкости (гидростатическое давление)  g h уравновешивается избыточным давлением :

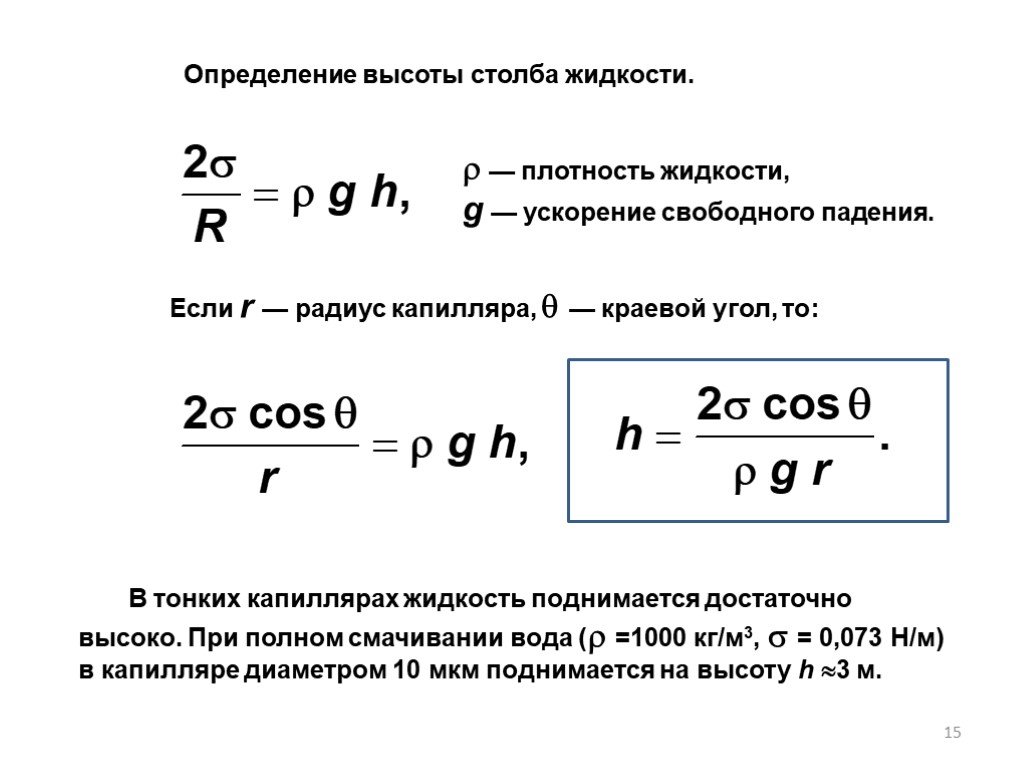
Если r — радиус капилляра,  — краевой угол, то:

В тонких капиллярах жидкость поднимается достаточно высоко. При полном смачивании вода ( =1000 кг/м3,  = 0,073 Н/м) в капилляре диаметром 10 мкм поднимается на высоту h 3 м.

 — плотность жидкости, g — ускорение свободного падения.

Определение высоты столба жидкости.

9.4. Твердые тела

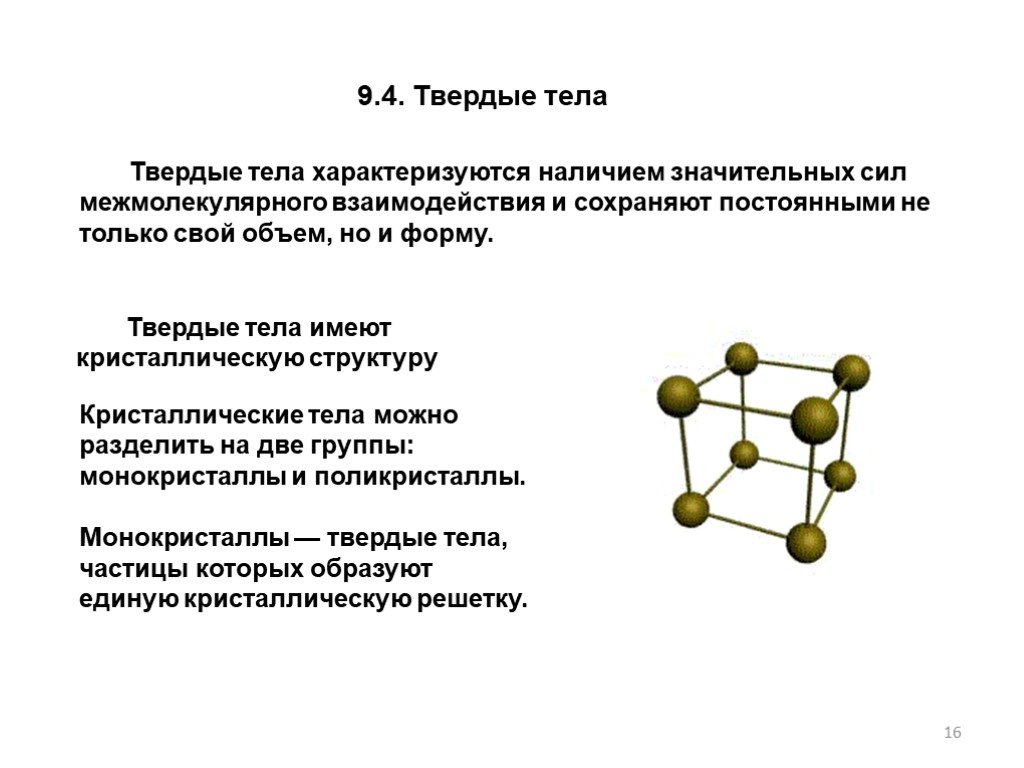
Твердые тела характеризуются наличием значительных сил межмолекулярного взаимодействия и сохраняют постоянными не только свой объем, но и форму.

Кристаллические тела можно разделить на две группы: монокристаллы и поликристаллы. Монокристаллы — твердые тела, частицы которых образуют единую кристаллическую решетку.

Твердые тела имеют кристаллическую структуру

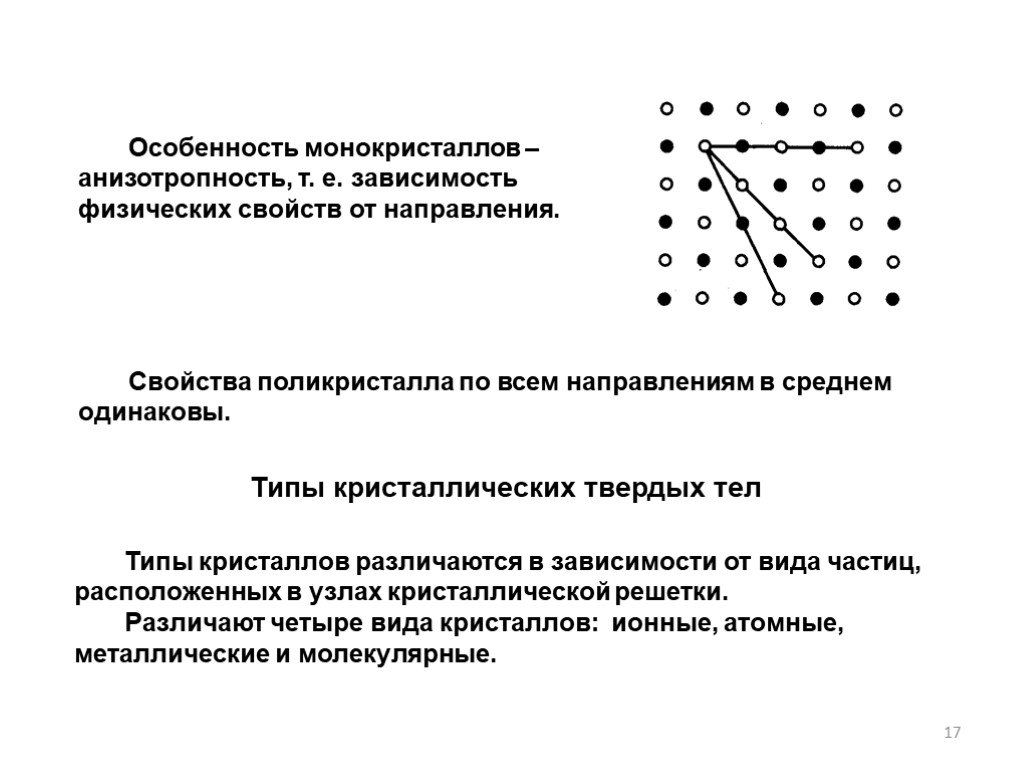
Особенность монокристаллов – анизотропность, т. е. зависимость физических свойств от направления.

Свойства поликристалла по всем направлениям в среднем одинаковы.

Типы кристаллических твердых тел

Типы кристаллов различаются в зависимости от вида частиц, расположенных в узлах кристаллической решетки. Различают четыре вида кристаллов: ионные, атомные, металлические и молекулярные.

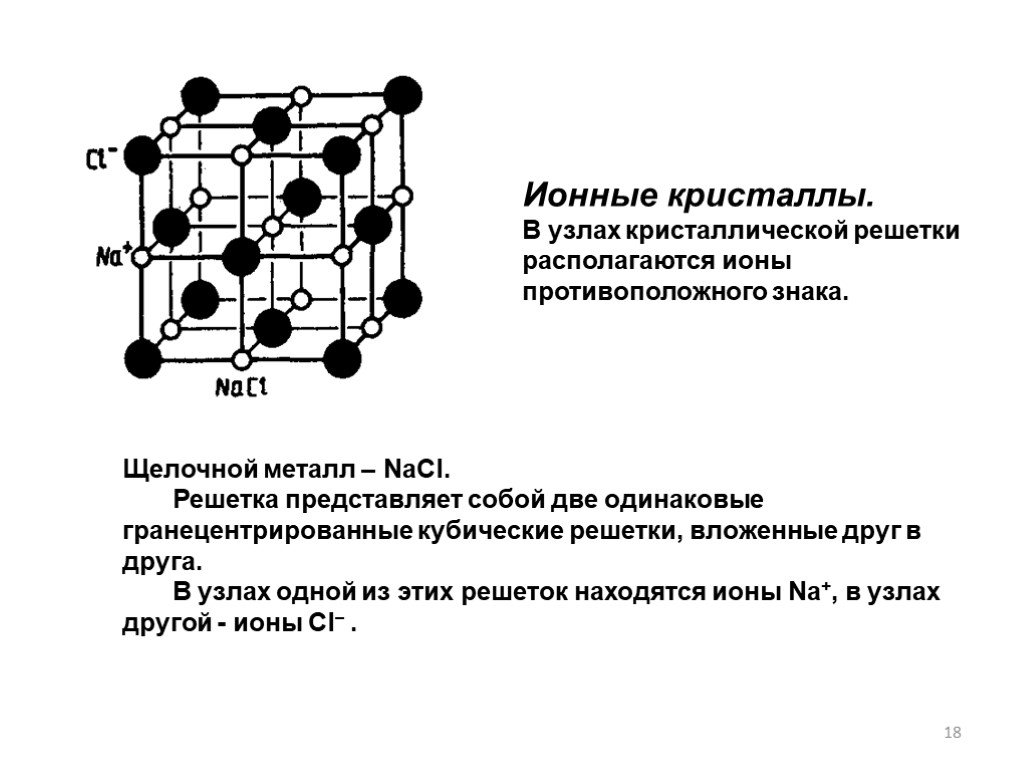
Ионные кристаллы. В узлах кристаллической решетки располагаются ионы противоположного знака.

Щелочной металл – NaCl. Решетка представляет собой две одинаковые гранецентрированные кубические решетки, вложенные друг в друга. В узлах одной из этих решеток находятся ионы Na+, в узлах другой - ионы Cl– .

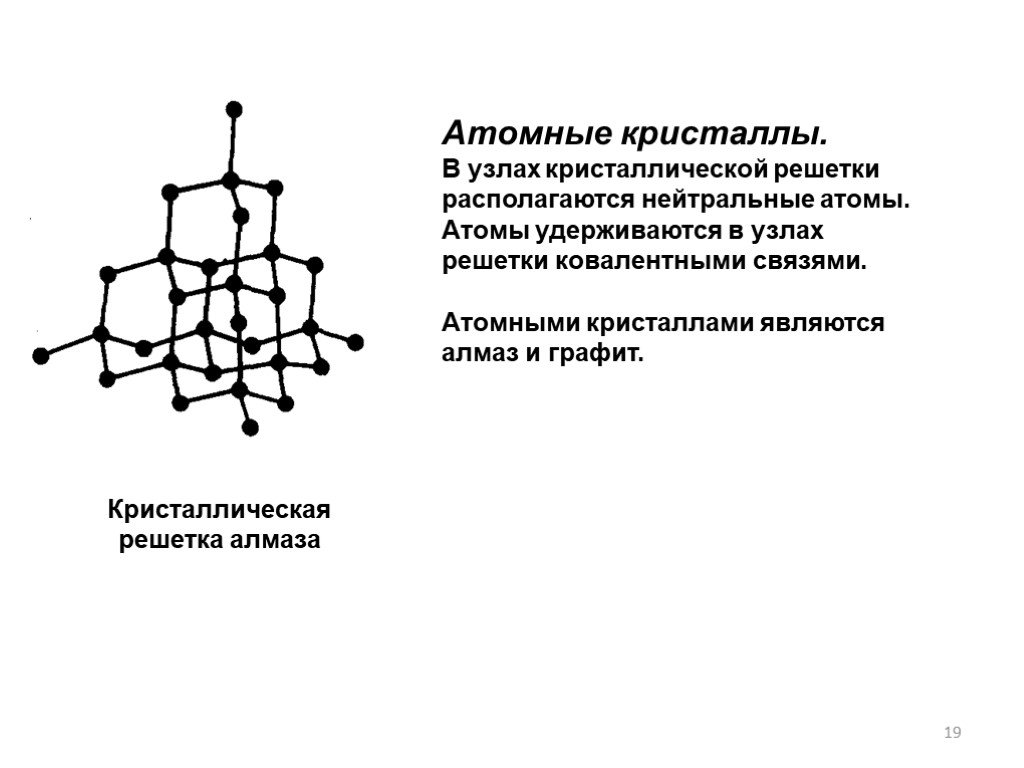
Атомные кристаллы. В узлах кристаллической решетки располагаются нейтральные атомы. Атомы удерживаются в узлах решетки ковалентными связями. Атомными кристаллами являются алмаз и графит.

Кристаллическая решетка алмаза

Металлические кристаллы. В узлах кристаллической решетки располагаются положительные ионы металла. Между положительными ионами хаотически движутся «свободные» электроны, которые обеспечивают электропроводность металлов. При образовании кристаллической решетки валентные электроны отделяются от атомов и коллективизируются: они принадлежат всему кристаллу в целом.

Молекулярные кристаллы. В узлах кристаллической решетки располагаются нейтральные молекулы вещества, силы взаимодействия между которыми обусловлены смещением электронов в электронных оболочках атомов. Молекулярными кристаллами являются большинство органических соединений, например: парафин, спирт.

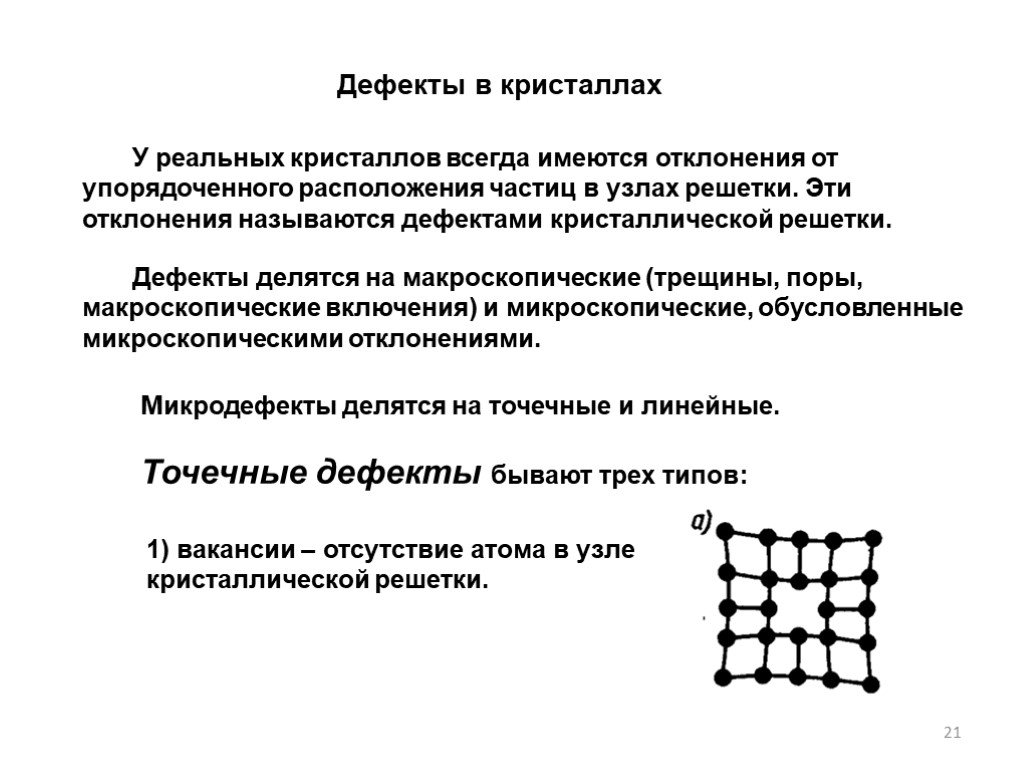
Дефекты в кристаллах

У реальных кристаллов всегда имеются отклонения от упорядоченного расположения частиц в узлах решетки. Эти отклонения называются дефектами кристаллической решетки.

Дефекты делятся на макроскопические (трещины, поры, макроскопические включения) и микроскопические, обусловленные микроскопическими отклонениями.

1) вакансии – отсутствие атома в узле кристаллической решетки.

Микродефекты делятся на точечные и линейные. Точечные дефекты бывают трех типов:

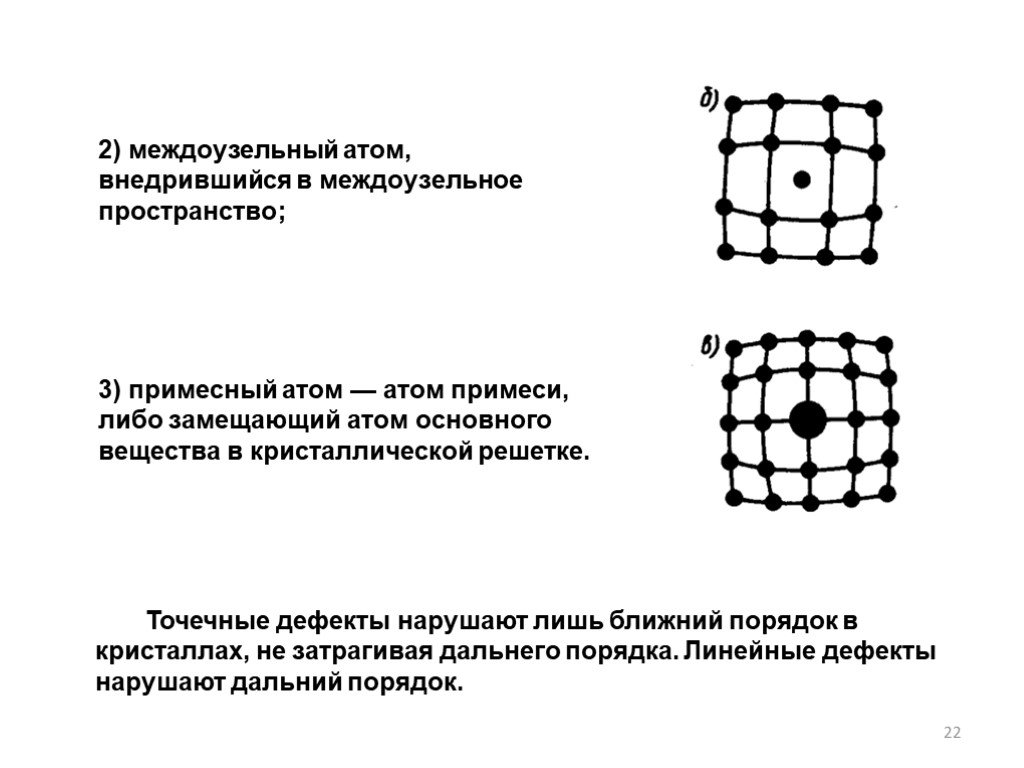
2) междоузельный атом, внедрившийся в междоузельное пространство;

3) примесный атом — атом примеси, либо замещающий атом основного вещества в кристаллической решетке.

Точечные дефекты нарушают лишь ближний порядок в кристаллах, не затрагивая дальнего порядка. Линейные дефекты нарушают дальний порядок.

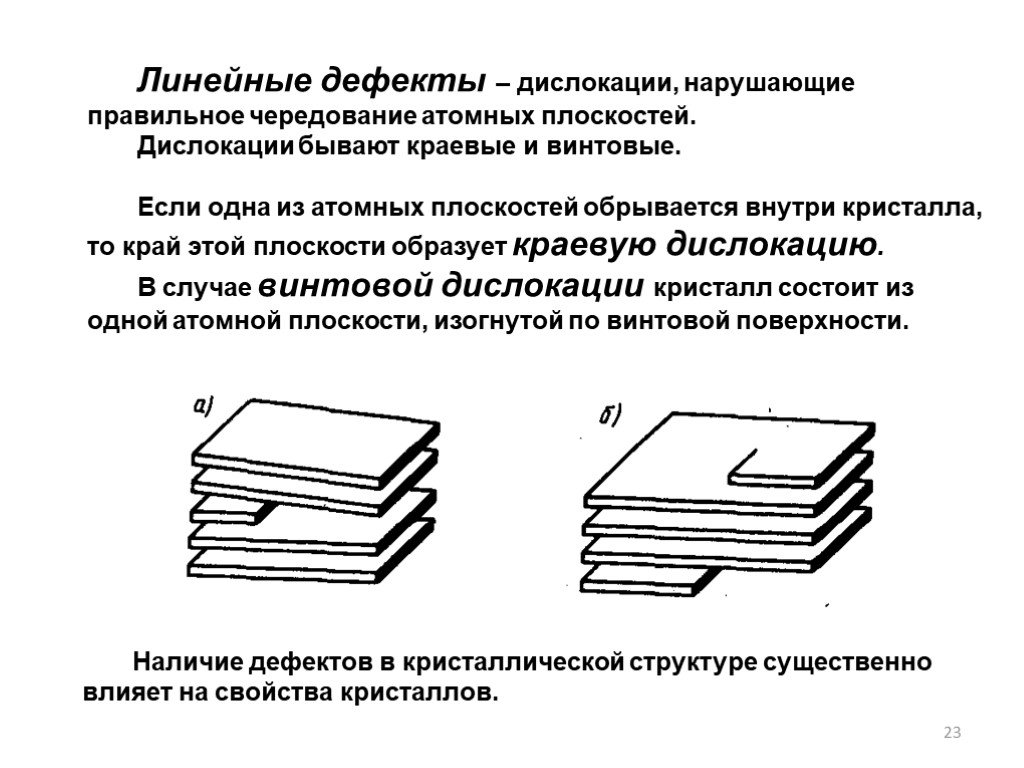
Линейные дефекты – дислокации, нарушающие правильное чередование атомных плоскостей. Дислокации бывают краевые и винтовые. Если одна из атомных плоскостей обрывается внутри кристалла, то край этой плоскости образует краевую дислокацию. В случае винтовой дислокации кристалл состоит из одной атомной плоскости, изогнутой по винтовой поверхности.

Наличие дефектов в кристаллической структуре существенно влияет на свойства кристаллов.

Теплоемкость твердых тел

В узлах кристаллической решетки частицы колеблются около своих положений равновесия в трех взаимно перпендикулярных направлениях. Каждой составляющей кристаллическую решетку частице приписывается три колебательных степени свободы, каждая из которых обладает энергией kT.

Внутренняя энергия моля твердого тела:

NA — постоянная Авогадро.

R — молярная газовая постоянная.

т. е. молярная (атомная) теплоемкость химически простых тел в кристаллическом состоянии одинакова и не зависит от температуры.

Молярная теплоемкость твердых химических соединений:

т. е. равна сумме атомных теплоемкостей элементов, составляющих это соединение.

Молярная теплоемкость твердого тела:

- закон Дюлонга и Пти.

n — число атомов в молекуле.

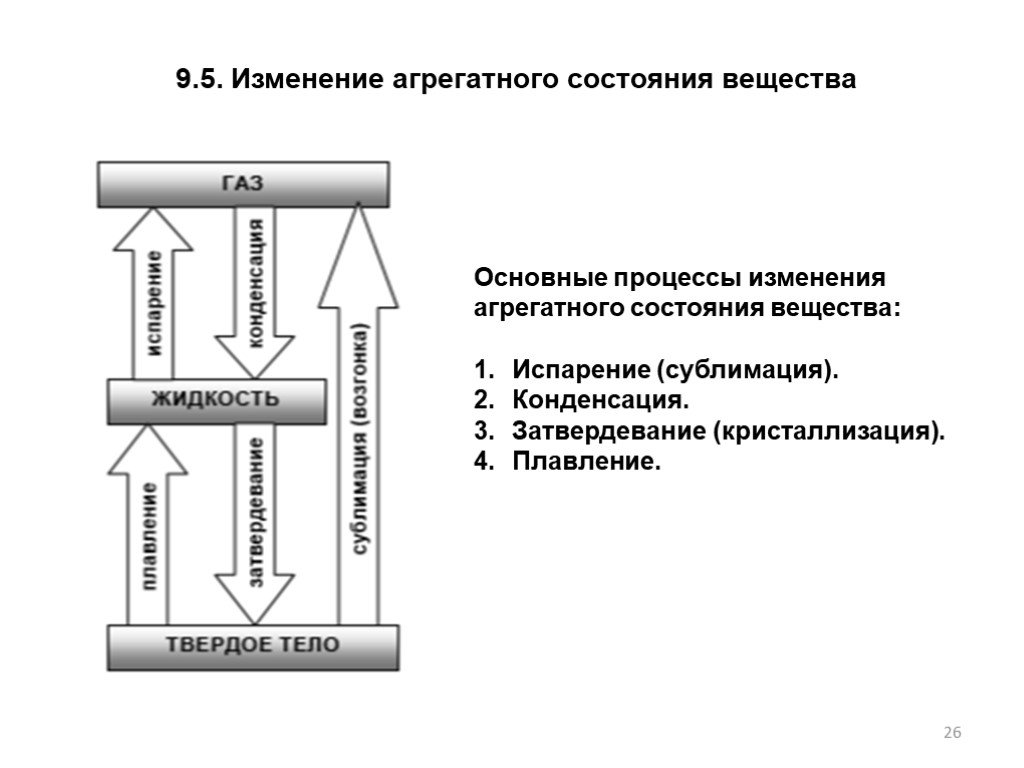
9.5. Изменение агрегатного состояния вещества

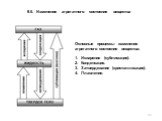
Основные процессы изменения агрегатного состояния вещества: Испарение (сублимация). Конденсация. Затвердевание (кристаллизация). Плавление.

Испарение (парообразование) – отрыв молекул от поверхности жидкости и переход в окружающее пространство. Для твердых тел это явление называется сублимация или возгонка. 2. Конденсации или превращение пара в жидкость. Процесс, компенсирующий испарение. Если число молекул, покидающих жидкость за единицу времени через единицу поверхности, равно числу молекул, переходящих из пара в жидкость, то наступает динамическое равновесие между процессами испарения и конденсации. Пар, находящийся в равновесии со своей жидкостью, называется насыщенным.

Q — количество теплоты, получаемое телом при плавлении. При температуре плавления Tпл, начинается переход тела из твердого состояния в жидкое. Температура Tпл остается постоянной до тех пор, пока весь кристалл не расплавится, и только тогда температура жидкости вновь начнет повышаться.

Зависимость Т (Q)

3. Плавление. При повышении температуры амплитуда колебаний частиц увеличивается до тех пор, пока кристаллическая решетка не разрушится, твердое тело плавится.

Количество теплоты, необходимое для расплавления 1 кг вещества, называется удельной теплотой плавления.

Q' — количество теплоты, отдаваемое телом при кристаллизации. При постоянной температуре, равной Tпл, начинается кристаллизация. Для кристаллизации вещества необходимо наличие так называемых центров кристаллизации кристаллических зародышей. При их отсутствии вещество охлаждается до температуры, меньшей температуры кристаллизации, образуя переохлажденную жидкость.

4. Затвердевание (кристаллизация).

Зависимость Т (Q’)

Ряд веществ из-за большой вязкости в сильно переохлажденном состоянии теряют текучесть, сохраняя, как в твердые тела, свою форму. Эти тела называются аморфными твердыми телами. К ним относятся смолы, мех, сургуч, стекло. Аморфные тела, являясь переохлажденными жидкостями, изотропны, т. е. их свойства во всех направлениях одинаковы. У аморфных тел отсутствует точка плавления.

Фазовые переходы

Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества.

Фазовый переход – качественное измене­ние свойств вещества при переходе из одной фазы в другую.

Фазовые переходы I рода – это переход, сопровождающийся поглощением или выделением теплоты. Фазовые переходы I рода харак­теризуются постоянством температуры, изменениями энтропии и объема. Примеры: плавление, кристаллизация и т. п.

В переходах I рода вещество переходит из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние. Степень беспорядка увеличивается, т. е., энтропия систе­мы возрастает.

Фазовые переходы II рода не связанны с поглощением или выделением теплоты и измене­нием объема. Эти переходы характеризуют­ся постоянством объема и энтропии, но скачкообразным изменением теплоемкости.

Примеры фазовых переходов II рода: 1. Переход ферромагнитных веществ (железа, никеля) при определенных давлении в температуре в парамагнитное состояние. 2. Переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое уменьшением сопротивления до нуля.

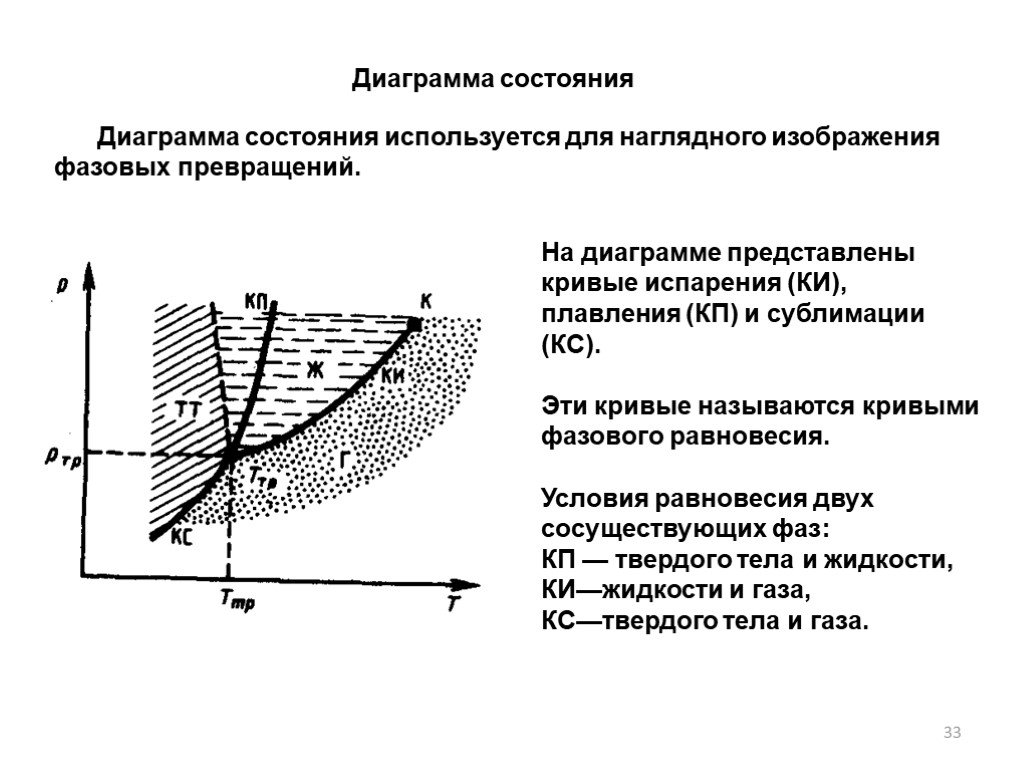
Диаграмма состо­яния используется для наглядного изображения фазовых превращений.

Диаграмма состо­яния

На диаграмме представлены кривые испарения (КИ), плавления (КП) и сублимации (КС). Эти кривые называются кривыми фазового равновесия. Условия равновесия двух сосуществующих фаз: КП — твердого тела и жидкости, КИ—жидкости и газа, КС—твердого тела и газа.

Точка пересечения кривых называется тройной точкой. Каждое вещество имеет только одну тройную точку. Тройная точка воды соответству­ет температуре 273,16 К (или температуре 0,01°С по шкале Цельсия) и является основной реперной точкой для построения термодинамической температурной шкалы.

Согласно уравнению Клапейрона — Клаузиуса, производная от равновесного давления по температуре равна:

L — теплота фазового перехода, (V2—V1) — изменение объема вещества при пере­ходе его из первой фазы во вторую, Т— температура перехода (процесс изотермичес­кий).

Метод расчета кривой равновесия двух фаз вещества

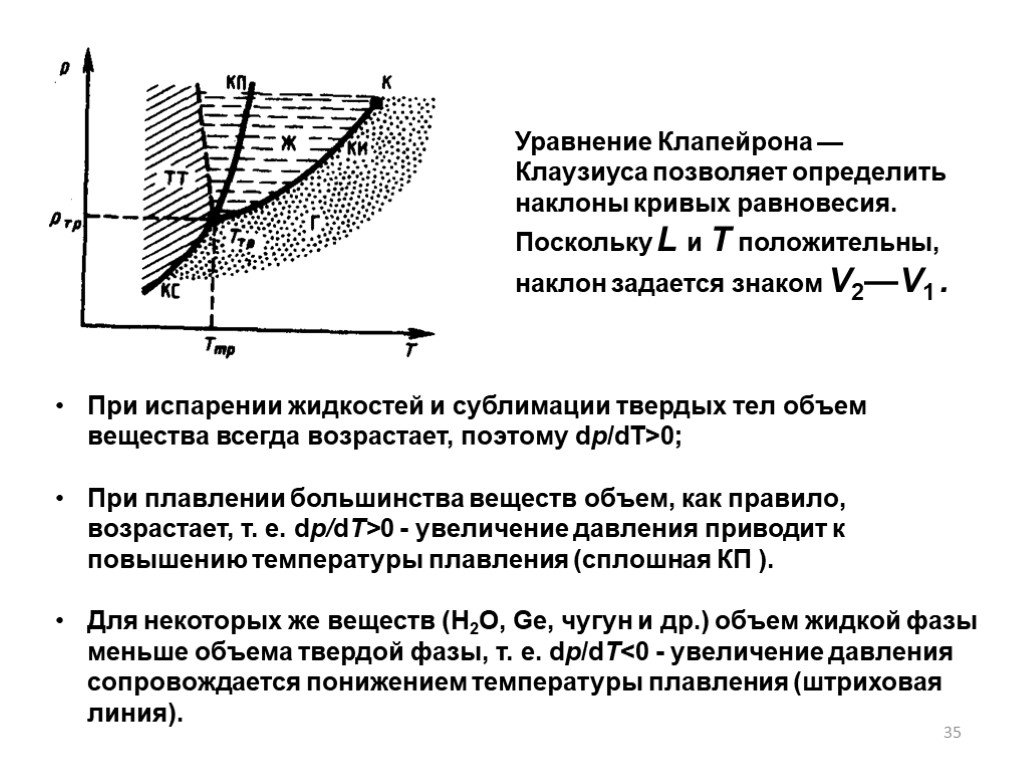
Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равно­весия. Поскольку L и Т положительны, наклон задается знаком V2—V1 .

При испарении жидкостей и сублимации твердых тел объем вещества всегда возрастает, поэтому dp/dT>0; При плавлении большинства веществ объем, как правило, возрастает, т. е. dp/dT>0 - увеличение давления приводит к повышению температуры плавления (сплошная КП ). Для некоторых же веществ (Н2О, Ge, чугун и др.) объем жидкой фазы меньше объема твердой фазы, т. е. dp/dT

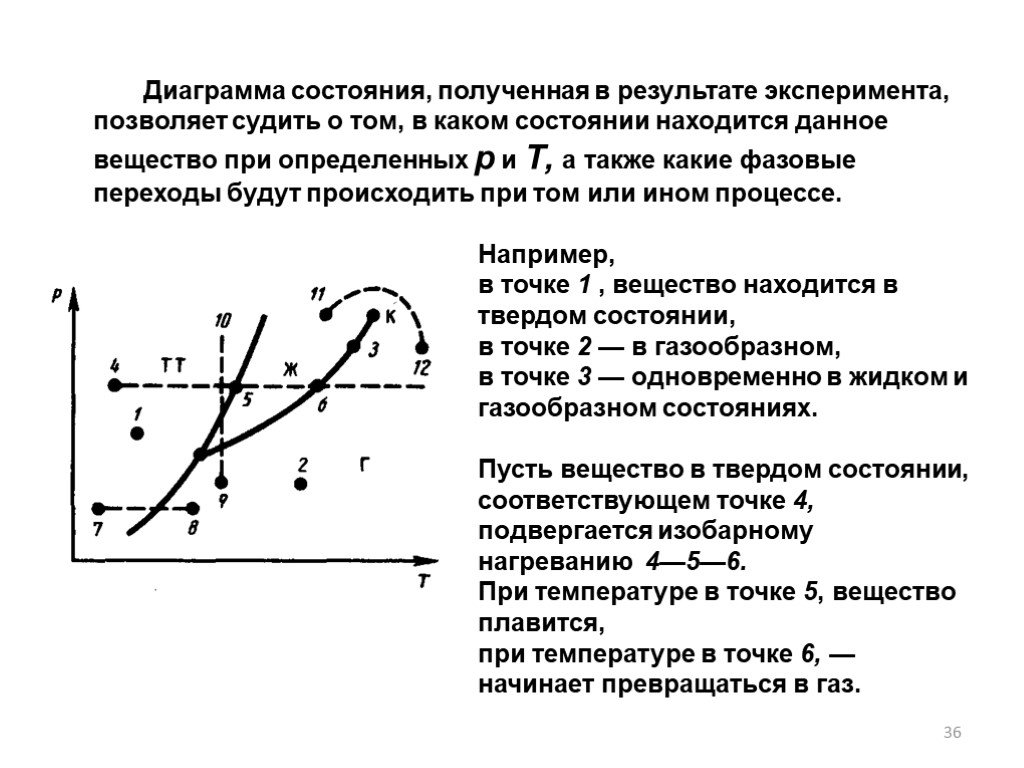
Диаграмма состояния, полученная в результате эксперимента, позволя­ет судить о том, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить при том или ином процессе.

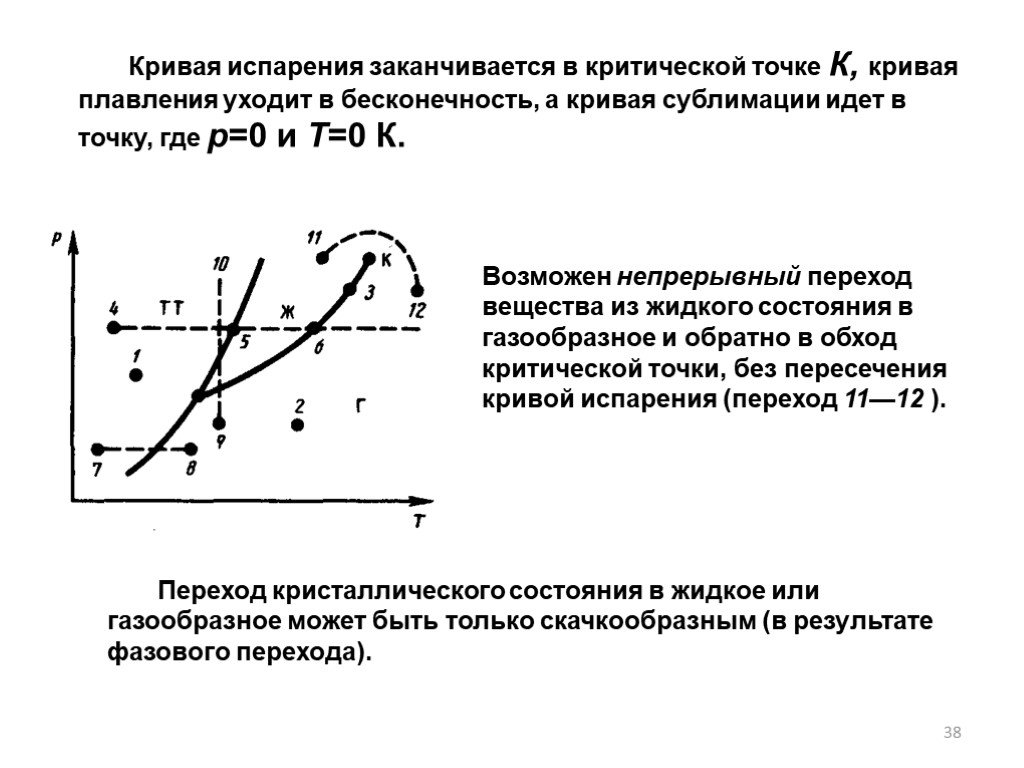
Например, в точке 1 , вещество находится в твердом состоянии, в точке 2 — в газообразном, в точке 3 — одновременно в жидком и газообразном состояниях. Пусть вещество в твердом состоянии, соответ­ствующем точке 4, подвергается изобарному нагреванию 4—5—6. При температуре в точке 5, вещество плавится, при тем­пературе в точке 6, — начинает превращаться в газ.

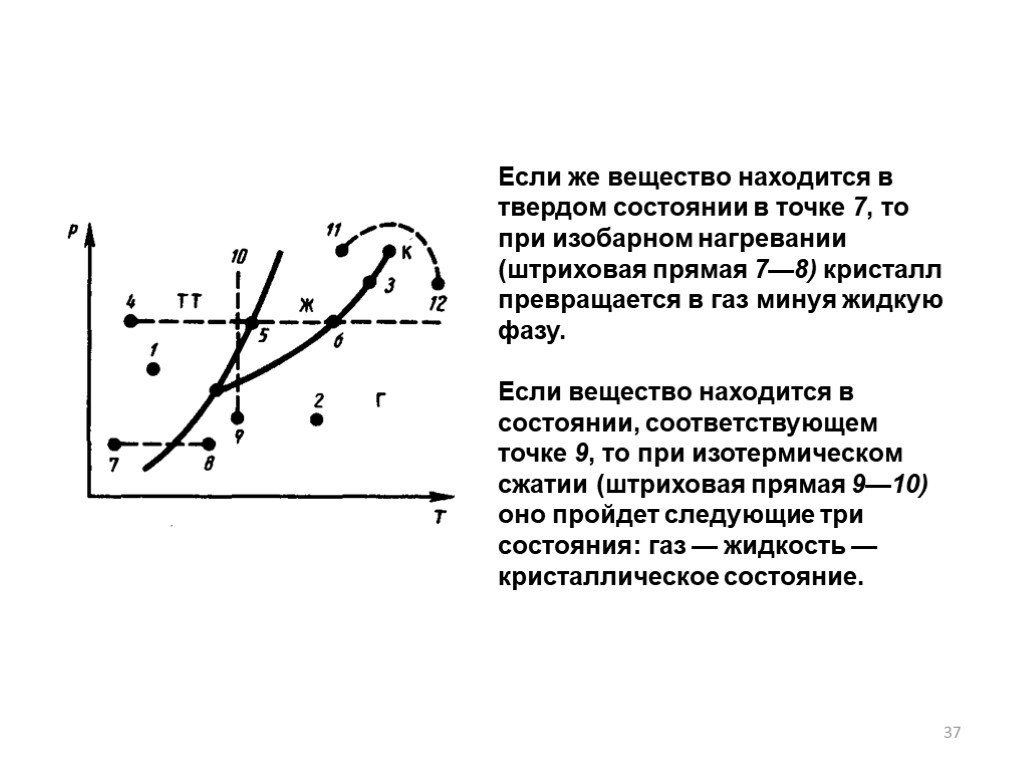
Если же вещество находится в твердом состоянии в точке 7, то при изобарном нагрева­нии (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жид­кость — кристаллическое состояние.

Возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересече­ния кривой испарения (переход 11—12 ).

Кривая испарения закан­чивается в критической точке К, кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где p=0 и T=0 К.

Переход кристаллического состояния в жидкое или газообразное может быть только скачкообраз­ным (в результате фазового перехода).