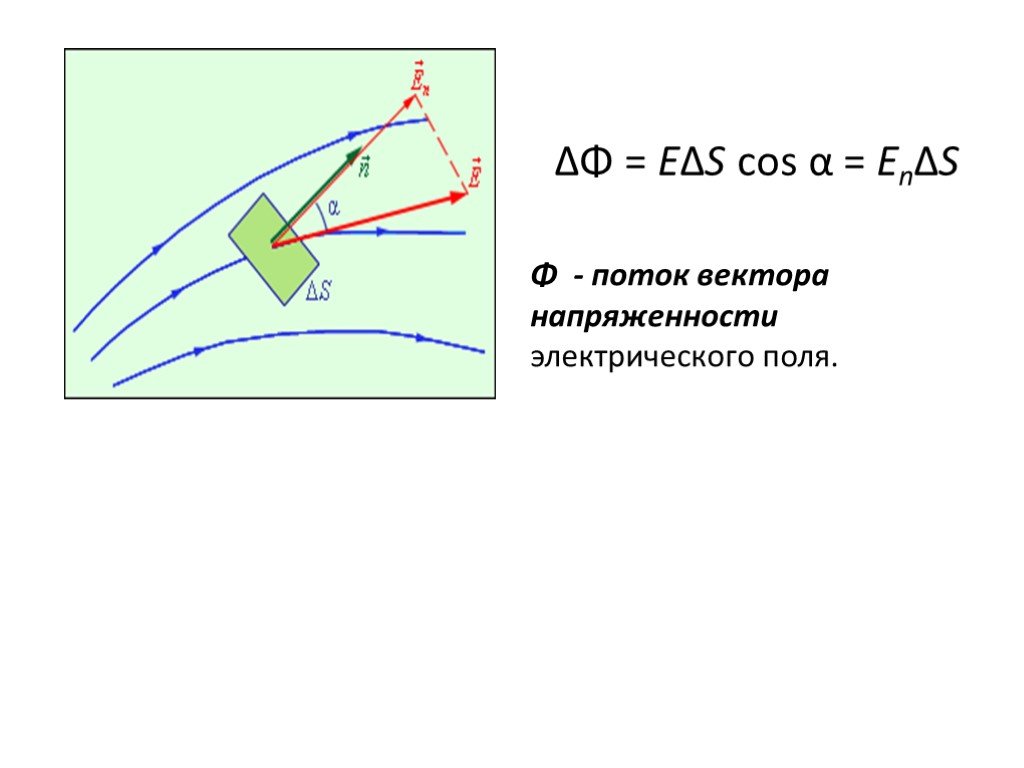
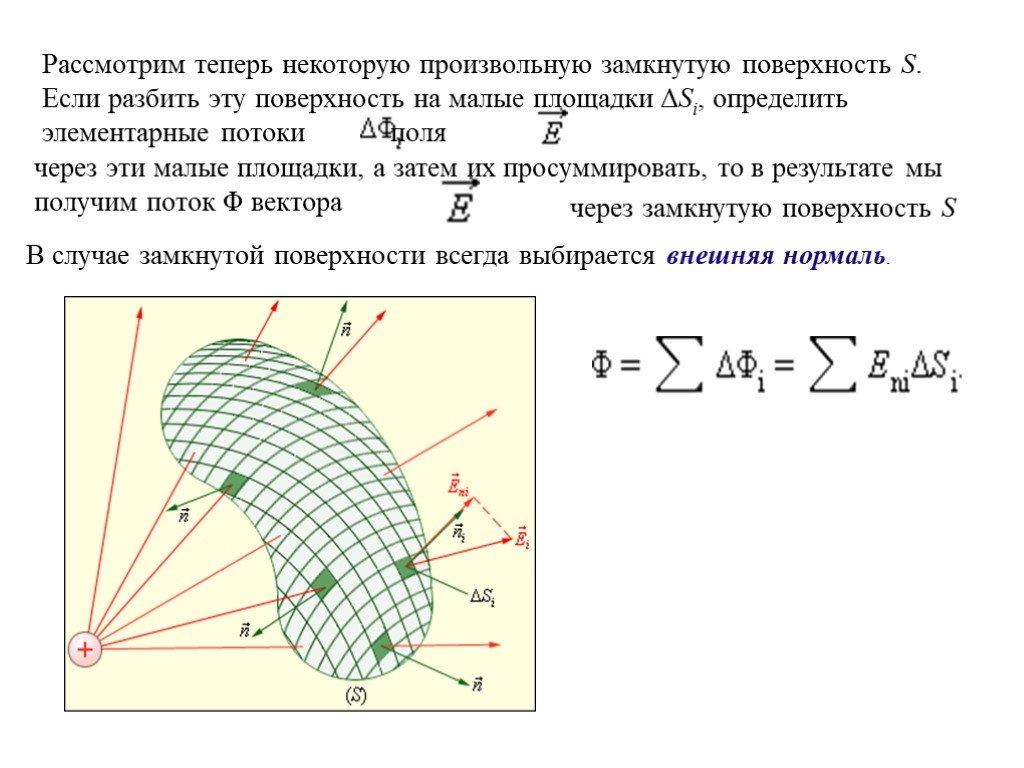
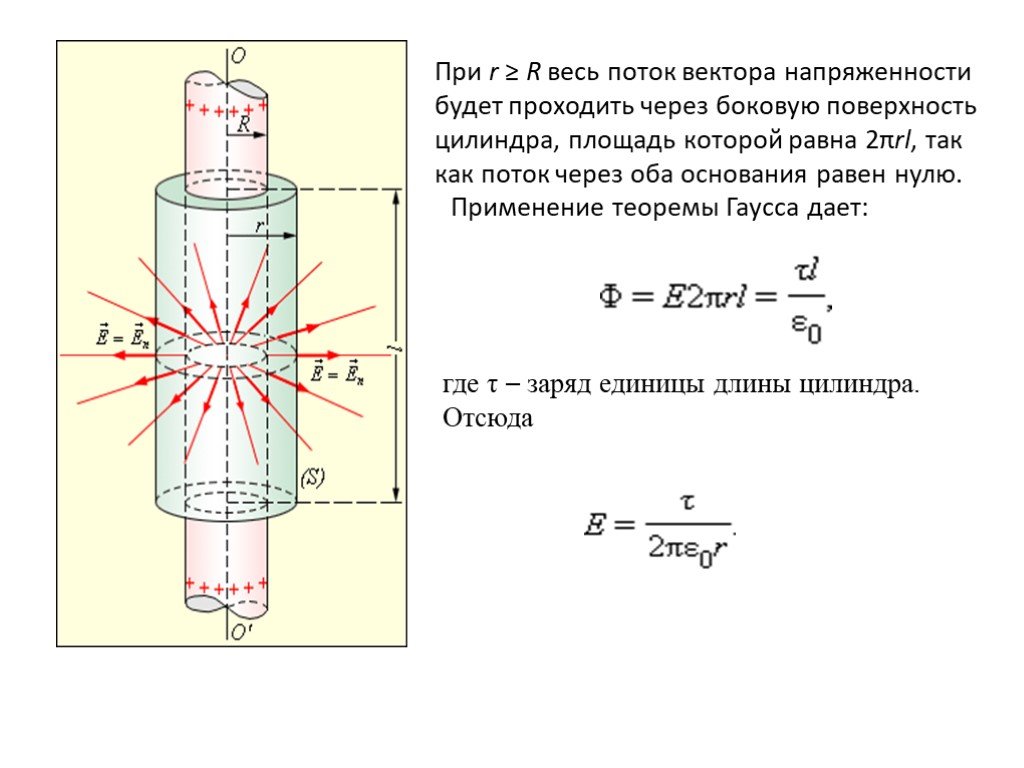
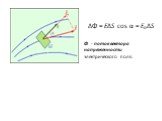
Презентация "Теорема Гаусса" по физике – проект, доклад
Презентацию на тему "Теорема Гаусса" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 7 слайд(ов).
Слайды презентации
Список похожих презентаций
Теорема об изменении кинетической энергии и уравнения Лагранжа II рода как методы изучения движения механической системы
ОБ АВТОРЕ:. Родилась я 21 мая 1989 года, в городе Ангарске. По знаку зодиака я близнецы. С самого рождения люблю животных. В нашей школе учусь с первого ...6 Момент инерции, Теорема Штейнера
Различие силы тяжести и веса. На любое тело, находящееся на поверхности Земли (кроме полюса) действует центробежная сила инерции Fцб , что и приводит ...Сила трения физика
Определение. Сила трения - это сила, возникающая в плоскости касания тел при их относительном перемещении. Направление. Сила трения направлена противоположно ...Тепловые двигатели физика
СОДЕРЖАНИЕ. Содержание Тепловой двигатель Тепловые машины и развитие техники Кто создал тепловые двигатели Виды тепловых двигателей Принцип работы ...Простая и интересная физика у Вас дома
Содержание. Эксперименты на тепловые явления. Эксперимент на плотность. Научные забавы и прочие опыты. Как будут отпадать гвозди??? Вы ответили неверно!!! ...Рентгеновские лучи физика
Презентацию подготовила: Григорьвева Наталья. Руководитель: Баева Валентина Михайловна. Цель работы: узнать о жизни и изобретении великого ученого ...Музыка и физика
Урок подготовили:. Учащиеся 9Б класса и Алевтина Антоновна Петриченко – учитель физики первой категории МОУ «СОШ № 30» г.Чебоксары. Надежда Николаевна ...Оптика и атомная физика
В основу настоящего конспекта лекций положен курс лекций по оптике, разработанный профессором кафедры оптики Н.К. Сидоровым и заведующим кафедры оптики ...Атомная физика
Факты, свидетельствующие о сложном строении атома. Периодическая система Д.И. Менделеева Электролиз Открытие электрона Катодные лучи Радиоактивность. ...Молекулярная физика и термодинамика
Литература: 1. Кудрявцев Б.Б., Курс физики: Теплота и молекулярная физика. – М.: Учпедгиз, 1960. 210 с. 2. Савельев И.В. Курс общей физики Т. 1, Механика, ...«Сообщающиеся сосуды» физика
Цель: изучить особенности сообщающихся сосудов и сформулировать основной закон сообщающихся сосудов. Опыт с двумя трубками. Опыт с сосудами разной ...«Электромагнит» физика
2. Как располагаются железные опилки в магнитном поле прямого тока? 3. Что называют магнитной линией магнитного поля? 4. Для чего вводят понятие магнитной ...«Световые волны» физика
Оглавление:. Принцип Гюйгенса Закон отражения света Закон преломления света Полное отражение Линза Расчёт увеличения линзы Дисперсия света Интерференция ...«Оптические приборы» физика
Содержание. 1.Телескоп 2.Строение телескопа 3.Разновидности телескопов 4.Рефлекторы 5.Использование телескопов 6.Микроскоп 7.Создание микроскопа 8.Использование ...«МКТ» физика
Содержание. Молекулярная физика Основы молекулярно-кинетической теории строения вещества (МКТ) Температура и внутренняя энергия тела Характеристика ...«Механические волны» физика
Цель исследования: установить с научной точки зрения, что такое звук. Задачи исследования: 1. Изучить физическую теорию звука. 2. Исследовать историю ...Атомная физика
План урока 1. Из истории физики 2. Модель Томсона 3. Опыт Резерфорда 4. Противоречия 5.Постулаты Бора 6.Энергетическая диаграмма атома водорода 7. ...Молекулярная физика
Цель: повторение основных понятий, законов и формул МОЛЕКУЛЯРНОЙ ФИЗИКИ в соответствии с кодификатором ЕГЭ. Элементы содержания, проверяемые на ЕГЭ ...Атомная физика
Атомная физика. Атомная физика на стыке XIX и ХХ вв. в науке свершились открытия, заставившие заколебаться сложившуюся картину мира. Представлениям, ...Молекулярная физика и термодинамика
Содержание:. Структура и содержание МКТ. Основные положения МКТ. Опытные обоснования МКТ. Роль диффузии и броуновского движения в природе и технике. ...Конспекты
Кинетическая энергия. Теорема об изменении кинетической энергии
Дата. Класс – 10. . Предмет: физика. Тема урока: Кинетическая энергия. Теорема об изменении кинетической энергии. Субкомпетенции:. . показать, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 ноября 2018
Категория:Физика
Содержит:7 слайд(ов)
Поделись с друзьями:
Скачать презентацию