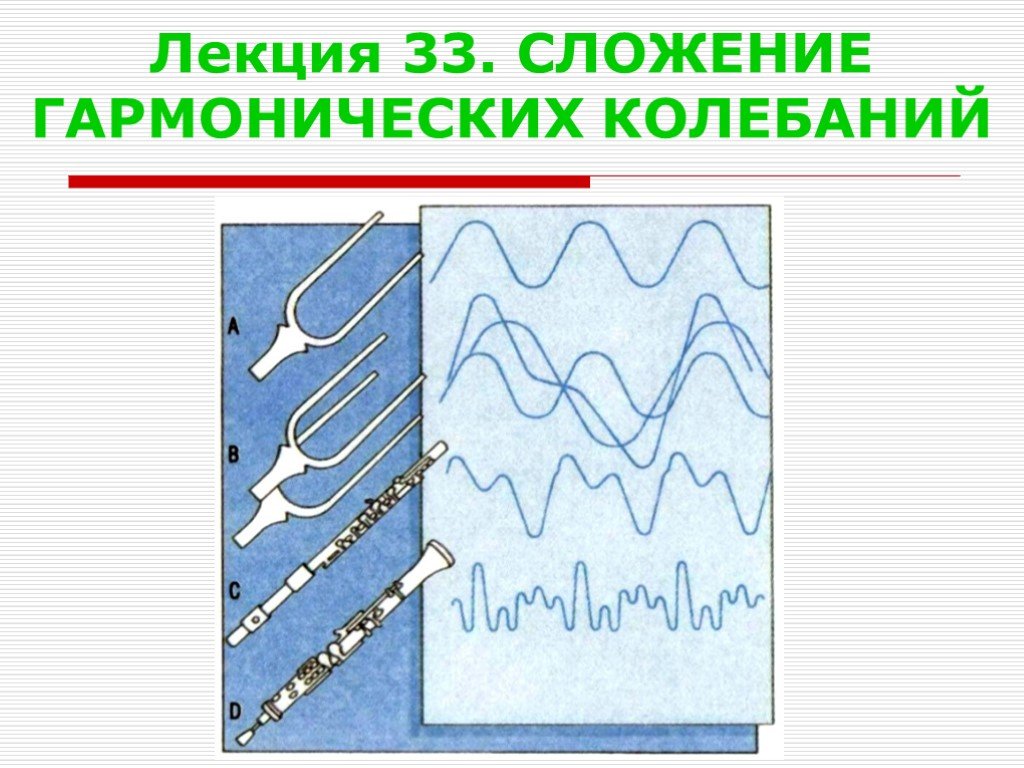
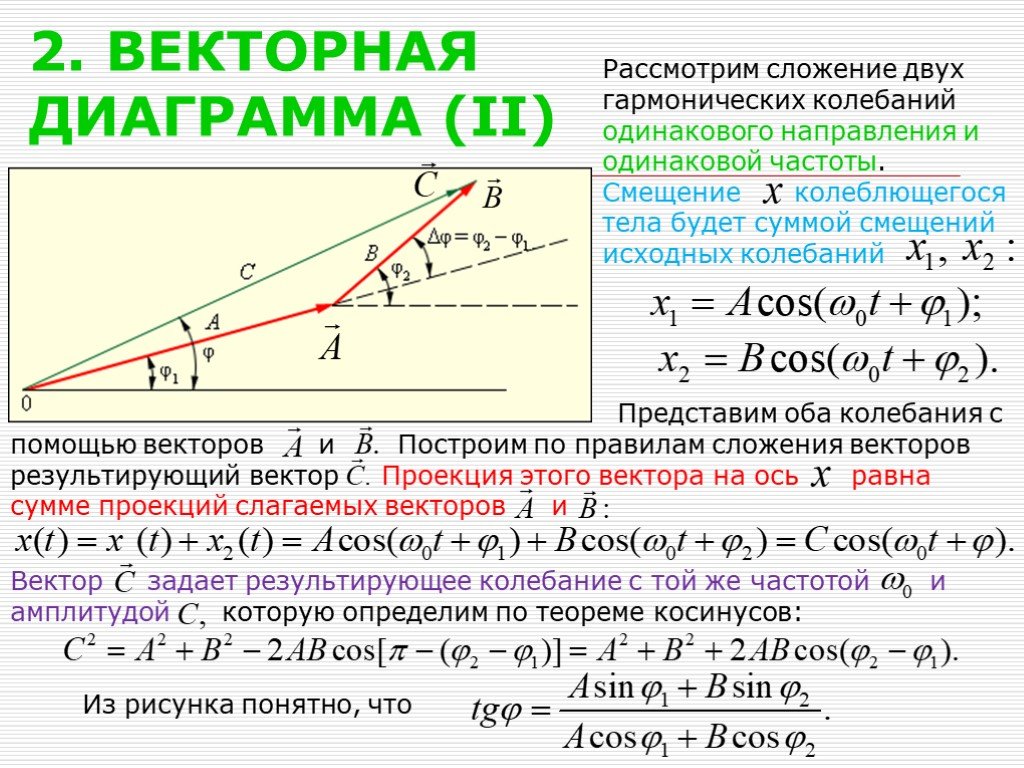
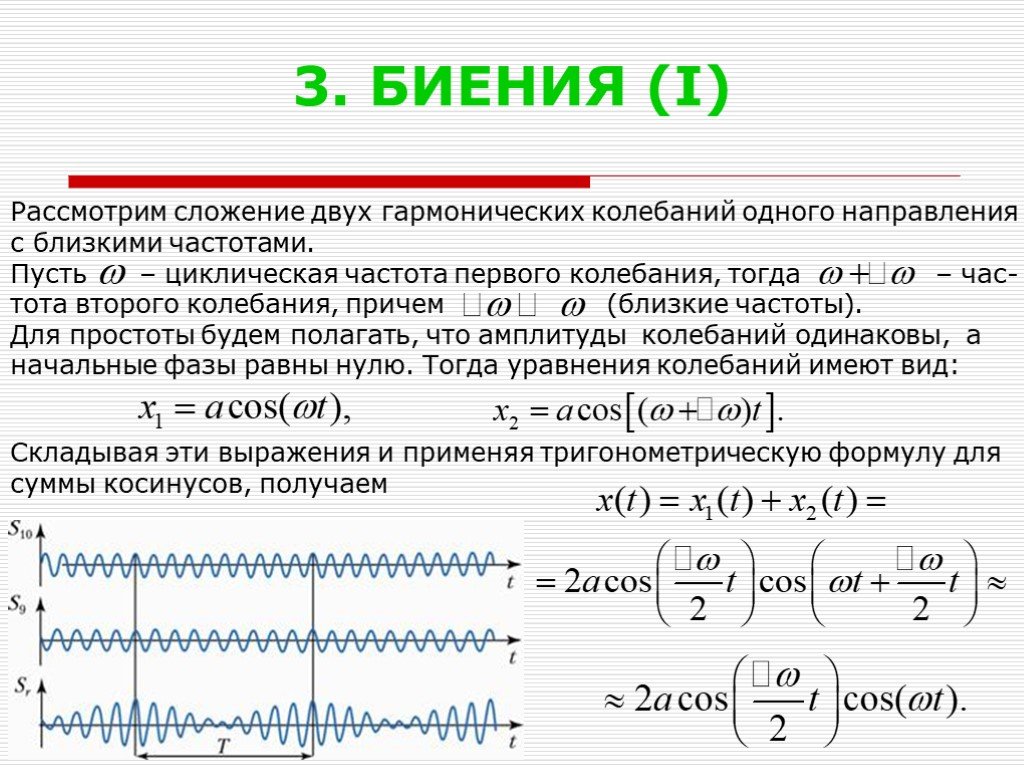
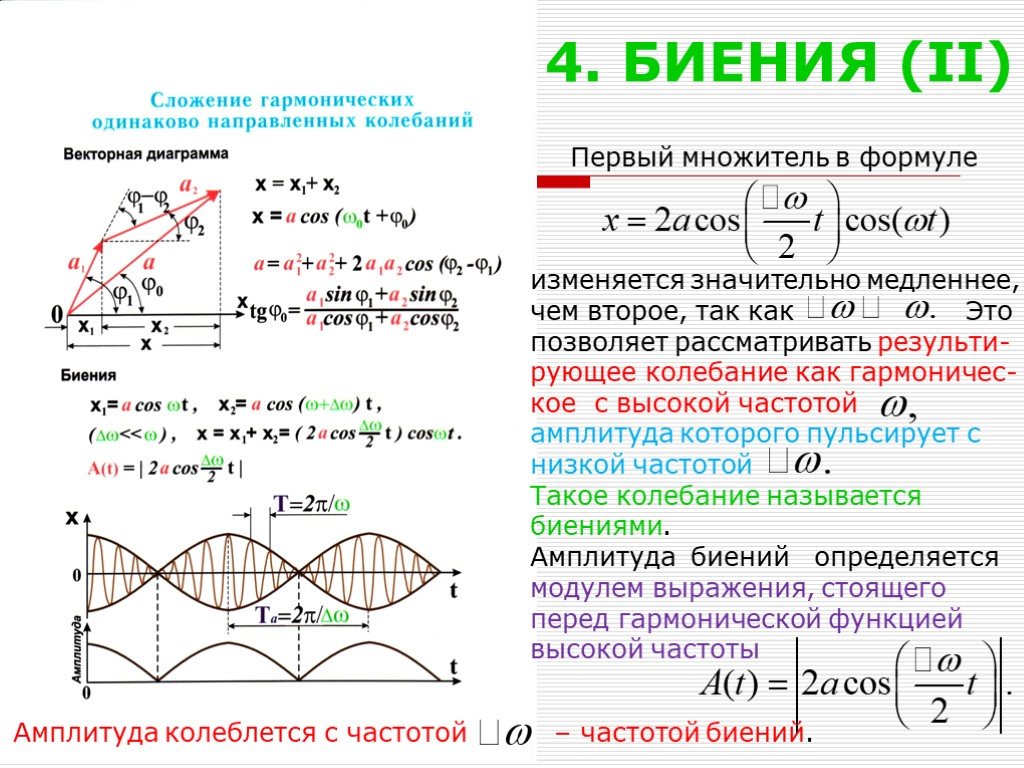
Презентация "Сложение гармонических колебаний" по физике – проект, доклад
Презентацию на тему "Сложение гармонических колебаний" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 10 слайд(ов).
Слайды презентации
Список похожих презентаций
Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил. Обозначение: ...Сложение скоростей
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ. Характеристики движения a) средняя скорость (весь путь разделить на всё время) vcp = s/t б) мгновенная скорость – скорость ...Сложение сил
ПЛАН:. Равнодействующая двух сил Сложение двух сил (правило параллелограмма) Сложение сонаправленных сил Сложение противоположно направленных сил. ...Сложение сил, действующих вдоль одной прямой. Равнодействующая.
Сделайте рисунок. Изобразите силы. Тяжести упругости Вес тела 1 вар. 2 вар. 1) задание 2) задание 3) задание. 1 вар. Масса яблока 200 г . С какой ...Сложение двух сил, направленных по одной прямой
Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил. Обозначение: ...Сложение двух сил
Цели и задачи. Расширить и систематизировать знания о силах, приложенных к телу; Ввести понятие равнодействующей силы, как векторной суммы всех сил, ...Свободные и вынужденные электромагнитные колебания. Колебательный контур. Период свободных электромагнитных колебаний
1. Электроёмкость. Конденсатор. Электроёмкость Обозначение: Единица измерения:. физическая величина, равная отношению заряда проводника к разности ...Уравнения колебаний
Примеры колебательных процессов. Круговая волна на поверхности жидкости, возбуждаемая точечным источником (гармонически колеблющимся шариком). Генерация ...Наблюдение вынужденных электрических колебаний
Приборы и материалы. 1)Магнит дугообразный; 2)Катушка с железным сердечником от разборного электромагнита; 3)Миллиамперметр ; 4)Комплект проводов; ...Визуализация звуковых колебаний
Основные задачи :. проанализировать литературу по теме; создать установку для получения стоячих волн; исследовать, есть ли зависимость вида изображения ...«Механические волны» физика
Цель исследования: установить с научной точки зрения, что такое звук. Задачи исследования: 1. Изучить физическую теорию звука. 2. Исследовать историю ...Молекулярная физика и термодинамика
Содержание:. Структура и содержание МКТ. Основные положения МКТ. Опытные обоснования МКТ. Роль диффузии и броуновского движения в природе и технике. ...Сила трения физика
Определение. Сила трения - это сила, возникающая в плоскости касания тел при их относительном перемещении. Направление. Сила трения направлена противоположно ...Тепловые двигатели физика
СОДЕРЖАНИЕ. Содержание Тепловой двигатель Тепловые машины и развитие техники Кто создал тепловые двигатели Виды тепловых двигателей Принцип работы ...Простая и интересная физика у Вас дома
Содержание. Эксперименты на тепловые явления. Эксперимент на плотность. Научные забавы и прочие опыты. Как будут отпадать гвозди??? Вы ответили неверно!!! ...Рентгеновские лучи физика
Презентацию подготовила: Григорьвева Наталья. Руководитель: Баева Валентина Михайловна. Цель работы: узнать о жизни и изобретении великого ученого ...Атомная физика
Факты, свидетельствующие о сложном строении атома. Периодическая система Д.И. Менделеева Электролиз Открытие электрона Катодные лучи Радиоактивность. ...Оптика и атомная физика
В основу настоящего конспекта лекций положен курс лекций по оптике, разработанный профессором кафедры оптики Н.К. Сидоровым и заведующим кафедры оптики ...«Сообщающиеся сосуды» физика
Цель: изучить особенности сообщающихся сосудов и сформулировать основной закон сообщающихся сосудов. Опыт с двумя трубками. Опыт с сосудами разной ...«Электромагнит» физика
2. Как располагаются железные опилки в магнитном поле прямого тока? 3. Что называют магнитной линией магнитного поля? 4. Для чего вводят понятие магнитной ...Конспекты
Распространение колебаний в упругой среде. Поперечные и продольные волны
План-конспект урока физики в 9 классе. Тема урока:. "Распространение колебаний в упругой среде. Поперечные и продольные волны". . Подготовила: ...Распространение колебаний в упругой среде. Волновое движение. Продольные и поперечные волны. Длина волны. Скорость распространения волн. Свойства механических волн
15.01.2015. Тема : « Распространение колебаний в упругой среде. Волновое движение. Продольные и поперечные волны. Длина волны. Скорость распространения ...Период колебаний математического и пружинного маятников
Урок по теме. :. «Период колебаний математического и пружинного маятников». . . Цель урока: Добиться понимания и выработать начальные навыки по ...Распространение колебаний в среде. Волны. Продольные и поперечные волны
Тема:. . Распространение колебаний в среде. Волны. Продольные. и поперечные волны. Слайд №1. Тип урока:. урок изучения нового материала. № ...Исследование зависимости периода механических колебаний
Муниципальное общеобразовательное учреждение лицей. Региональная педагогическая мастерская по проблеме. «Ноосферология и образование». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:10 октября 2018
Категория:Физика
Содержит:10 слайд(ов)
Поделись с друзьями:
Скачать презентацию