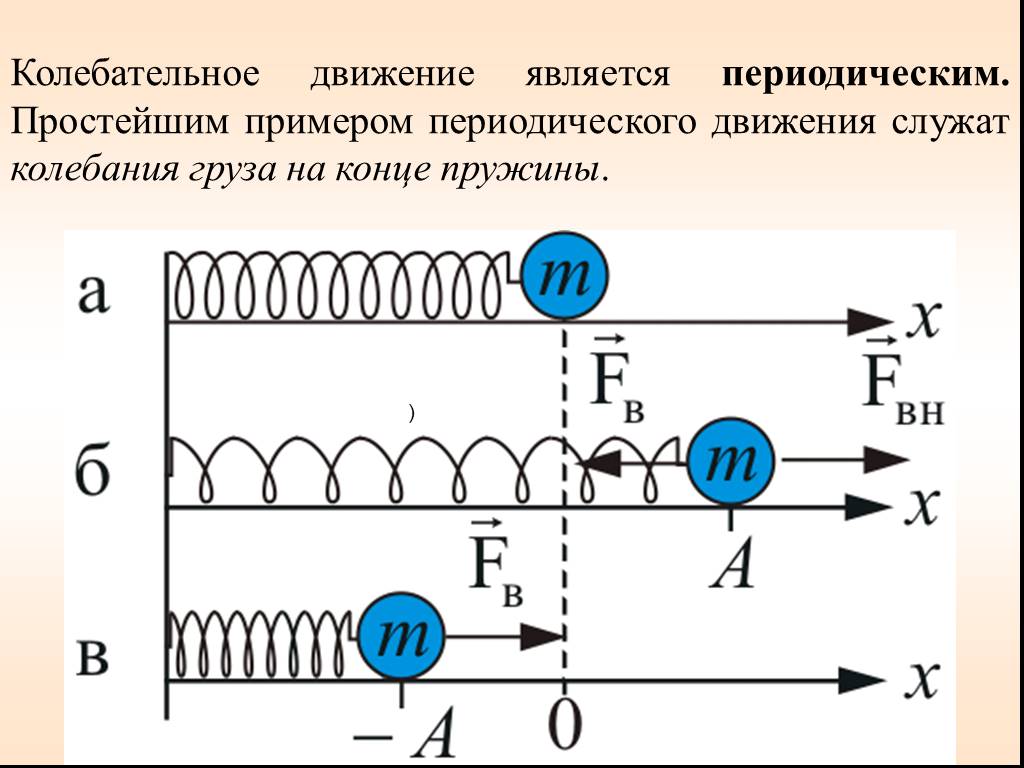
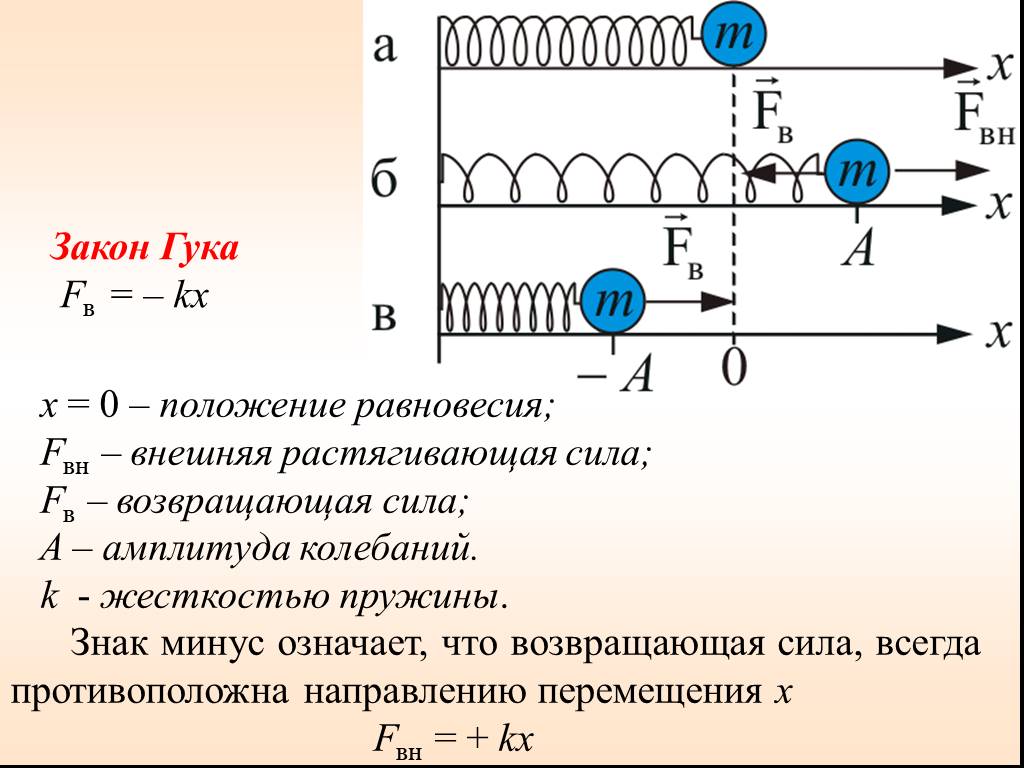
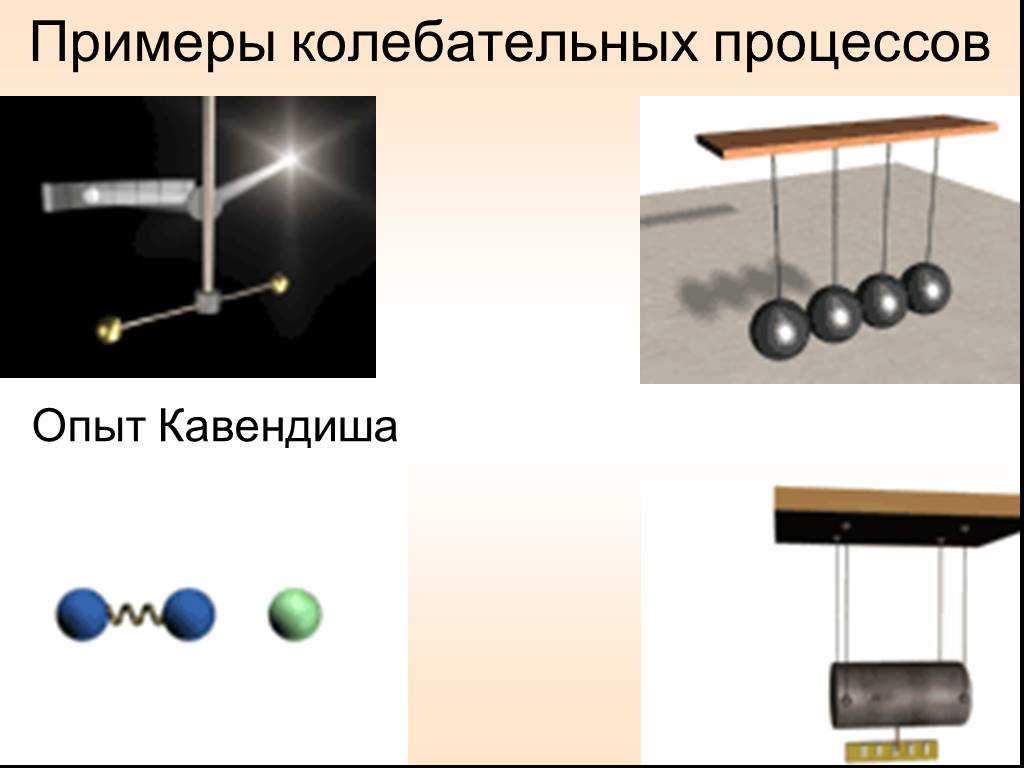
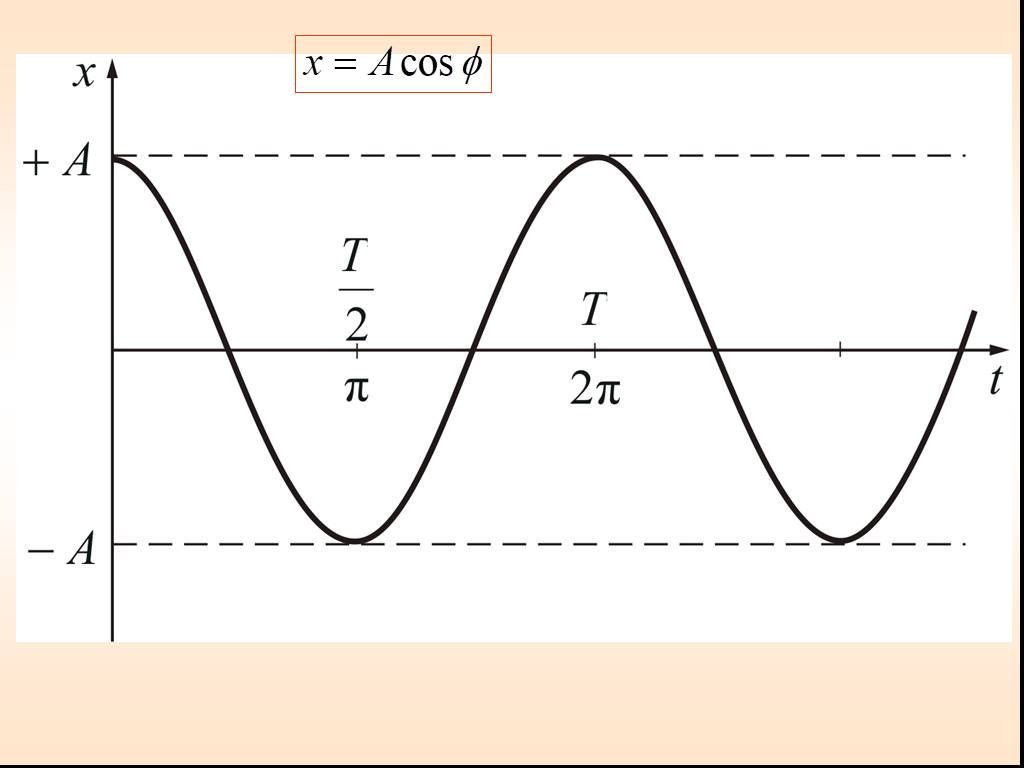
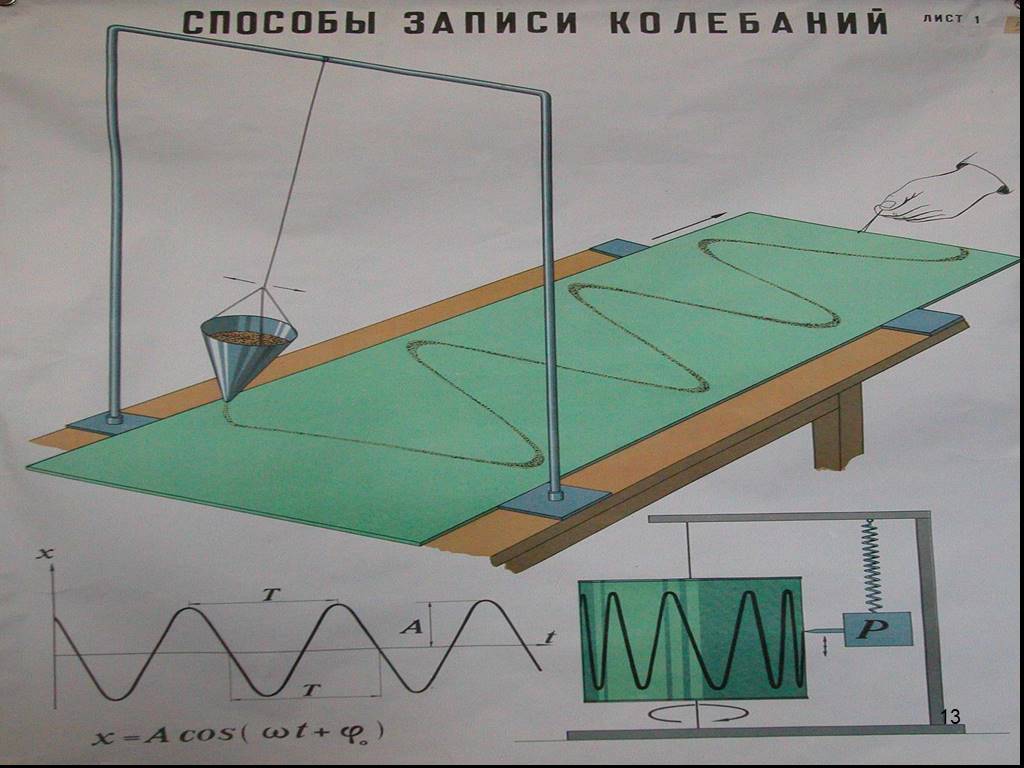
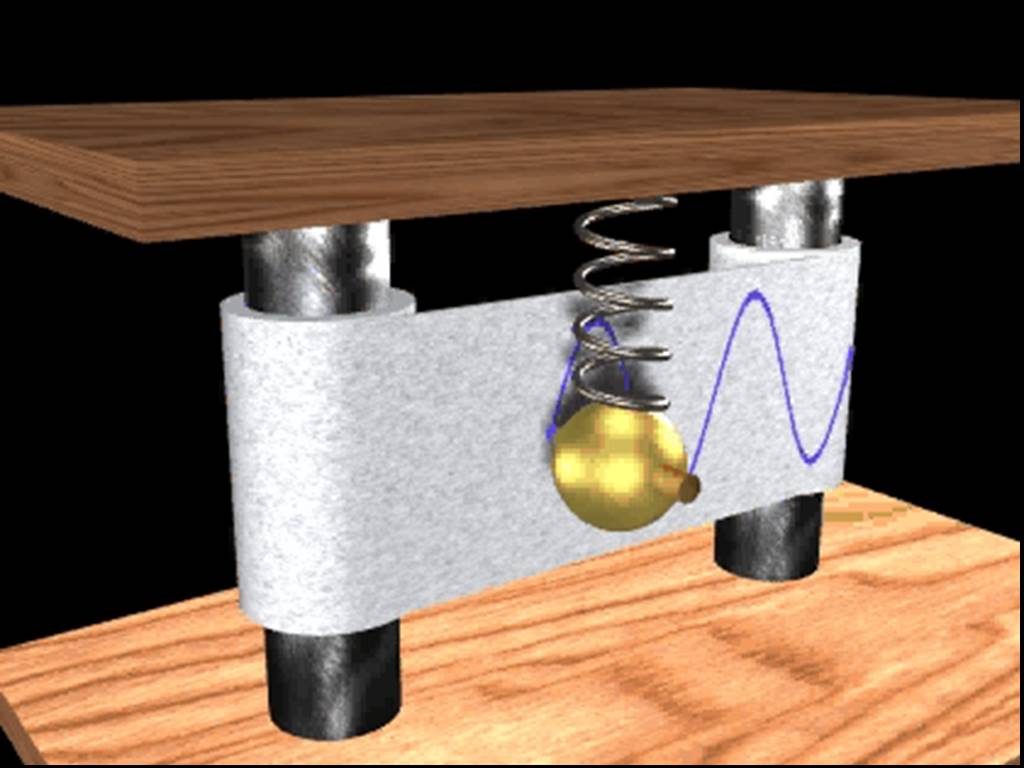
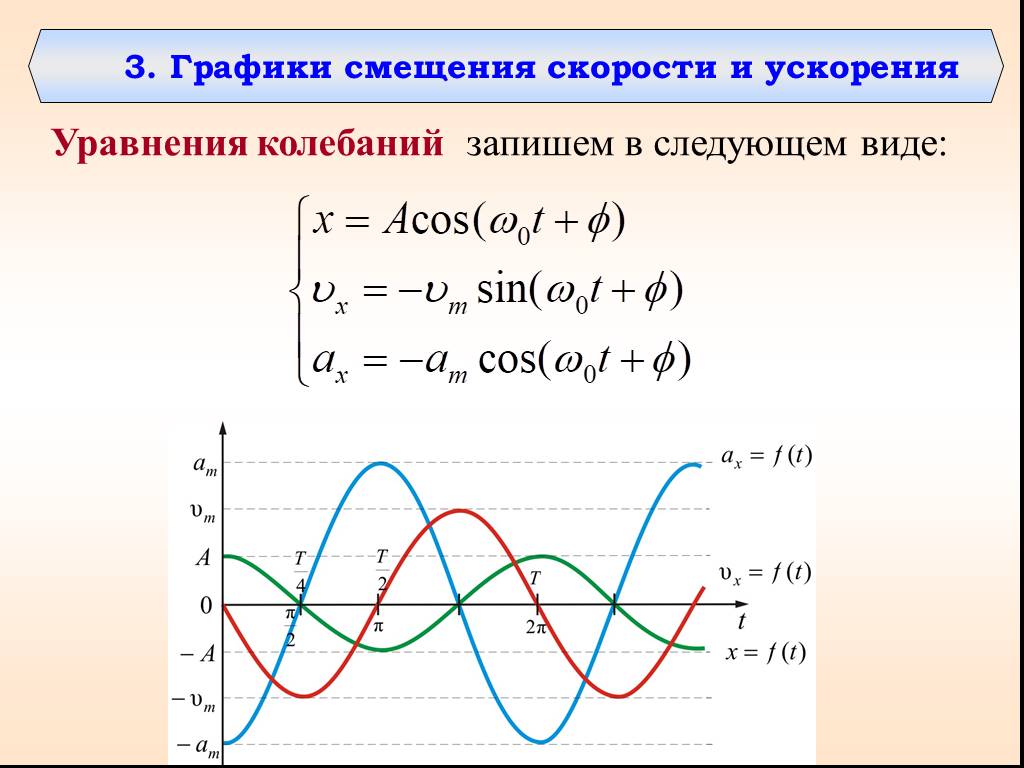
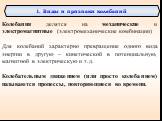
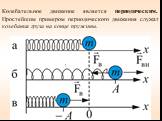
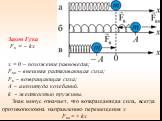
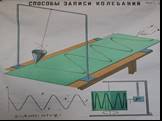
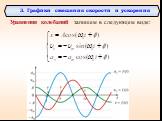
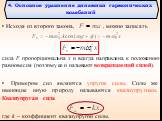
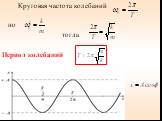
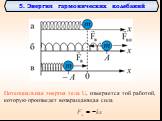
Презентация "Уравнения колебаний" по физике – проект, доклад
Презентацию на тему "Уравнения колебаний" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 67 слайд(ов).
Слайды презентации
Список похожих презентаций
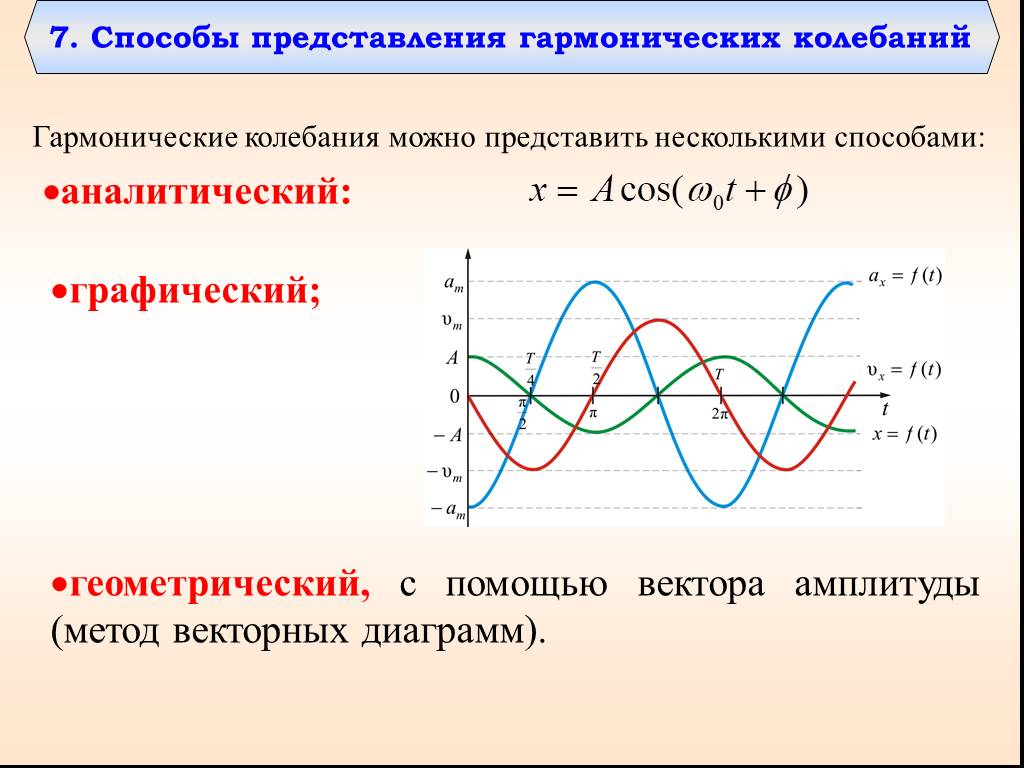
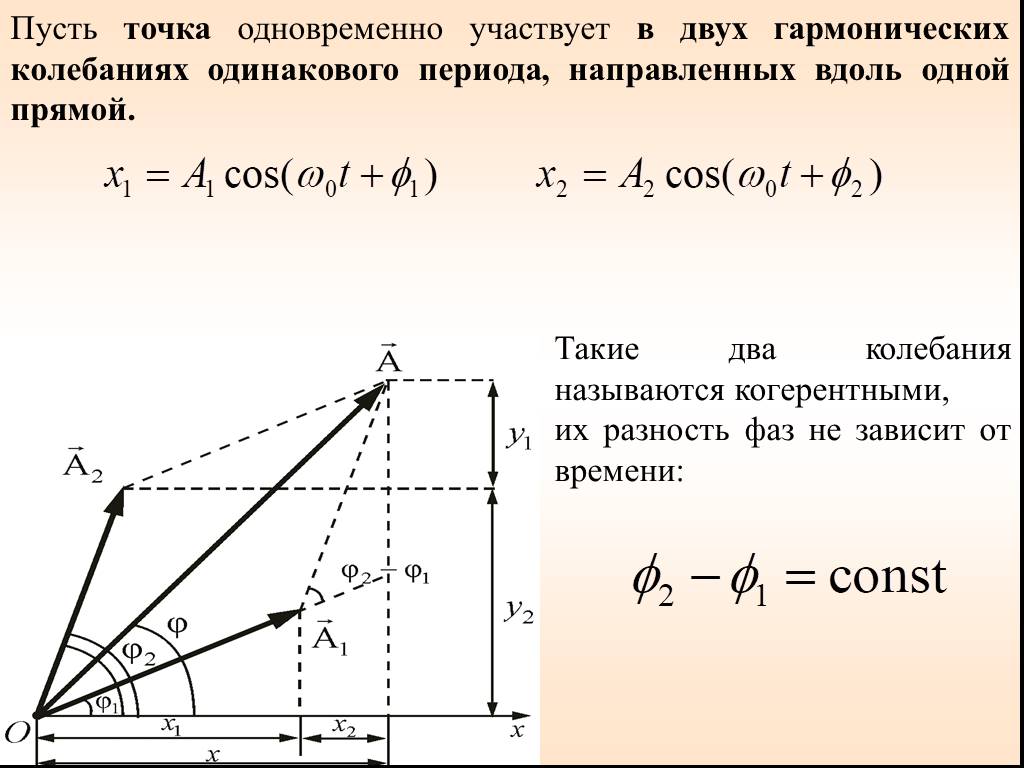
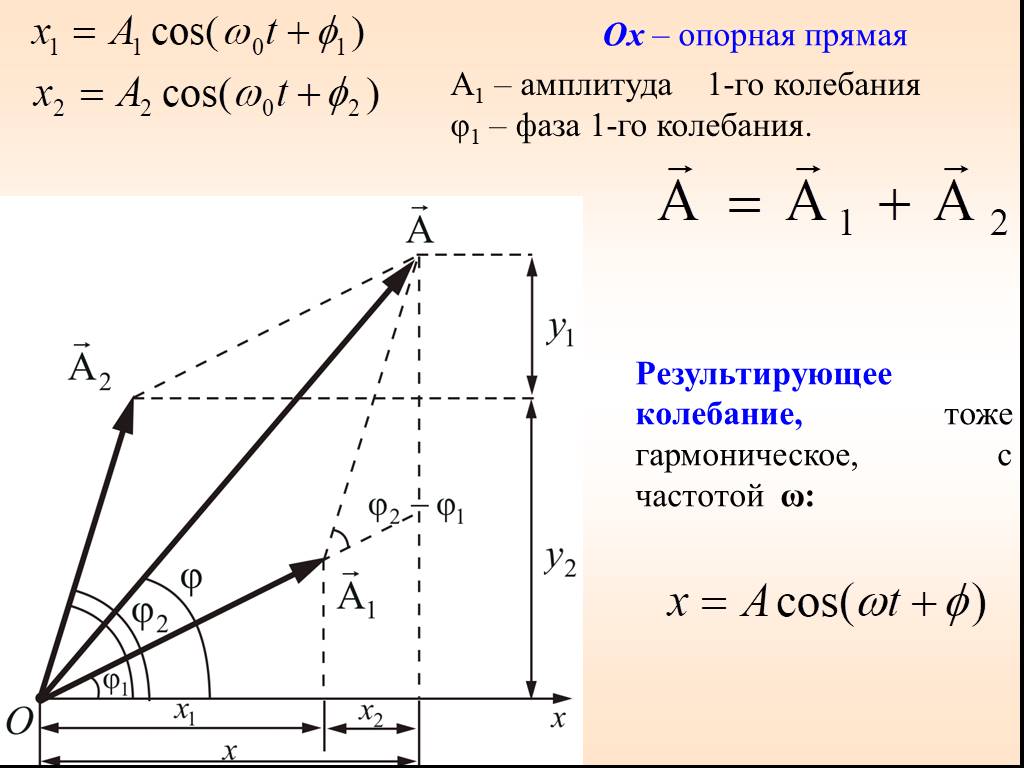
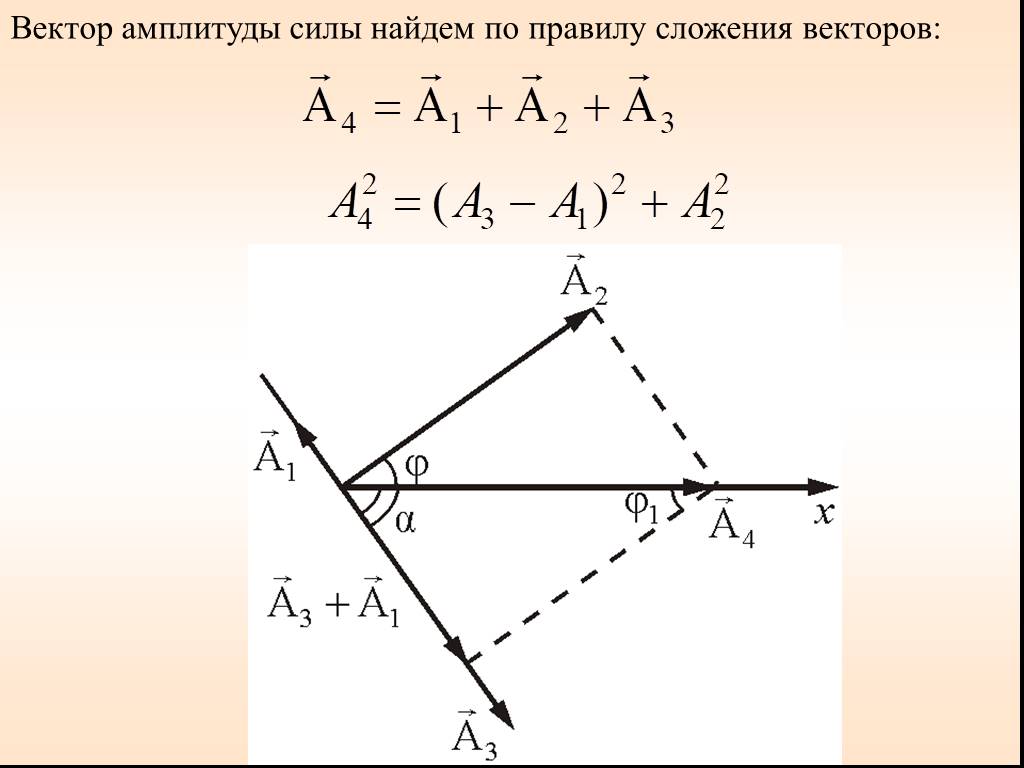
Сложение гармонических колебаний
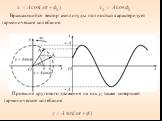
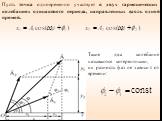
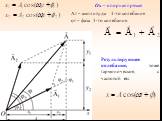
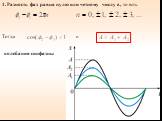
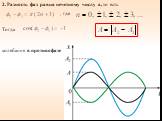
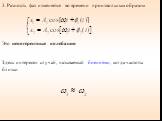
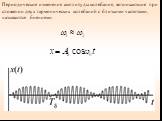
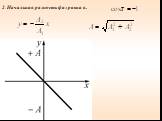
1. ВЕКТОРНАЯ ДИАГРАММА (I). Сложение гармонических колебаний одного направления облегчается и становится наглядным, если изображать колебания графически ...Уравнения трансформаторов
Принцип действия трансформатора и его уравнения. Определение трансформатора. Трансформатор — это статическое электромагнитное устройство, имеющее ...Свободные и вынужденные электромагнитные колебания. Колебательный контур. Период свободных электромагнитных колебаний
1. Электроёмкость. Конденсатор. Электроёмкость Обозначение: Единица измерения:. физическая величина, равная отношению заряда проводника к разности ...Наблюдение вынужденных электрических колебаний
Приборы и материалы. 1)Магнит дугообразный; 2)Катушка с железным сердечником от разборного электромагнита; 3)Миллиамперметр ; 4)Комплект проводов; ...Визуализация звуковых колебаний
Основные задачи :. проанализировать литературу по теме; создать установку для получения стоячих волн; исследовать, есть ли зависимость вида изображения ...Строение атома Квантовая физика
строение атома 11 квантовая физика ФИЗИКА КЛАСС. Данный урок проводится по типу телевизионной передачи…. Квантовая физика. Строения атома. ВЫХОД. ...«Световые волны» физика
Оглавление:. Принцип Гюйгенса Закон отражения света Закон преломления света Полное отражение Линза Расчёт увеличения линзы Дисперсия света Интерференция ...Радиосвязь физика
Вопросы. Что такое и колебательный контур? Для чего он предназначен Какие превращения энергии происходят в колебательном контуре? Чем отличается открытый ...Свободное падение физика
Свободное падение тел впервые исследовал Галилей, который установил, что свободно падающие тела движутся равноускоренно с одинаковым для всех тел ...Науки и физика
ИНТЕГРАЦИЯ — (лат. Integratio- восстановление-восполнение) процесс сближения и связи наук, состояние связанности отдельных частей в одно целое, а ...Презентации и физика
Актуальность. «Главная задача современной школы - это раскрытие способностей каждого ученика, воспитание личности, готовой к жизни в высокотехнологичном, ...Молекулярная физика
Цель: повторение основных понятий, законов и формул МОЛЕКУЛЯРНОЙ ФИЗИКИ в соответствии с кодификатором ЕГЭ. Элементы содержания, проверяемые на ЕГЭ ...Молекулярная физика и термодинамика
Содержание:. Структура и содержание МКТ. Основные положения МКТ. Опытные обоснования МКТ. Роль диффузии и броуновского движения в природе и технике. ...Квантовая физика
П Л А Н 1. СТО А. Эйнштейна. 2. Тепловое излучение. 3. Фотоэффект. 4. Люминесценция. 5. Химическое действие света. 6. Световое давление. 7. Физический ...«Оптические приборы» физика
Содержание. 1.Телескоп 2.Строение телескопа 3.Разновидности телескопов 4.Рефлекторы 5.Использование телескопов 6.Микроскоп 7.Создание микроскопа 8.Использование ...«МКТ» физика
Содержание. Молекулярная физика Основы молекулярно-кинетической теории строения вещества (МКТ) Температура и внутренняя энергия тела Характеристика ...«Механические волны» физика
Цель исследования: установить с научной точки зрения, что такое звук. Задачи исследования: 1. Изучить физическую теорию звука. 2. Исследовать историю ...«Давление твёрдых тел» физика
Физический диктант. Обозначение площади – Единица площади – Площадь прямоугольника – Обозначение силы – Единица силы – Формула силы тяжести – Обозначение ...Лампы накаливания физика
Актуальность. 2 июля 2009 года Президент России Дмитрий Медведев, выступая на заседании президума Госсовета по вопросам повышения энергоэффективности ...«Сообщающиеся сосуды» физика
Цель: изучить особенности сообщающихся сосудов и сформулировать основной закон сообщающихся сосудов. Опыт с двумя трубками. Опыт с сосудами разной ...Конспекты
Распространение колебаний в упругой среде. Поперечные и продольные волны
План-конспект урока физики в 9 классе. Тема урока:. "Распространение колебаний в упругой среде. Поперечные и продольные волны". . Подготовила: ...Распространение колебаний в упругой среде. Волновое движение. Продольные и поперечные волны. Длина волны. Скорость распространения волн. Свойства механических волн
15.01.2015. Тема : « Распространение колебаний в упругой среде. Волновое движение. Продольные и поперечные волны. Длина волны. Скорость распространения ...Период колебаний математического и пружинного маятников
Урок по теме. :. «Период колебаний математического и пружинного маятников». . . Цель урока: Добиться понимания и выработать начальные навыки по ...Распространение колебаний в среде. Волны. Продольные и поперечные волны
Тема:. . Распространение колебаний в среде. Волны. Продольные. и поперечные волны. Слайд №1. Тип урока:. урок изучения нового материала. № ...Исследование зависимости периода механических колебаний
Муниципальное общеобразовательное учреждение лицей. Региональная педагогическая мастерская по проблеме. «Ноосферология и образование». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 января 2019
Категория:Физика
Содержит:67 слайд(ов)
Поделись с друзьями:
Скачать презентацию