Презентация "Случайные величины: законы распределения" по физике – проект, доклад
Презентацию на тему "Случайные величины: законы распределения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Физические величины
Д.И.Менделеев. Наука начинается с тех пор, как начинают измерять. Портрет Менделеева в мантии профессора 1885 г . /Илья Ефимович Репин/. Автор работы: ...Уравнение состояния идеального газа. Газовые законы
Макроскопические параметры – это…:. Масса, давление, объем, температура. давление, объем, температура. Состояние газа данной массы характеризуется ...Физические величины
С древних времен людям приходилось измерять длину, отсчитывать время , взвешивать различные тела. Поэтому издавна употреблялись такие единицы, как ...Свет и его законы
Свет — электромагнитное излучение, испускаемое нагретым или находящимся в возбуждённом состоянии веществом, воспринимаемое человеческим глазом. Любой ...Сила и законы Ньютона
Первый закон Ньютона. Тело сохраняет состояние покоя до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Рисунки ...Основные понятия и законы динамики
Галилео Галилей (1564-1642). На основе экспериментальных исследований движения шаров по наклонной плоскости. Скорость любого тела изменяется только ...Основные понятия и законы электростатики
Электромагнитные силы – силы притяжения и отталкивания, возникающие между электрически заряженными частицами и телами. Электродинамика – раздел физики, ...Газовые законы
в 1662 г. Р. Бойлем; в 1676 г. Э. Мариоттом. Роберт Бойль. Закон Бойля-Мариотта. Эдм Мариотт. При постоянной температуре давление данной массы газа ...Газовые законы
Давайте вспомним. Какие величины характеризуют состояние макроскопических тел? Что называют уравнением состояния? ответы 1.давление - P, объем – V, ...Газовые законы
2013 Очер Бавкун Т.Н. Идеальный газ Исторические данные Закон Бойля – Мариотта Закон Шарля Закон Гей – Люссака Сводная таблица Разбор задачи на построение ...Газовые законы
Определение задач Изотермический процесс Изобарный процесс Изохорный процесс Домашнее задание Пример решения задачи. содержание. уравнение состояния ...Газовые законы
Изопроцессы Изотермический Изобарный Изохорный. Закон Бойля-Мариотта Постоянные температура и масса Переменные давление и объем. Изотермический процесс. ...газовые законы
Повторение. Перечислите основные положения МКТ. Дайте определение относительной молекулярной массы. Что такое количество вещества? Что такое молярная ...Газовые законы
Основные газовые законы. Закон Бойля-Мариотта: PV=const при t0=const Закон Шарля: P/T=const при V=const Закон Гей-Люссака: V/T=const при P=const ...Физические величины измерение физических величин
Физические величины: высота h , масса m, путь s, скорость v , время t, температура t, объём V и т.д. Измерить физическую величину – это значит сравнить ...Газовые законы (изопроцессы в газах)
Урок – путешествие по мотивам нартских сказаний. Тема урока: Решение задач. Цель: закрепить с учащимися знания газовых законов, уравнения состояния ...Алгоритм решения графических задач по теме "Газовые законы"
Дан график зависимости давления от температуры. Изобразить график этой зависимости в координатах P от V и V от T. Появление новых рисунков и записей ...Газы, газовые законы
Цели урока: 1. Закрепление знаний об идеальном газе, изопроцессах. 2. Формирование умений решения задач на применение уравнения состояния идеального ...Основные понятия и законы динамики
Относительность движения. Задание: Выяснить - в чём основное отличие геоцентрической и системы от гелиоцентрической? Аристотель 384 - 322 г. до н. ...Методы научного познания Физические величины
Что вы уже знаете? 1.Что такое физика? 2.Когда она возникла и где? 3.Для чего нужно изучать физику? 4.Что такое физическое тело? Приведите примеры. ...Конспекты
Физические величины и их измерение
Урок 2. Физические величины и их измерение. . . Цели урока:. . а) образовательные. ученик должен усвоить:. - понятие физической величины ...Физические явления и законы
Физические явления и законы. 1. На рисунке представлены графики зависимости смещения . x. грузов от времени . t. при колебаниях ...Молекулярная физика. Газовые законы
МОДЕКУЛЯРНАЯ ФИЗИКА. ГАЗОВЫЕ ЗАКОНЫ. (решение задач повышенной сложности). 10 класс. Учителя: Юдинцева Ольга Васильевна. ...Физические величины
Групповой урок в 7 классе тема «Физические величины». Задерко Елена Яковлевна. Учитель физики высшей категории. ГБОУ №365 Фрунзенского района. ...Изопроцессы. Газовые законы
Подробный конспект урока. . Организационная информация. Тема урока. . Изопроцессы. Газовые законы. . . Предмет. . Физика. . ...Изопроцессы. Газовые законы
Тема урока:. "Изопроцессы. Газовые законы". Цели урока:. Создать условия по изучению изопроцессов термодинамических параметров, графики изопроцессов, ...Изопроцессы и их законы
МОБУ «Хрущевская СОШ им. А.И. Миронова». УРОК ФИЗИКИ. по теме. «Изопроцессы и их законы». для 10 класса. Учитель: Сорокина Е.В. ...Газовые законы и их применение
ИНТЕГРИРОВАННОЕ ЗАНЯТИЕ ПО ФИЗИКЕ. Учитель физики Бахчисарайской ОШ № 4, Республика Крым:. . Марынич Н.Н. Тип занятия. : комбинированный. Тема ...Газовые законы
Урок разработан Соловьевой Н.Н.,. учителем физики МБОУ «Спешковская ООШ». Очерского района Пермского края. Тема урока: «. Газовые законы». ...Газовые законы
Открытый урок по физике. . «Газовые законы». 10 класс. Учитель Касьянова Майя Валентиновна. Тип урока: . урок изучения и первичного закрепления ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 октября 2018
Категория:Физика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию



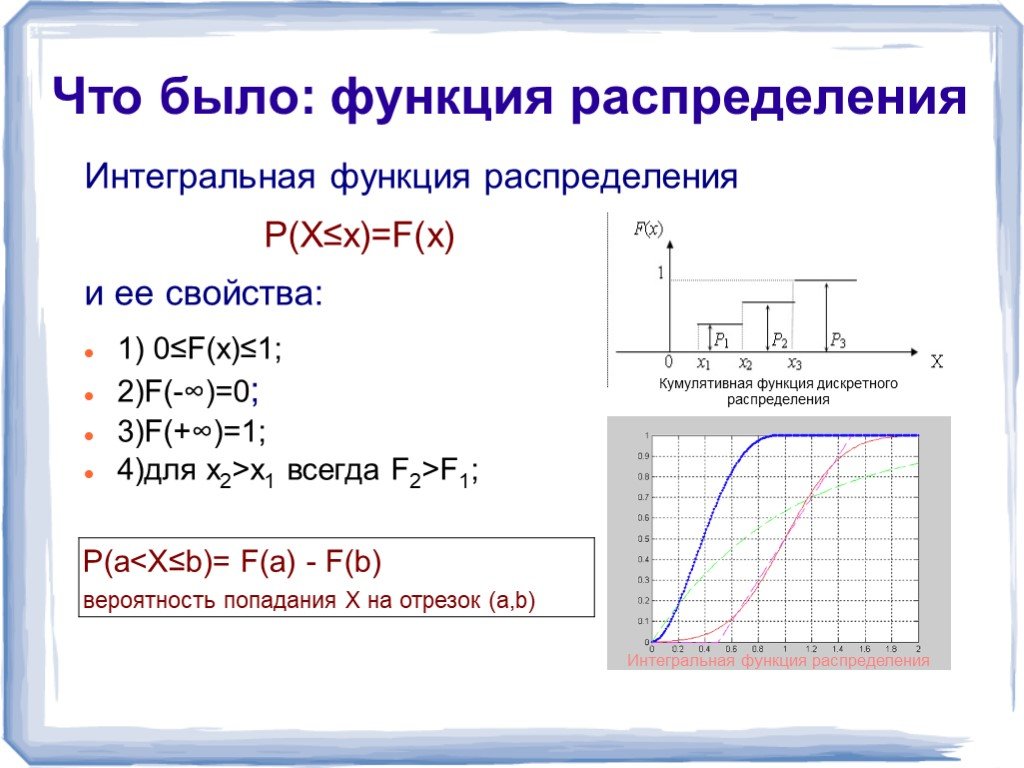














![Характеристики функции распределения. Дискретная случайная величина Математическое ожидание: М[x]= Дисперсия D[x]= Мода (значение с наибольшей вероятностью) Мо=Xi | p(xi)=pmax Медиана. Непрерывная случайная величина Математическое ожидание: M[X]= Дисперсия D[X]= Мода (значение с наибольшей плотность Характеристики функции распределения. Дискретная случайная величина Математическое ожидание: М[x]= Дисперсия D[x]= Мода (значение с наибольшей вероятностью) Мо=Xi | p(xi)=pmax Медиана. Непрерывная случайная величина Математическое ожидание: M[X]= Дисперсия D[X]= Мода (значение с наибольшей плотность](https://prezentacii.org/upload/cloud/18/10/80323/images/thumbs/screen5.jpg)


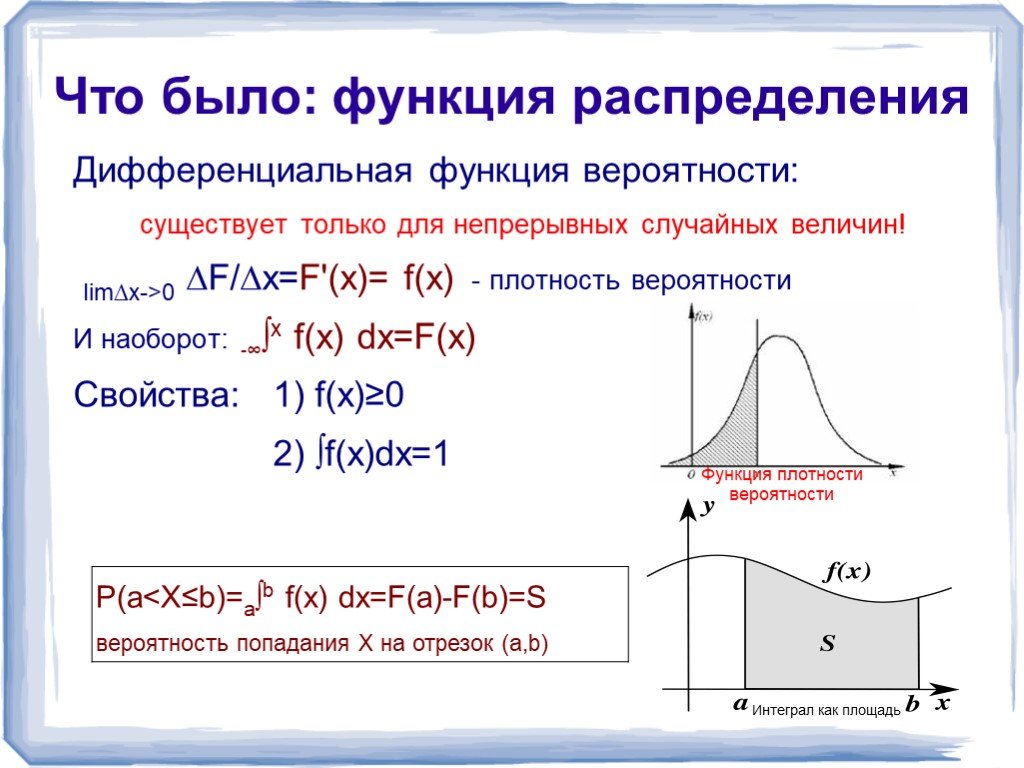
![Равномерное распределение №1. Непрерывная случайная величина имеет равномерный закон распределения на (а,b), если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его. Функция P(Xb Математическое ожидание: M[x]=(a+b)/2 Дисперсия: D[x]=(b-a)2/12. График интегральной функции распределе Равномерное распределение №1. Непрерывная случайная величина имеет равномерный закон распределения на (а,b), если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его. Функция P(Xb Математическое ожидание: M[x]=(a+b)/2 Дисперсия: D[x]=(b-a)2/12. График интегральной функции распределе](https://prezentacii.org/upload/cloud/18/10/80323/images/thumbs/screen8.jpg)
![Равномерное распределение №2. Дискретная случайная величина имеет равномерное распределение, если ее функция вероятности на всей области определения (a,b) имеет вид P(x)=1/n, где n — число исходов M[x]=(a+b)/2 - мат.ожидание D[x]=(n2-1)/12 - дисперсия. График кумулятивной функции. График характерист Равномерное распределение №2. Дискретная случайная величина имеет равномерное распределение, если ее функция вероятности на всей области определения (a,b) имеет вид P(x)=1/n, где n — число исходов M[x]=(a+b)/2 - мат.ожидание D[x]=(n2-1)/12 - дисперсия. График кумулятивной функции. График характерист](https://prezentacii.org/upload/cloud/18/10/80323/images/thumbs/screen9.jpg)
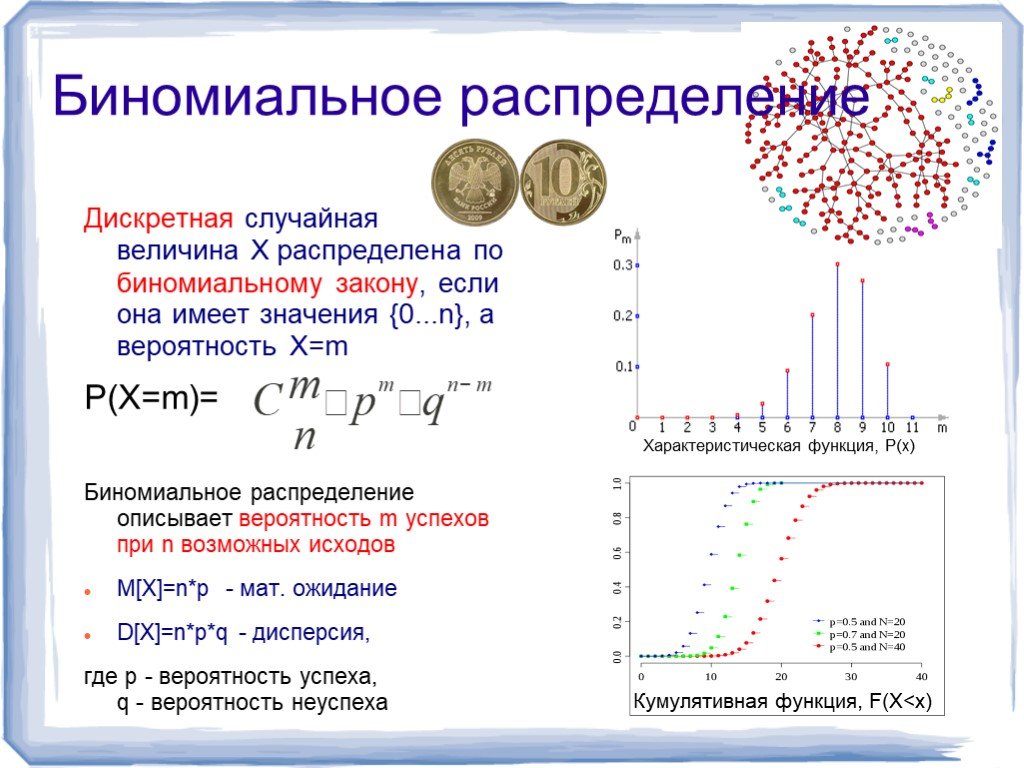
![Характеристическая функция, P(x). Биномиальное распределение. Дискретная случайная величина X распределена по биномиальному закону, если она имеет значения {0...n}, а вероятность Х=m P(X=m)= Биномиальное распределение описывает вероятность m успехов при n возможных исходов M[X]=n*p - мат. ожидание D Характеристическая функция, P(x). Биномиальное распределение. Дискретная случайная величина X распределена по биномиальному закону, если она имеет значения {0...n}, а вероятность Х=m P(X=m)= Биномиальное распределение описывает вероятность m успехов при n возможных исходов M[X]=n*p - мат. ожидание D](https://prezentacii.org/upload/cloud/18/10/80323/images/thumbs/screen10.jpg)
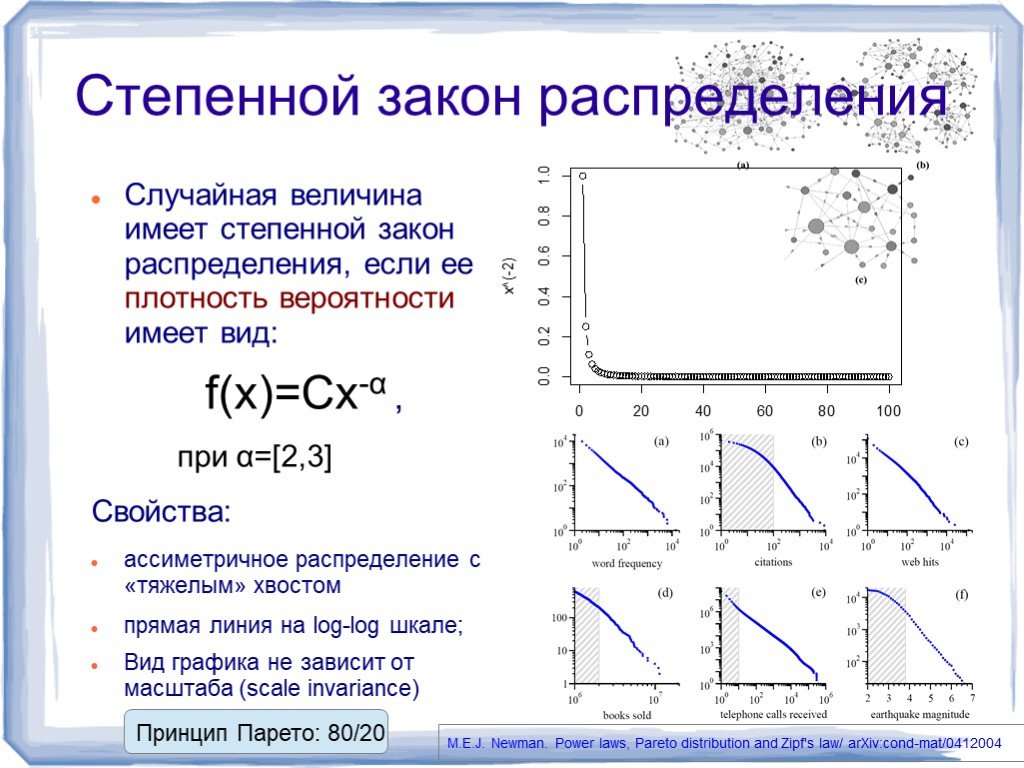
![Степенной закон распределения. Случайная величина имеет степенной закон распределения, если ее плотность вероятности имеет вид: f(x)=Cx-α , при α=[2,3] Свойства: ассиметричное распределение с «тяжелым» хвостом прямая линия на log-log шкале; Вид графика не зависит от масштаба (scale invariance). Прин Степенной закон распределения. Случайная величина имеет степенной закон распределения, если ее плотность вероятности имеет вид: f(x)=Cx-α , при α=[2,3] Свойства: ассиметричное распределение с «тяжелым» хвостом прямая линия на log-log шкале; Вид графика не зависит от масштаба (scale invariance). Прин](https://prezentacii.org/upload/cloud/18/10/80323/images/thumbs/screen11.jpg)





































