Презентация "Энергия" по физике – проект, доклад
Презентацию на тему "Энергия" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 71 слайд(ов).
Слайды презентации
Список похожих презентаций
Законы постоянного тока. Энергия конденсаторов
Закон сохранения электрического заряда. Справедлив для замкнутой системы зарядов. Сумма зарядов алгебраическая, то есть с учетом знаков зарядов. Конденсатор ...Энергия топлива. Удельная теплота сгорания топлива
№1 ВЫПИСАТЬ ВЕЩЕСТВА, КОТОРЫЕ ЯВЛЯЮТСЯ ТОПЛИВОМ. Нефть Природный газ Каменный уголь Древесина Табак Лампадное масло Вода Железо Порох. ТОПЛИВО – ВЕЩЕСТВО, ...Энергия фотоэффекта
Из истории фотоэффекта…. 1887 год – немецкий физик Генрих Герц. Второе открытие фотоэффекта. 1888 год – немецкий ученый Вильгельм Гальвакс. Третье ...Энергия топлива
Где используется топливо? Транспорт Промышленность Сельское хозяйство Быт. Что такое топливо? Топливо – вещества с высоким содержанием углерода: уголь, ...Энергия сгорания топлива
Удельная теплота сгорания топлива — физическая величина, показывающая, какое количество теплоты выделяется при полном сгорании топлива массой 1 кг ...Энергия солнца
Используемые в настоящий момент источники энергии (нефть, газ, уголь) ограничены и быстро сокращаются. Солнце является неисчерпаемым и экологически ...Энергия
Энергия. Энергия – скалярная физическая величина, характеризующая способность тел совершать работу. Энергия измеряется в джоулях. механическая внутренняя ...Энергия
Слово «энергия» употребляется нередко и в быту.Так, например, людей, которые могут быстро выполнять большую работу, называют энергичными, обладающими ...Электроёмкость Конденсатор Энергия конденсатора
Цели урока:. Сформировать понятия электрической ёмкости, единицы ёмкости; Вычислить энергию конденсатора; Рассмотреть различные соединения конденсаторов. ...Электроемкость. Конденсаторы. Энергия электростатического поля
Рассмотрим уединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов. Его потенциал, согласно ( ), прямо пропорционален ...Физика Энергия топлива
Тема: Энергия топлива. 8 класс. Вопросы на повторение:. 1. Что является источником энергии, которая используется в промышленности, на транспорте и ...Решение задач. Энергия топлива
Эпиграф. «Я мыслю, следовательно, я существую» Рене Декарт (Французский философ и математик 1590-1650). Цель урока: обобщить знания по теме «Энергия ...Мячи Взаимодействие Энергия
Прыгнем выше головы? h1 mgh1=mgh2+Q. h1=h2 h2 g. h0 t=2D/u=10x0,01/300=0,0003с D=5cм U=300м/с. h= 2gh0 t = 0,1мм h. ЗСЭ (m1+m2)gh0= m1gh1(t)+ m2gh2(t). ...Энергия связи ядра и дефект масс
Дефект масс Мя126C Мя=12 а.е.м. mp=1,00759 а.е.м. mn=1,00897 а.е.м. 6·mp+6·mn=6·(1,00759 а.е.м. +1,00897 а.е.м.)=12,09936 а.е.м. 12. m=(Z·mp+(A-Z)·mn) ...Энергия
Цель урока. - ввести понятия кинетической потенциальной и полной энергии как характеристик механических систем. Механическая энергия — это энергия, ...Энергия связи. Дефект масс
Ядерные силы. самые могучие из всех, которые мы знаем на сегодняшний день. Они не только почти полностью подавляют взаимную антипатию протонов, которая ...Энергия & Люди
Содержание Уголь. Нефть и природный газ. Нетрадиционные топливные источники. Атом и Вода. Энергетика России. Виды энергии. Альтернативные источники ...Энергия солнца
План исследования. Опрос «Энергия солнца в вашем доме» В чем заключается энергия солнца? Солнечная энергия до нашего времени. Солнечная энергия сегодня. ...Энергия атома: за и против
Так не бывает, чтобы экспериментаторы вели свои поиски ради открытия нового источника энергии или ради получения редких или дорогих элементов. Истинная ...Конспекты
Ядерные реакции. Энергия связи. Дефект масс
МБОУ «Учхозская средняя общеобразовательная школа» Краснослободского муниципального района Республики Мордовия. Конспект урока по информатике в ...Ядерные силы. Энергия связи нуклонов в ядре, дефект массы
Урок № 61-169 Ядерные силы. Энергия связи нуклонов в ядре, дефект массы. . Ядерные. . реакции. Изотопы. . . Ядерные силы – силы, действующие ...Энергия связи ядер. Цепные реакции
Тема урока: Решение задач «Энергия связи ядер. Цепные реакции». 11 класс. Учитель: Каменцева О.Н. 20.02.14 г. Цели урока:. обобщить и систематизировать ...Энергия топлива.Удельная теплота сгорания топлива
Муниципальное бюджетное образовательное учреждение. средняя общеобразовательная школа №3 г.Навашино. Нижегородской области. ...Энергия
Муниципальное бюджетное образовательное учреждение. «Авнюгская средняя общеобразовательная школа». Верхнетоемского района Архангельской области. ...Энергия
Синквейн - Составная часть урока. . Воронкова Екатерина Валерьевна. учитель физики, ГОУ СОШ № 1388 г. Москвы. Класс:. 10, 11 класс. Тип урока:. ...Электроемкость. Единицы емкости. Конденсаторы. Энергия заряженного конденсатора. Применение конденсаторов
Тема урока:. . Электроемкость. Единицы емкости. Конденсаторы. Энергия заряженного конденсатора. Применение конденсаторов. Цель:. 1. . Дать понятие ...Электромагнитная индукция, самоиндукция, индуктивность. Энергия магнитного поля
Урок по теме «Электромагнитная индукция, самоиндукция, индуктивность. . . Энергия магнитного поля». 11 класс. Цель урока:. . Обобщить знания, ...Электрическая емкость. Конденсатор. Энергия электрического поля конденсатора
№__________сабақтың жоспары. План урока №___________________. Сабақтың тақырыбы:. . Тема урока. :. Электрическая емкость. Конденсатор. Энергия ...Удельная теплота сгорания. Энергия топлива
Удельная теплота сгорания. Энергия топлива. Цель урока:. Изучить вопросы использования внутренней энергии топлива, выделения тепла при сгорании ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 февраля 2019
Категория:Физика
Содержит:71 слайд(ов)
Поделись с друзьями:
Скачать презентацию

















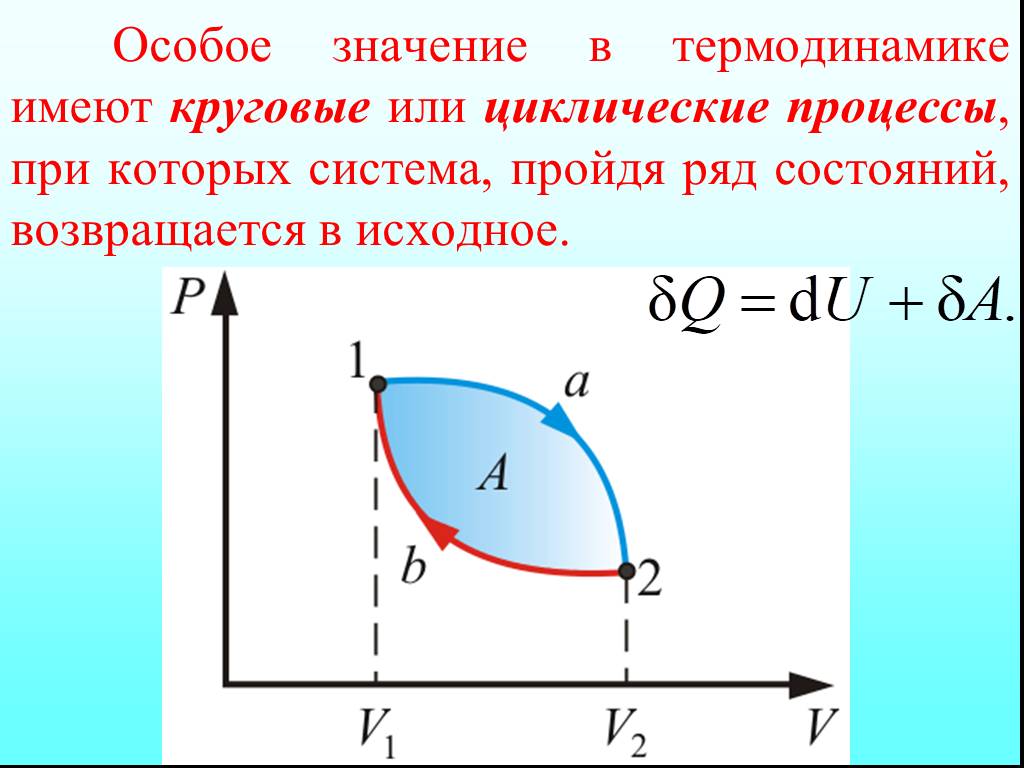





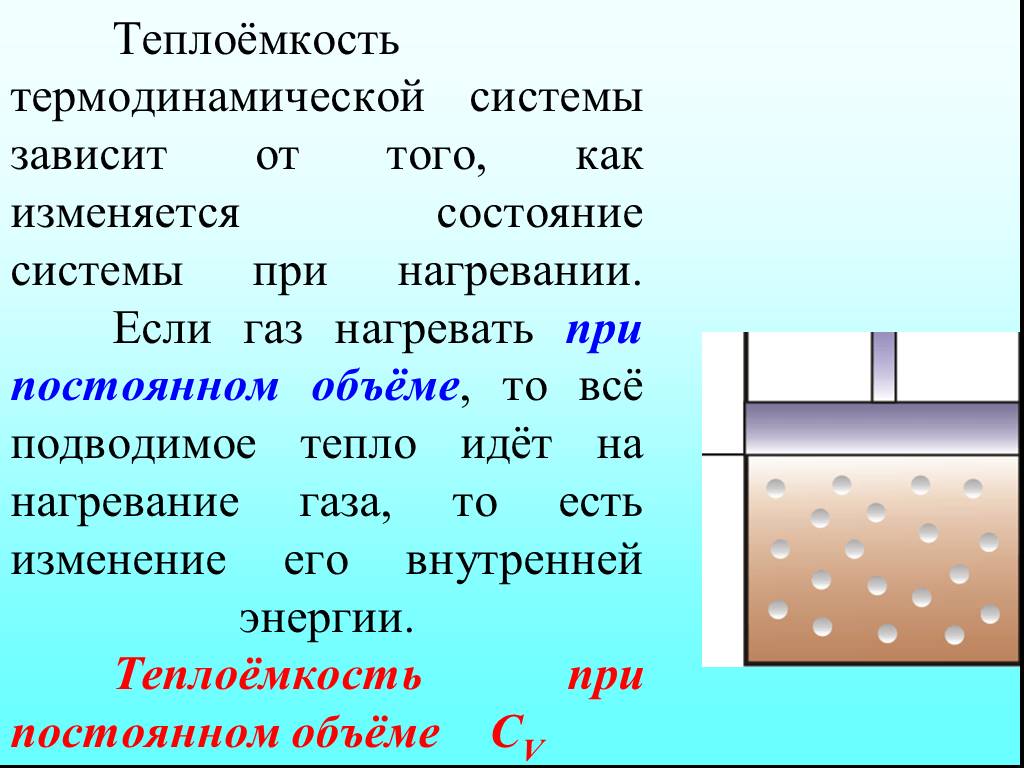
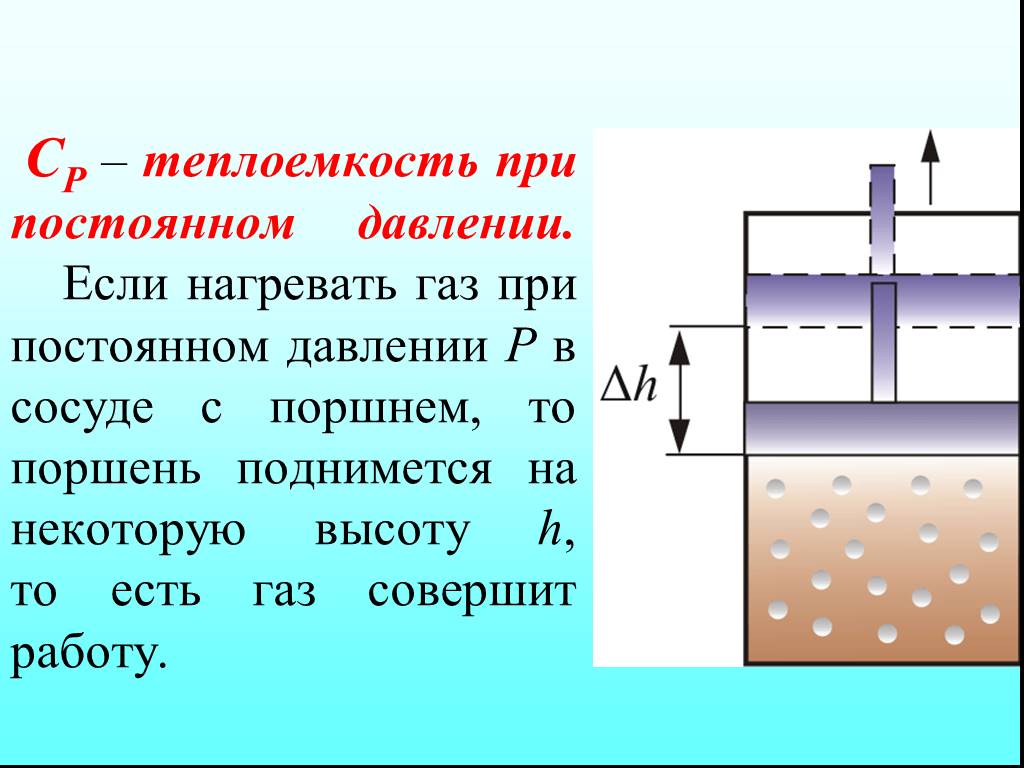







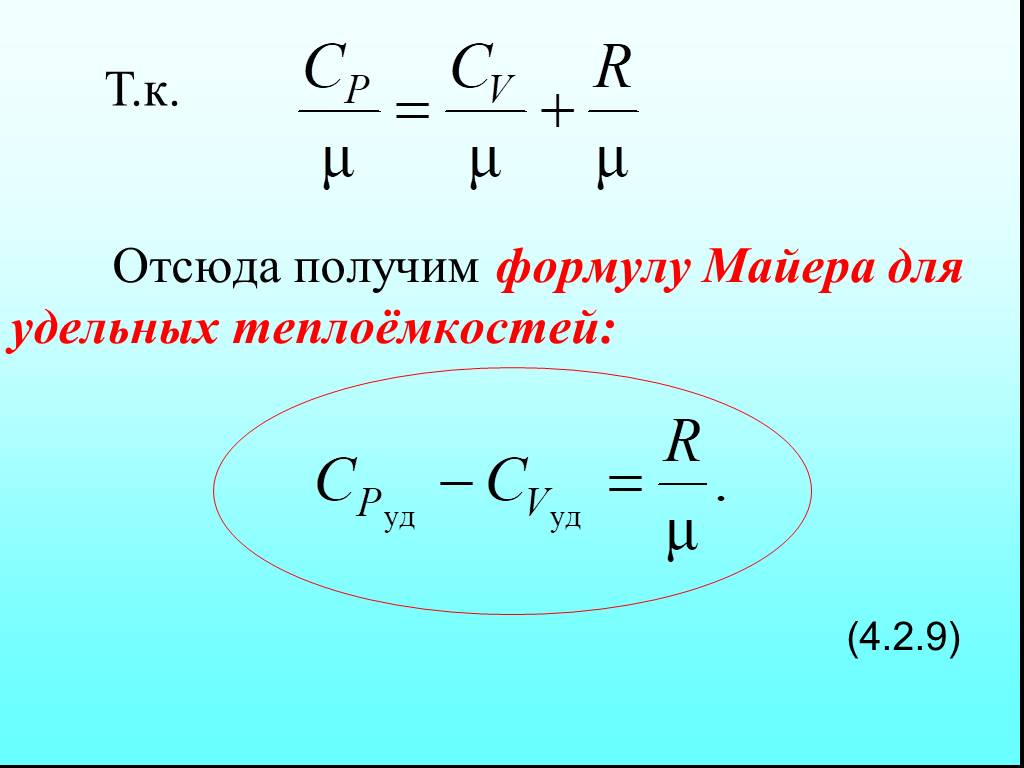




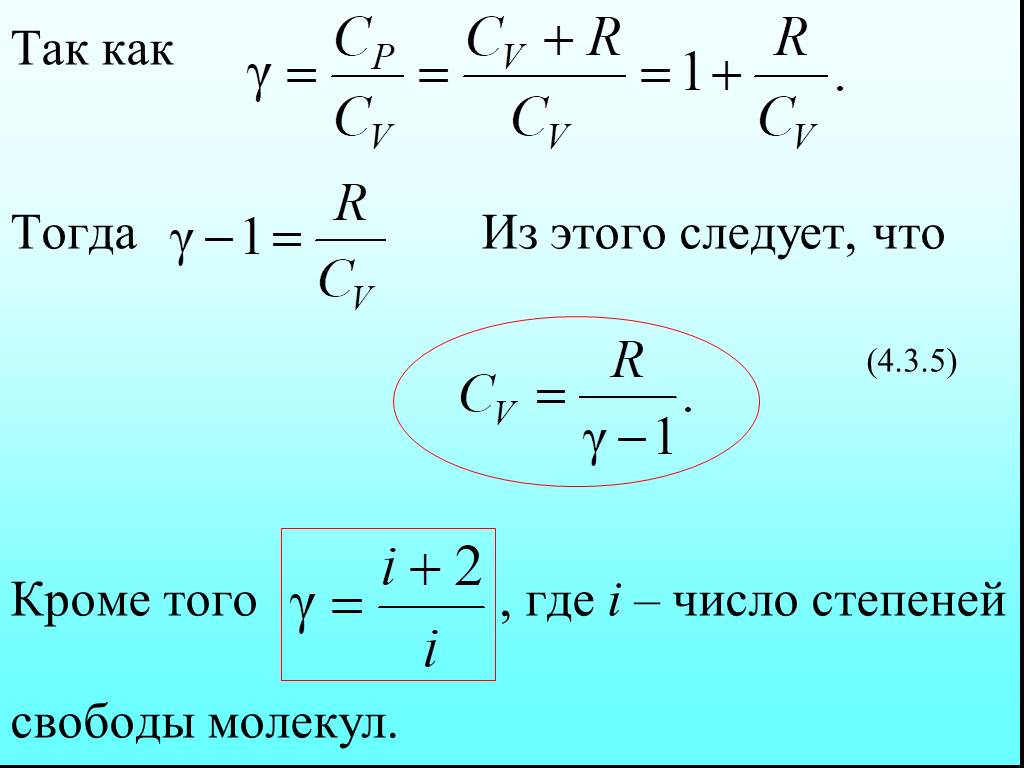























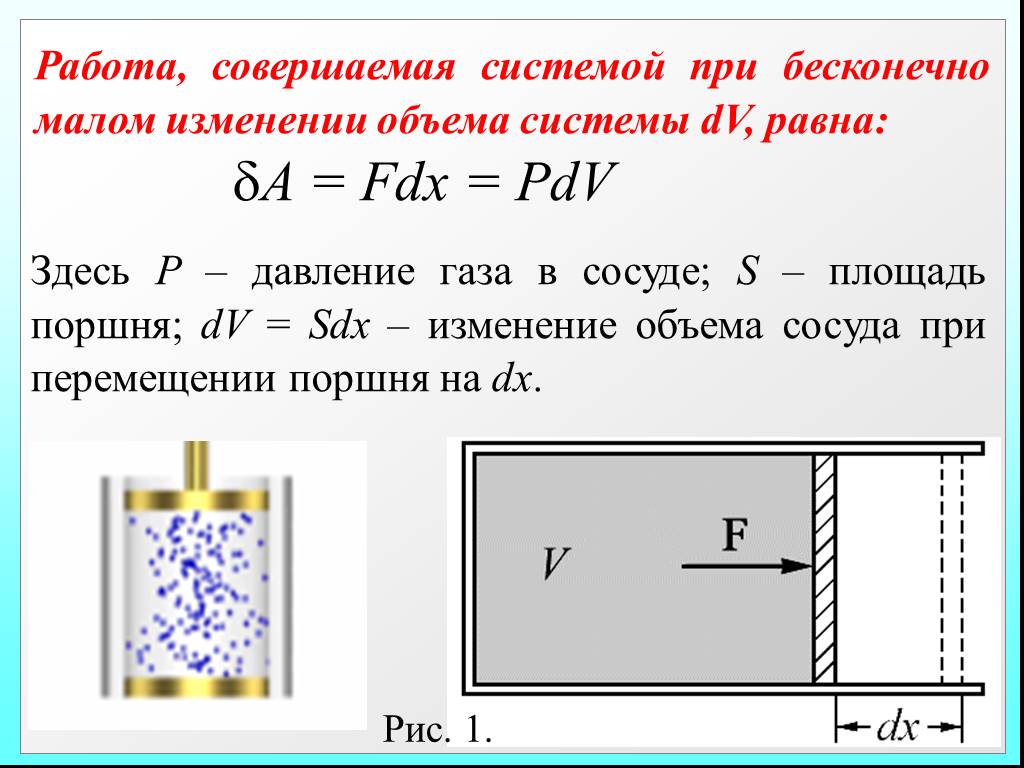


















![4.2. Теплоёмкость идеального газа. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус (4.2.1) Размерность теплоемкости: [C] = Дж/К. Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости. 4.2. Теплоёмкость идеального газа. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус (4.2.1) Размерность теплоемкости: [C] = Дж/К. Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.](https://prezentacii.org/upload/cloud/19/02/122756/images/thumbs/screen20.jpg)
![Удельная теплоёмкость Суд – есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Сμ количество теплоты, необходимое для нагревания 1 кмоля газа на 1 градус (4.2.2) [Cμ] = Дж/(мольК). Удельная теплоёмкость Суд – есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Сμ количество теплоты, необходимое для нагревания 1 кмоля газа на 1 градус (4.2.2) [Cμ] = Дж/(мольК).](https://prezentacii.org/upload/cloud/19/02/122756/images/thumbs/screen21.jpg)