Класс: 5Б
Предмет: математика
Учебник: Наглядная геометрия 5-6 классы
Авторы: И.Ф.Шарыгин; Л.Н.Ерганжиева. Москва: Дрофа 20 13 г.
Продолжительность занятия: 40 мин
Оборудование: Компьютер, проектор, документ-камера, электронная презентация из 8 слайдов с видеороликом с физкультминуткой, макет жука, раздаточный материал (бумажные полоски 5*28 см, клей, ножницы, таблица для фиксирования результатов опытов), карточки с терминами.
Технологическая карта факультативного занятия
Тема факультативного занятия: Топологические опыты
Цель для ученика: узнать про понятие «Топология», познакомиться и осуществить топологические опыты
Цель для учителя: Формировать представление понятия «Топология» как части геометрии; познакомить обучающихся с топологическими опытами на практике. Задачи: Образовательные: (формирование познавательных УУД) : выявлять особенности разных объектов в процессе их рассматривания; выделение общего и различного в изучаемых объектах, классификация объектов; применять модели для получения информации Воспитательные: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, организовывать и планировать учебное сотрудничество с учителем и сверстниками, (формирование коммуникативных и личностных УУД) Развивающие (формирование регулятивных УУД ) умение обрабатывать информацию и ранжировать ее по указанным основаниям, представлять информацию в табличной форме. |
| Тип занятия: первичное предъявление новых знаний.
| Форма занятия: лаборатория геометрических открытий |
| Опорные понятия, термины Математика; Геометрия; Арифметика Прямоугольник; Круг; Кольцо | Новые понятия: Топология; траектория движения; Односторонняя поверхность; Перекрученное кольцо ( Лист Мебиуса) |
| Этап урока и его цели | Деятельность педагога | Деятельность обучающихся | Формируемые УУД |
-
Оргмомент
| Приветствует учащихся | Приветствуют присутствующих | Коммуникативные УУД |
-
Актуализация знаний учащихся.
Постановка целей и задач занятия. | Проводит фронтальный опрос по понятиям : математика, геометрия; организует постановку учащимися целей и задач урока. | Строят речевые высказывания; формулируют цель и задачи урока | Коммуникативные и регулятивные УУД |
-
Основная часть
Первичное осмысление и закрепление знаний | Организует групповую работу обучающихся через проведение математических опытов для ознакомления с новым материалом | Договариваются о совместной деятельности, проводят опыты, приходят к общему решению | Коммуникативные УУД (Формирование умения участвовать в коллективном обсуждении проблем, организовывать и планировать учебное сотрудничество с учителем и сверстниками); Познавательные УУД (Формирование умения выделять особенности разных объектов в процессе их рассматривания; классифицировать понятия); Регулятивные УУД (формирование умения вносить необходимые дополнения и коррективы в план собственных действий в случае расхождения результата с эталоном); Личностные УУД
(Формирование интереса к познавательной деятельности, умения слушать и вступать в диалог).
|
-
Физкультминутка
| Показывает ребятам видеоролик с физкультминуткой | Выполняют упражнения за веселым человечком | Личностные УУД (формирование мотивации к самосовершенствованию); Коммуникативные УУД (умение управлять своим поведением).
|
-
Закрепление изученного.
| Организует групповую работу обучающихся через проведение математических опытов для закрепления нового материала | Закрепляют полученные знания на практике, заполняют предложенную таблицу. | Познавательные УУД (Формирование умения выделять общее и различное в изучаемых объектах, применять модели для получения информации) Коммуникативные УУД (Участвовать в коллективном обсуждении проблем); Регулятивные УУД (Умение обрабатывать информацию и ранжировать ее по указанным основаниям, представлять информацию в табличной форме).
|
-
Заключительная часть
| Рассказывает о применении листа Мебиуса в различных областях человеческой деятельности, объявляет тему проекта: «Лист Мебиуса» Организует подведение итогов и самооценивание учащихся. | Формируют и высказывают свои предположения. Оценивают себя | Личностные УУД (формирование навыков самооценки); Коммуникативные УУД (Умение слушать и вступать в диалог)
|
| Задание по проектной деятельности Подведение итогов Рефлексия |
Математика-


Лента Мёбиуса — поверхность с одной стороной и одним краем; пример объекта, изучаемого в топологии
Тополо́гия (от др.-греч. τόπος — место и λόγος — слово, учение) — раздел математики, изучающий в самом общем виде явление непрерывности, в частности свойства пространства, которые остаются неизменными при непрерывных деформациях, например, связность, ориентируемость. В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов (например, расстояние между парой точек). Например, с точки зрения топологии, кружка и бублик (полноторий) неотличимы.
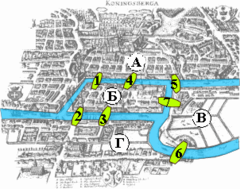

Семь мостов Кёнигсберга — одна из первых задач топологии, рассмотренная Эйлером
Раздел математики, который мы теперь называем топологией, берет свое начало с изучения некоторых задач геометрии. Различные источники указывают на первые топологические по духу результаты в работах Лейбница и Эйлера, однако термин «топология» впервые появился в 1847 году в работе Листинга. Листинг определяет топологию так:
Под топологией будем понимать учение о модальных отношениях пространственных образов, или о законах связности, взаимного положения и следования точек, линий, поверхностей, тел и их частей или их
совокупности в пространстве, независимо от отношений мер и величин[1]
Когда топология еще только зарождалась (XVIII—XIX века), её называли геометрия размещения (лат. geometria situs) или анализ размещения (лат. analysis situs). Приблизительно с 1925 по 1975 годы топология являлась сильно развивающейся отраслью в математике.
Общая топология зародилась в конце XIX в. и оформилась в самостоятельную математическую дисциплину в начале XX в. Основополагающие работы принадлежат Хаусдорфу, Пуанкаре, Александрову, Урысону, Брауэру.
Матема́тика (от др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов[
Математика… наука о количественных отношениях и пространственных формах действительного мира.


![]()

![]()
