Конспект урока «Решение задач с помощью уравнений» по математике
Тема: Решение задач с помощью уравнений (2 урока)
Цели: выработать навыки решения уравнений и задач методом составления уравнения, развивать вычислительные навыки, логическое мышление учащихся, быстроту реакции, умение ориентироваться в различных ситуациях, приближенных к жизни.
Этапы урока
-
Организационный момент. Объявление темы урока, плана, целей и задач. (2 мин)
-
Разминка. Комментированное решение уравнений. Повторение правила переноса слагаемых из одной части уравнения в другую (8 мин.)
-
Самостоятельная работа «Решение уравнений» (15 мин)
-
Новый материал (15 мин.)
-
Самостоятельное решение задач (работа в группах) (35 мин)
-
Подведение итогов, домашнее задание (5 мин).
Ход урока
-
Прокомментировать решение уравнений:
-
0,6у + 4 = 0,2у
-
1,3 ─ 0,6с = 0,2 ─ 0,5с
-
- х ─ 1,4 = 0,4х
-
7 ─ 6,4х = 3,6х.
-
-
Самостоятельная работа «Решение уравнений».
Вариант 1.
-
4,37 +6,7x = 7,75 + 9,3x; 1 балл
-
4(3─ x) ─ 11 = 7(2x ─ 5); 1 балл
-
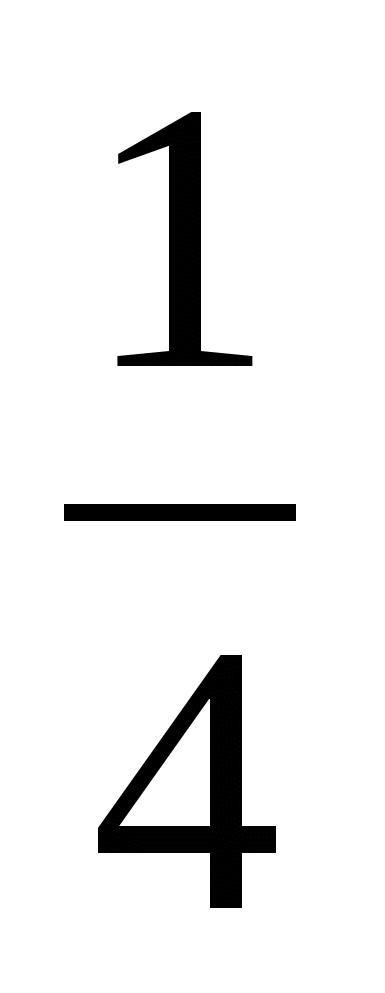 ─
─ 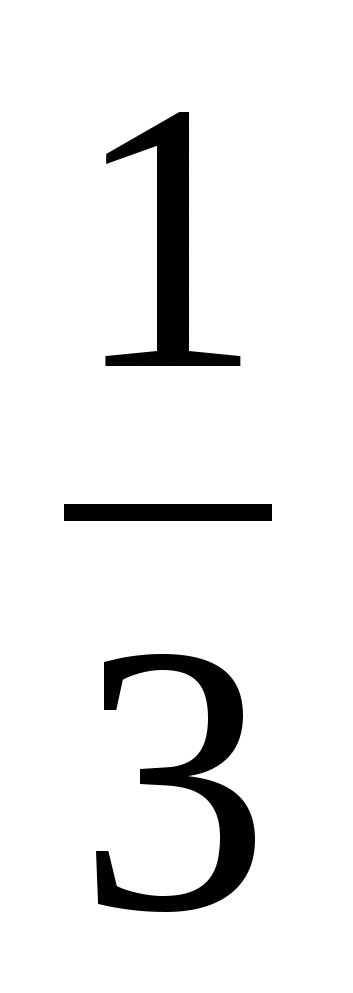 m =
m = 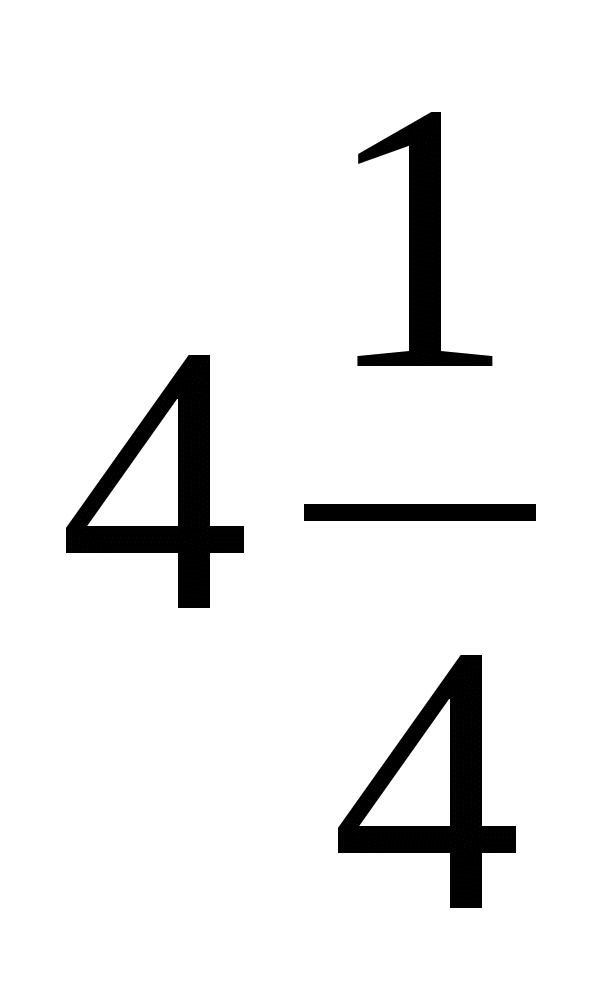 ─3m; 2 балла
─3m; 2 балла -
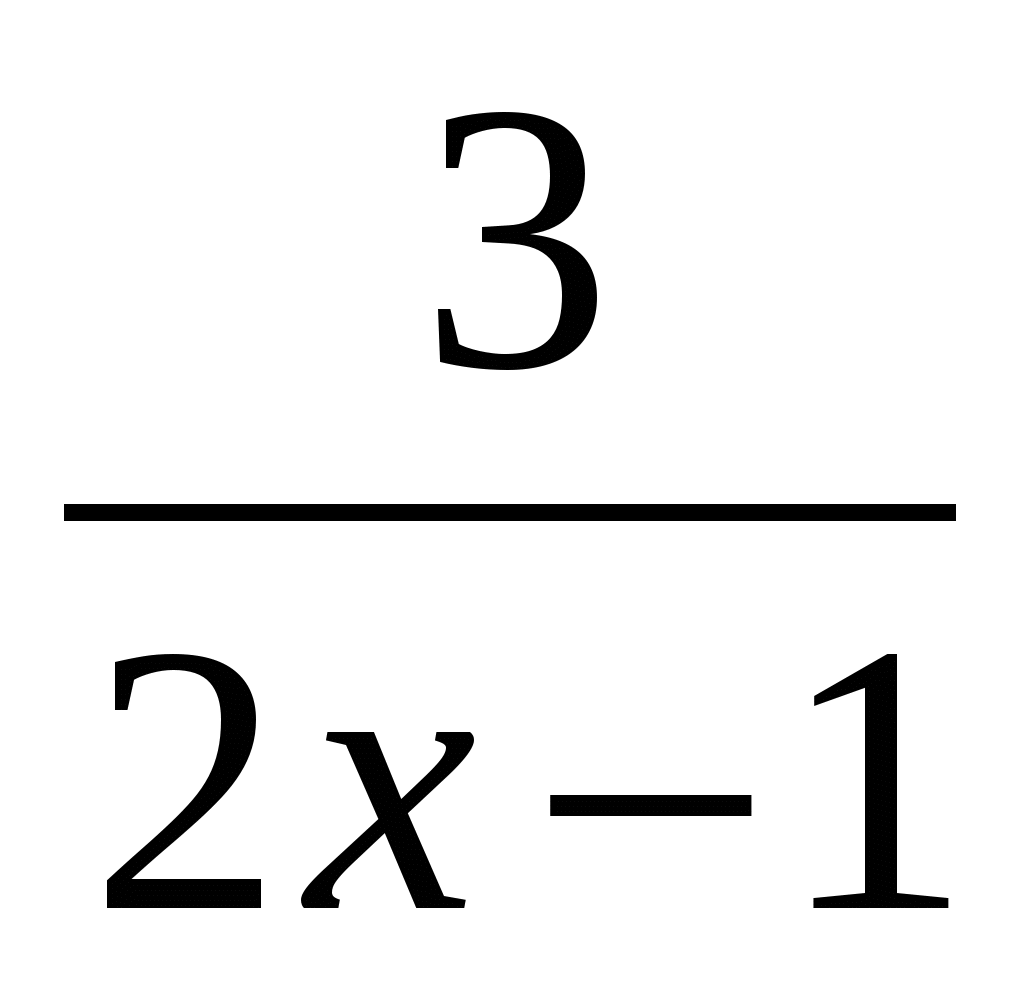 =
= 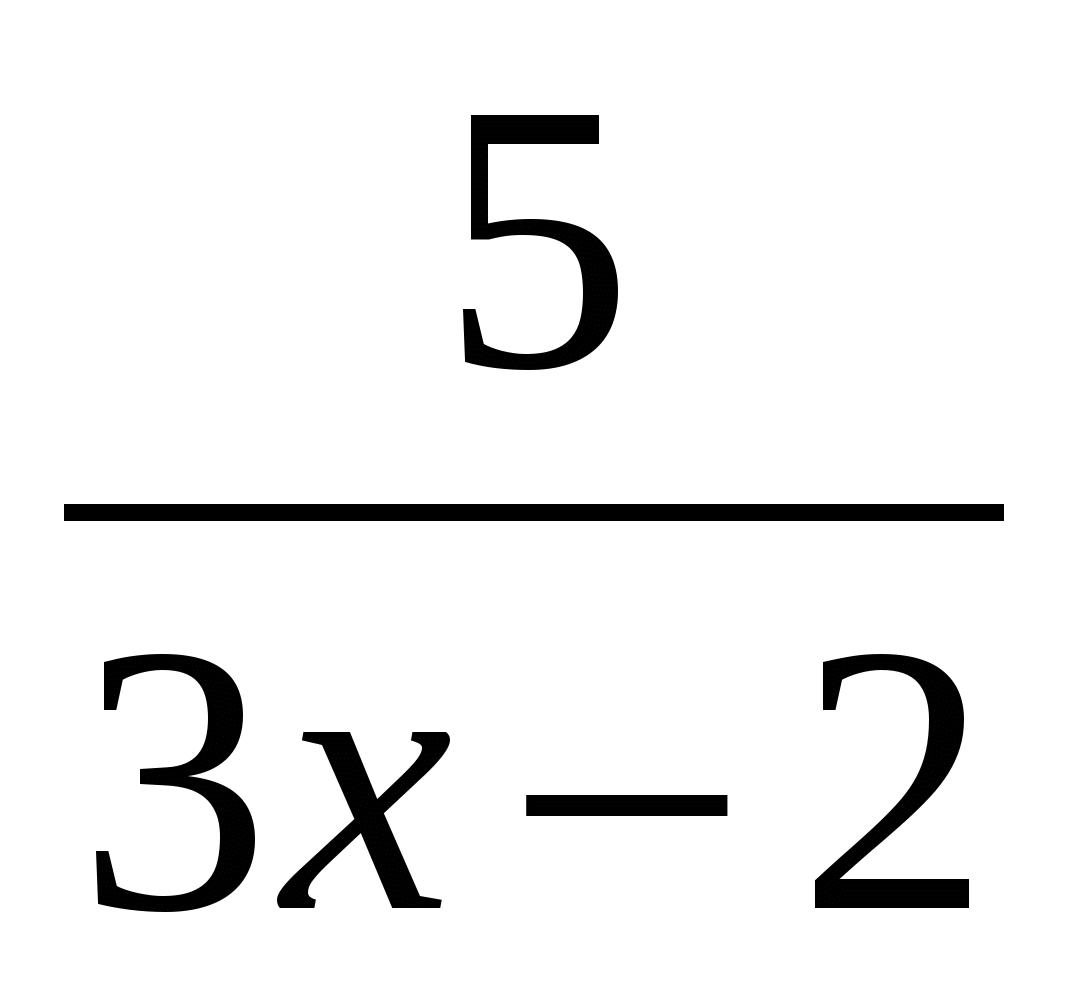 . 2 балла
. 2 балла
Вариант 2.
-
1) 8,9x +17,54 = 5,4x + 2,84; 1 балл
-
2) 3(5─ x) + 13 = 4(3x ─ 8); 1 балл
-
3)
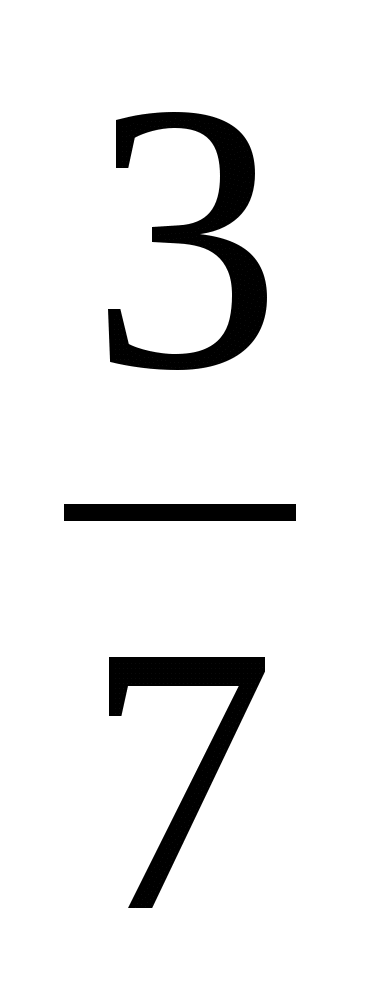 ─
─ 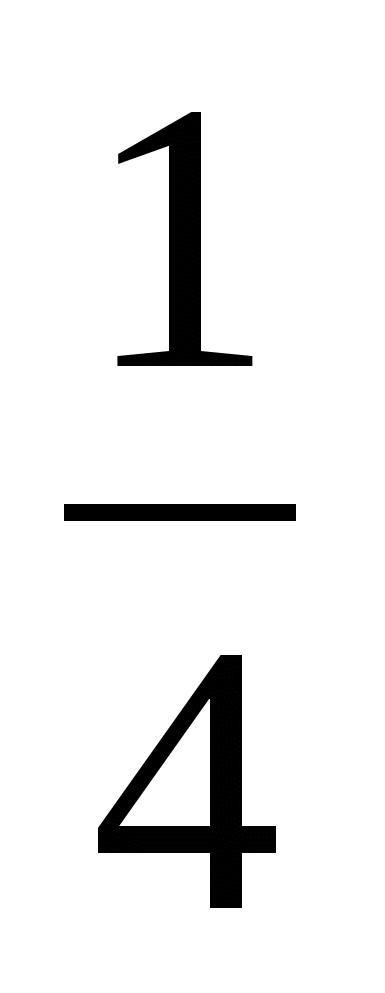 n =
n = 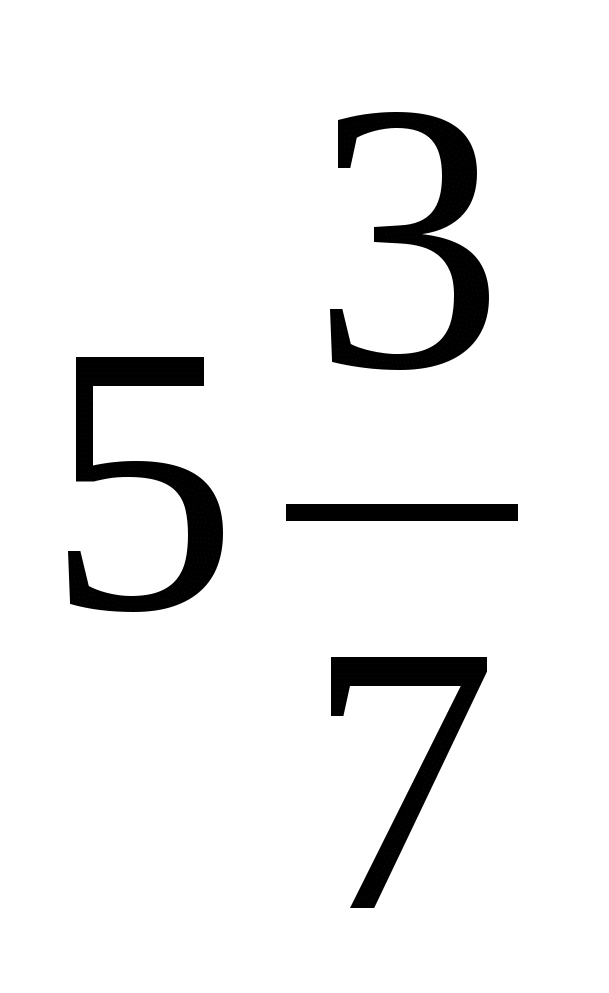 ─ 4n; 2 балла
─ 4n; 2 балла
4) ![]() =
= ![]() . 2 балла
. 2 балла
Вариант 3.
1) ─ 3(2x ─0,8) = 2(x + 3,6); 1 балл
2) ![]() ─1,27 =
─1,27 = ![]() ─ 4,77; 2 балла
─ 4,77; 2 балла
3) ![]() =
= ![]() ; 2 балла
; 2 балла
4)* При каком значении а уравнение (а ─ 2)∙x = 1 не имеет корней? 2 балла
-
Новый материал.
С помощью уравнений можно решать многие задачи. Для этого нужно (учащиеся вспоминают):
-
неизвестную величину обозначить буквой;
-
используя условие задачи, составить уравнение;
-
решить составленное уравнение;
-
ответить на вопрос задачи.
Задание 1.
Составь задачу, которую можно решить с помощью данного уравнения:
-
х + (х + 5) = 94
-
6х ─ х = 20;
-
7х + х = 24;
-
(34 ─ х) ─ х = 2.
Задание 2.
Задача 1. Старик за два дня поймал 13,1 кг рыбы, причем в первый день поймал рыбы на ![]() кг меньше, чем во второй день. Сколько рыбы поймал старик в первый день?
кг меньше, чем во второй день. Сколько рыбы поймал старик в первый день?
Составь схему и уравнение к задаче.
Решение:
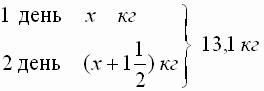
Задача 2. Найдите число, ![]() которого равны 12.
которого равны 12.
Задача 3. Мама в 6 раз старше сына, а сын на 25 лет младше мамы. Сколько лет маме?
Задача 4. Лодка за 0,3 часа по течению реки проплывет такой же путь, что и за 0,5 часа против течения. Какова собственная скорость лодки, если скорость течения реки 2,1 км/ч?
Задача 5. На солнышке грелись несколько кошек. У них вместе лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
-
Задачи для самостоятельного решения.
1 уровень.
1. Одно число в 5 раз больше другого, а их сумма равна 42. Найди неизвестные числа (1 балл).
2. Одно число в 7 раз больше другого, а их разность равна 54. Найди неизвестные числа (1 балл).
3. В первом бидоне в 3 раза больше молока, чем во втором. Если из первого перелить во второй 20 л, то молока в бидонах будет поровну. Сколько молока в каждом бидоне? (2 балла).
4. Автомобиль ехал 3 часа по шоссе и 2 часа – по проселочной дороге, где его скорость была на 15 км/ч меньше, чем на шоссе. Всего за 5 часов автомобиль проехал 270 км. Найдите скорость автомобиля на шоссе и на проселочной дороге. (2 балла).
2 уровень
1. Определите скорость полета шмеля, если известно, что она в 4 раза и на 15 м/с меньше скорости полета скворца? (1 балл)
2. Можно ли 114 карандашей разложить в три коробки так, чтобы во второй коробке было на 2 карандаша меньше, чем в первой и на 12 карандашей больше, чем в третьей? (1 балл)
3. Десяти собакам и кошкам скормили 56 галет. Каждой собаке досталось 6 галет, а каждой кошке – 5. Сколько было собак и сколько кошек? (2 балла)
4. Разность двух чисел 33. Найдите эти числа, если 0,3 большего из них равны ![]() меньшего. (2 балла)
меньшего. (2 балла)
3 уровень
1. В хозяйстве имеются куры и овцы. Сколько тех и других, если известно, что у них вместе 19 голов и 46 ног? (2 балла)
2.Старинная задача (Греция). Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?
- Вот сколько, - ответил философ, - половина изучает математику, четверть музыку, седьмая часть пребывает в молчании и, кроме этого, есть еще три женщины. (2 балла)
3. В растворе содержится 40% соли. Если добавить 120 г соли, то в растворе будет содержаться 70% соли. Сколько граммов соли было в растворе первоначально? (подсказка: попробуй составить пропорцию) (2 балла)
4. Разведчик доложил командиру, что поезд, за которым он вел наблюдение, прошел мимо него за 15 сек., а мост поезд прошел полностью за 45 сек. Командир знал, что длина моста 450 м и быстро вычислил длину и скорость поезда. Сделай это и ты. (3 балла)
Приложение 1. Оценочный лист учащегося.
Приложение 2. Таблица ответов
Приложение 1.
Оценочный лист учащегося
| Количество баллов | Оценка | |
| Самостоятельная работа | | |
| Задачи для самостоятельного решения | | |
Критерии оценки
| Количество баллов | оценка | |
| Самостоятельная работа | 2-3 балла 4-5 баллов 6 баллов | «3» «4» «5» |
| Задачи для самостоятельного решения | 2-3 балла 4-5 баллов 6-9 баллов | «3» «4» «5» |
Приложение 2. Таблица ответов
Самостоятельная работа
| Вариант 1 | Вариант 2 | Вариант 3 | |
| 1 | -1,3 | -4,2 | -0,6 |
| 2 | 2 | 4 | -14 /17 |
| 3 | 1,5 | 1 1/3 | -1 |
| 4 | -1 | -2 | а=2 |
Задачи самостоятельного решения
| 1 уровень | 2 уровень | 3 уровень | |
| 1 | 7; 35 | 5 м/с; 20 м/с | 15; 4 |
| 2 | 9; 63 | Нет, | 28 |
| 3 | 20; 60 | 6 собак, 4 кошки | 160 г |
| 4 | 60км/ч;45 км/ч | 60; 27 | Длина поезда 225м, V=15 м/с |
Здесь представлен конспект к уроку на тему «Решение задач с помощью уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

