Конспект урока «Треугольники» по математике для 7 класса
Тем, кто учит геометрию,
Тем, кто учит геометрии,
Тем, кто любит геометрию,
Тем, кто еще не знает,
Что может любить геометрию,
Урок геометрии посвящается.
7 класс.
Урок обобщения и применения знаний по теме:
«Треугольники».
Цели:
Обучающие:
-
обобщить и систематизировать материал по данной теме, применять его для практических задач;
-
закрепление знаний формулирований и доказательств признаков равенства треугольников;
-
выработка навыков решения задач с использованием признаков равенства треугольников;
-
научить обобщать знания, осмысливать материал, делать выводы по материалу обязательного уровня;
-
развитие аккуратности при геометрических построениях.
Развивающие:
-
провести диагностику усвоения системы знаний и умений, и ее применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень;
-
развитие познавательного процесса, памяти, воображения, мышления, внимания, наблюдательности, сообразительности.
Воспитательные:
-
показать межпредметную связь математики с другими дисциплинами;
-
содействовать рациональной организации труда;
-
введением игровой ситуации создать положительную эмоциональную обстановку;
-
выработать самооценку в выборе пути; критерии оценки своей работы и работы товарища;
-
повысить интерес учащихся к нестандартным задачам.
-
формирование у учащихся положительной мотивации к обучению.
Содержание темы:
Данная тема программы 7-го класса по геометрии действующего учебника Л.С.Атанасян, В.Ф.Бутузов и др., Геометрия, 7-9 класс, М.: Просвещение, 2003 г.из Федерального комплекта.
Тип урока:
Урок обобщения, систематизации и применения знаний.
Организационные формы общения:
Коллективная, групповая, парная, индивидуальная.
Учебно-методическое обеспечение:
ПК, плакаты: признаки равенства треугольников, равнобедренный треугольник, учебник геометрии, доска, индивидуальные карточки, эстафетные карточки, карточки обратной связи, циркули, линейки, треугольники, ножницы, цветная бумага.
Структура урока
-
Мотивационная беседа с последующей постановкой цели урока.
-
Актуализация опорных знаний.
-
Закрепление знаний. Решение задач. Игровые действия, включающие познавательное содержание и диагностирующий уровень усвоения системы знаний и умений каждого учащегося по заданной теме на этом этапе обучения.
-
Подведение итогов урока.
-
Домашнее задание.
-
Рефлексия.
Ход урока.
-
Мотивационная беседа с последующей постановкой цели урока.
Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательства большей части теорем курса строятся по схеме:
поиск равных треугольников.
![]()
доказательство их равенства
![]()
следствия, вытекающие из равенства треугольников.
Признаки равенства треугольников открывают широкие возможности для решения задач, и таким образом, позволяют накапливать опыт доказательных рассуждений.
-
Актуализация опорных знаний.
Фронтальный опрос.
Верно ли утверждение (карточки обратной связи: верно – зеленая карточка; неверно – красная карточка):
-
Высота равнобедренного треугольника, проведенная к основанию, является его медианой и биссектрисой.
-
Два треугольника равны, если 3 угла одного треугольника соответственно равны трем углам другого треугольника.
-
В равнобедренном треугольнике биссектриса, проведенная к основанию, делит его на два равных треугольника.
-
Высота любого треугольника проходит внутри треугольника.
-
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны.
-
Три точки и три отрезка, соединяющие эти точки попарно, определяют геометрическую фигуру, которая называется многоугольником.
-
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
-
В равнобедренном треугольнике основание и биссектриса , проведенная к основанию, взаимно перпендикулярны.
-
Если в треугольнике высота, проведенная к основанию, является биссектрисой, то этот треугольник равнобедренный.
Доказать первый признак равенства треугольников по готовому чертежу.
Доказать теорему о биссектрисе равнобедренного треугольника, проведенной к основанию.
Карточки для устного опроса (4 человка)
(на компьютере)
7 класс, «Треугольники».
Карточка для устного опроса.
Вариант 1.
-
Сформулируйте первый признак равенства треугольников.
-
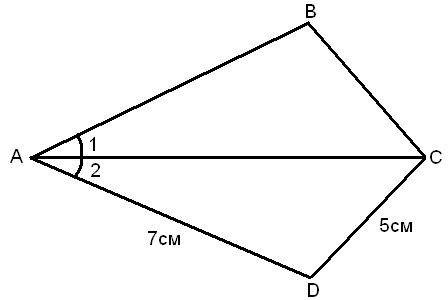
На рисунке АВ = DB,
 1 =
1 =  2. Докажите, что ∆АВС = =∆DВС.
2. Докажите, что ∆АВС = =∆DВС.
7 класс, «Треугольники».
Карточка для устного опроса.
Вариант 2.
-
Сформулируйте второй признак равенства треугольников.
-
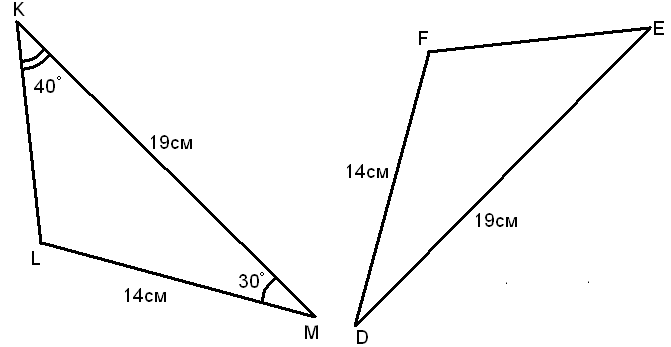
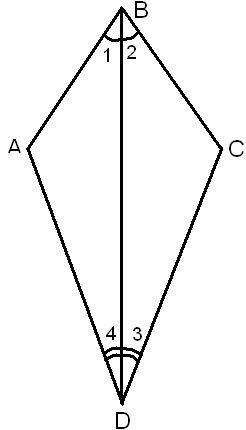
На рисунке
 1 =
1 =  2,
2,  3 =
3 =  4. Докажите, что ∆АВD = ∆CBD.
4. Докажите, что ∆АВD = ∆CBD.
7 класс, «Треугольники».
Карточка для устного опроса.
Вариант 3.
-
Сформулируйте третий признак равенства треугольников.
-
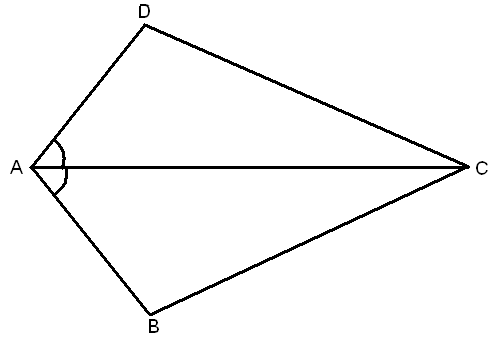
На рисунке АВ = DC, ВС = AD. Докажите, что ∆АВС = ∆CDА.

7 класс, «Треугольники».
Карточка для устного опроса.
Вариант 4.
-
Сформулируйте свойство углов равнобедренного треугольника.
-
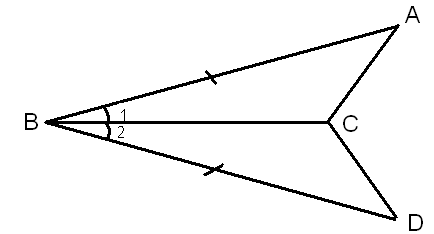
На рисунке АВ = ВС, AD = DC. Докажите, что
 ВАD =
ВАD =  BCD.
BCD.

Практическая работа.
Выполняется с помощью цветной бумаги и ножниц.
| Практическая работа.
| |
| Практическая работа.
2. Вырезать из бумаги остроугольный треугольник. С помощью необходимых перегибаний убедиться, что высоты треугольника пересекаются в одной точке. | Практическая работа. Господин Новоселов из Перловки спрашивает: «Как разрезать треугольную плиту для садовой дорожки на 3 части так, чтобы из нее можно было сложить прямоугольник. |
.
-
Закрепление знаний. Решение задач. Игровые действия, включающие познавательное содержание и диагностирующий уровень усвоения системы знаний и умений каждого учащегося по заданной теме на этом этапе обучения.
Эстафета.
-
Сколько треугольников на рисунке.
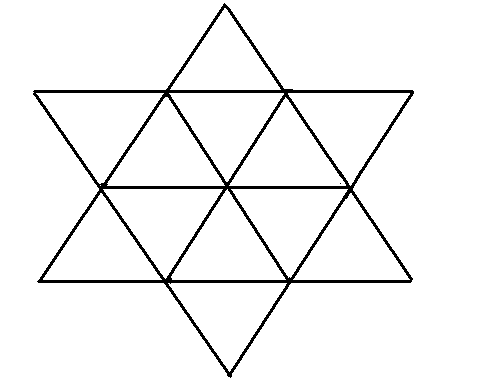
-
Назовите автора учебника по геометрии, по которому вы учитесь.
-
Сколько треугольников на рисунке?
![]()
-
Вычислите периметр треугольника.
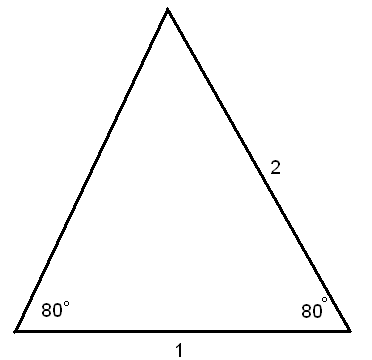
4. Можно ли какой-нибудь разносторонний треугольник разрезать на два равных треугольника?
5. Сколько биссектрис имеет треугольник?
6. Единица измерения плоских углов.
Игра «Угадай героя-треугольника».
Учащиеся делятся на две команды. Затем учитель показывает первой команде сложенный листок, на котором нарисован один из видов треугольника, и предлагает второй команде угадать этот треугольник. Для этого вторая команда может задавать первой команде непрямые вопросы по поводу этого треугольника. Затем берется другой чертеж и команды выполняют тот же процесс, но наоборот. Побеждает та команда, которая справилась с заданием с помощью меньшего количества вопросов.
Игра «Аукцион».
В игре участвуют 4 команды. С помощью кодоскопа на экран проецируется лот №1 – пять заданий на доказательство равенства треугольников. Первая команда выбирает задание и назначает ему цену от 1 до 5 баллов. Если цена этой команды выше тех, что дают другие, она получает это задание и выполняет его, остальные задания должны купить другие команды. Если задание решено верно, команде начисляются баллы – цена этого задания, если неверно, то эти баллы (или часть их) снимаются.
Готовые чертежи.
1. По данным на чертеже найти DH.
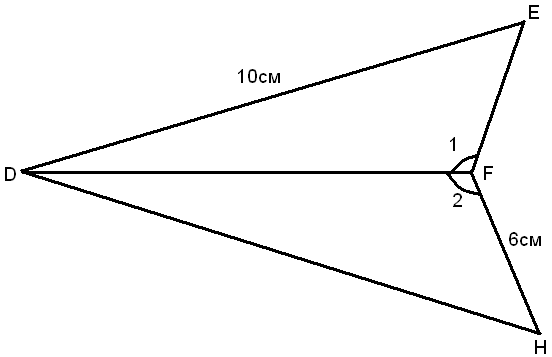
-
Найти пары равных треугольников и доказать их равенство.

-
Найти пары равных треугольников и доказать их равенство.
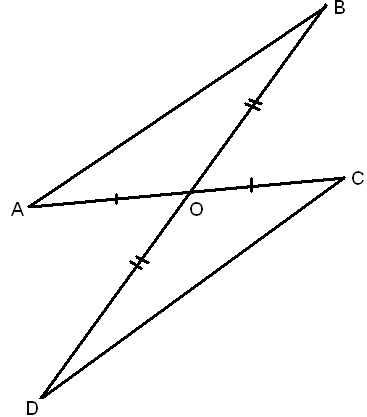
-
Найти пары равных треугольников и доказать их равенство.
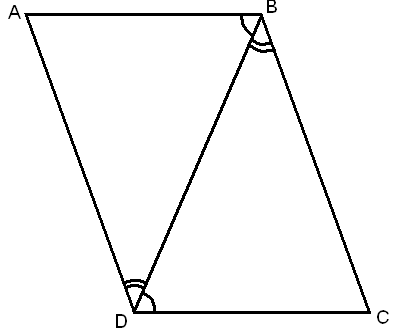
-
По данным чертежа найти длину отрезка КМ.
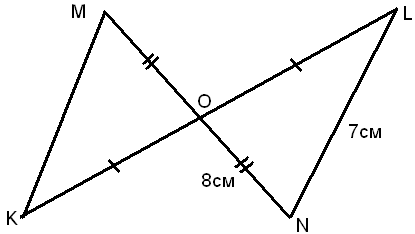
Решение задач.
Задача 1.
В равнобедренном треугольнике основание относится к боковой стороне как 3 : 4. Найдите стороны треугольника, если периметр его равен 33см.
Дано:
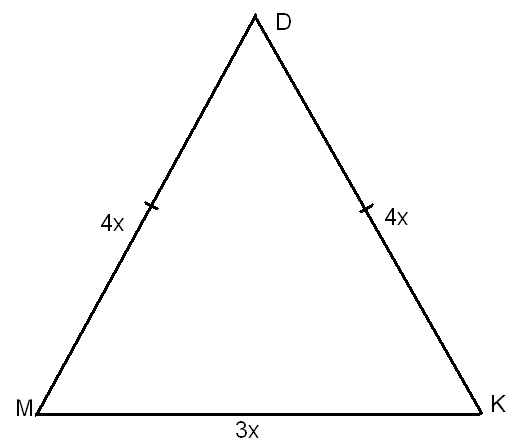 ∆MDK; MD = DK, MK : MD = 3 : 4, Р = 33 см.
∆MDK; MD = DK, MK : MD = 3 : 4, Р = 33 см.
Найти: МК, MD, DK.
Решение.
Пусть на одну часть приходится х см, тогда МК = 3х см, MD = DK = 4х см.
По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3.
МК = 9 см, MD = DK = 12 см.
Ответ: 9 см; 12 см; 12 см.
№164 (по учебнику).
На сторонах равностороннего треугольника АВС отложены равные отрезки AD, BE, CF, как показано на рисунке. Точки D, E, F соединены отрезками. Докажите, что треугольник DEF – равносторонний.
Дано:
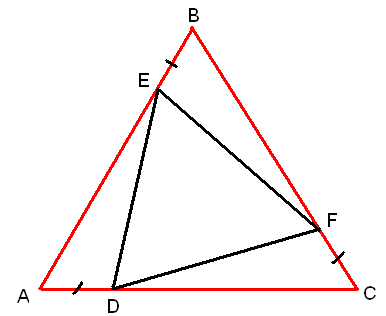 ∆АВС, АВ = ВС = АС, АD = CF = BE.
∆АВС, АВ = ВС = АС, АD = CF = BE.
Доказать ∆DEF – равносторонний.
Доказательство.
Чтобы доказать, что ∆DEF – равносторонний, нужно доказать, что DE = EF = DF.
Рассмотрим ∆BEF, ∆CDF, ∆ADE.
В этих треугольниках
![]()

 А =
А =![]() В =
В =![]() С,
С,
АD = CF = BE, ∆BEF = ∆CDF = ∆ADE по двум сторонам и углу между AE = BF = CD. ними.
Значит, в этих треугольниках ED = DF = FE, следовательно, ∆DEF – равносторонний, что и требовалось доказать.
Задача №150.
Даны окружность, точка А, не лежащая на ней, и отрезок РQ. Постройте точку М на окружности так, чтобы АМ = PQ. Всегда ли задача имеет решение?
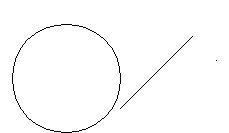
-
Подведение итогов урока. Тест. (взаимопроверка)
Ф.И. _________________________________
Заполните таблицу
| 1 | 2 | 3 | 4 | 5 | 6 | |
| № ответа | | | | | | |
7 класс, геометрия.
Признаки равенства треугольников.
| Найти стороны треугольника, периметр которого равен 27 см, если одна из них на 5 см больше второй и на 1 см больше третьей стороны. 1) 7 см, 8 см, 12 см; 2)6 см, 10 см, 11 см; 3) | |
| 2 | В треугольниках АВС и ADC на чертеже 1) 5 см; 2) 7 см; 3) данных недостаточно. |
| 3 | Боковая сторона равнобедренного треугольника равна 19 см, а его периметр – 48 см. Найти длину основания треугольника. 1) 10 см; 2) 14,5 см; 3) 29 см. |
| 4 | К данным на чертеже элементам треугольника DEF задать еще один элемент так, чтобы ∆DEF = ∆KLM.
1) |
| 5 | Отметить на чертеже недостающие равные элементы данных треугольников так, чтобы треугольники ADC и АВС были равны по стороне и двум прилежащим углам. 1) AD = AB; 2) |
| 6* | Окружности с радиусами 30 см и 40 см касаются. Найти расстояние между их центрами. 1) 10 см; 2) 70 см; 3) 10 см или 70 см; |
5. Домашнее задание.
Обращается внимание на записанное на доске домашнее задание.
Вопросы для повторения 1 -21; задачи №170, 171, 185.
6.Рефлексия.
Проводится беседа о форме урока; о том, что нового узнали; о том, что необходимо изменить, чтобы было интереснее.
Здесь представлен конспект к уроку на тему «Треугольники», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.