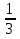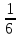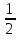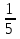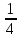Конспект урока «ГРАФЫ» по математике для 6 класса

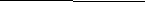ГРАФЫ

математика 6 класс

Цели урока:

Образовательные:

организовать деятельность обучающихся по осознанию и осмыслению понятия «графы», «уникурсальные графы»

Развивающие:

создать условия для развития интеллектуальных умений: умения формулировать проблему, выдвигать гипотезу, умения анализировать, сравнивать, обобщать делать выводы.

Воспитательные:

способствовать воспитанию чувства удовлетворения и успеха от интеллектуального труда.

Тип урока: изучение нового материала.

Используемое оборудование: мультимедийный проектор; компьютер.

План урока:

1. Организационный момент

2. Объяснение нового материала

1. Сообщение темы урока

2. Историческая справка

3. Зарождение теории графов (задача Эйлера о мостах Кенигсберга)

4. Объяснение нового материала

1. Введение новых понятий

2. Отработка навыков. Практическая работа

3. Уникурсальный граф

Работа в группах

1. Решение задачи Эйлера

3. Физкультминутка

4. Закрепление пройденного материала.

   1. Решение задач

   2. Связь с жизнью

5. Подведение итогов урока.

Рефлексия

ГРАФЫ

(математика 6 класс)

Цели урока:

Образовательные:

организовать деятельность обучающихся по осознанию и осмыслению понятия «графы», «уникурсальный граф»

Развивающие:

создать условия для развития интеллектуальных умений: умения формулировать проблему, выдвигать гипотезу, умения анализировать, сравнивать, обобщать делать выводы.

Воспитательные:

способствовать воспитанию чувства удовлетворения и успеха от интеллектуального труда.

Тип урока: изучение нового материала.

Используемое оборудование: мультимедийный проектор; компьютер.

План урока:

6. Организационный момент

7. Объяснение нового материала

5. Сообщение темы урока

6. Историческая справка

7. Зарождение теории графов (задача Эйлера о мостах Кенигсберга)

8. Объяснение нового материала

5. Введение новых понятий

6. Отработка навыков. Практическая работа

7. Уникурсальный граф

Работа в группах

1. Решение задачи Эйлера

8. Физкультминутка

9. Закрепление пройденного материала.

   1. Решение задач

   2. Связь с жизнью

10. Подведение итогов урока.

Рефлексия

1. Организационный момент

(Слайд 1) Музыка.

- Здравствуйте ребята!

Я – учитель средней общеобразовательной школы села Мизино-Лапшиновка, Загертдинова Наталья Павловна. Сегодня я приехала к вам, чтобы провести урок математики.

Сегодня вы принимаете гостей, а это своего рода праздник! И настроение должно быть соответствующее.

Я надеюсь, что музыка способствует вашему положительному эмоциональному настрою на урок.

Перед вами на столе лежат «мордашки». Нужно показать ту, которая соответствует вашему настроению в данный момент.

«МАТЕМАТИКА» - это стройное, красивое здание, по этажам которого вы шагаете с 1-го класса.

Сегодня вы пройдете очередной шаг по дороге знаний, и я с радостью помогу вам сделать этот шаг.

Однажды я прочла следующее высказывание:

С тех пор, как существует мирозданье,

Такого нет, чтоб не нуждался в знанье.

Какой мы не возьмем язык и век,

Всегда стремился к знанью человек.

Б.Паскаль

1. Что в вашем понимании означает «стремиться к знанью»? (анализировать, делать выводы, сравнивать, размышлять).

2. И к какому же результату в итоге приходит человек?

3. К чему приводит мощь человеческого разума? (делать открытия, выдвигать новые идеи).

Вот и сегодня на уроке вы будете думать, размышлять, анализировать, делать выводы!!!

Пусть эти слова будут эпиграфом к нашему уроку.

Приготовьте тетрадь к работе (число, .кКл. работа.тТема - позже).

2. Объяснение нового материала

1. Сообщение темы урока

Но я думаю, что прежде всего вам бы хотелось узнать тему сегодняшнего урока.

А для этого вы должны выполнить следующее:

Перед вами на столах лежат карточки, в которых закодирована тема нашего урока.

Вы наверное обратили внимание, что математика в 6 классе «построена на дробях»

1. А что такое дробь?

2. Какая дробь называется правильной?

3. Какая дробь называется неправильной?

(Перед учащимися на столах лежат карточки с закодированными в них словами)

Вариант I

Расположите дроби в порядке убывания

Й	Р	Э	Е	Л

(ЭЙЛЕР)

Вариант II

Расположите дроби в порядке возрастания

Ф	Г	Ы	Р	А

(ГРАФЫ)

Расположив дроби в определенном порядке, вы получите закодированные слова, определяющие тему нашего сегодняшнего урока.

Итак, I вариант … (Эйлер)

II вариант … (Графы)

(Слайд 2)

Тема нашего урока «Графы»

2. Историческая справка

Я вам сегодня немного расскажу про знаменитого математика Леонарда Эйлера, который родился в 18 веке в Швейцарии, но большую часть своей жизни, он прожил у нас в России, в Санкт-Петербурге. Еще при жизни он был признан первым математиком мира.

Леонард Эйлер первым заложил теорию графов, которая позволяет нам с вами решать различные задачи: в частности олимпиадные, так называемые задачи со звездочкой, задачи математического конкурса Кенгуру.

А началось изучение теории графов со знаменитой задачи Эйлера о мостах Кенигсберга.

3. Зарождение теории графов (задача Эйлера о мотах Кенигсберга)

(Слайд 3)

Леонард Эйлер гулял в городе Кенигсберге по берегу реки Приголь. Жители города задали ему вопрос: Можно ли совершить прогулку по семи мостам через реку Приголь так, чтобы каждый мост не проходить дважды?

Что сделал Леонард Эйлер?

Он изобразил острова в виде точек, мосты – в виде линий и получил первый «граф» (схему)

К этой задаче мы вернемся позже, а сейчас познакомимся, что такое «граф».

4. Объяснение нового материала

   1. Введение новых понятий

Граф – это набор точек, каждые из которых соединены линиями.

Точки – называются вершинами, а соединяющие их линии (я не сказала отрезки) – ребрами.

(Слайд 4)

Давайте посчитаем сколько в этом графе

вершин (3)

ребер (3)

Посмотрите еще на один граф. Посчитайте:

количество ребер (7)

вершин (5)

Число ребер, выходящих из каждой вершины графа мы будем называть степенью этой вершины.

Если из вершины выходит нечетное число ребер – она будет называться нечетной, а если четное – четной.

1. Назовите, пожалуйста, сколько ребер выходит из каждой вершины и назовите степень вершины каждого графа (дети отвечают на поставленный вопрос)

2. Скажите: сколько ребер, сколько вершин, какова сумма степеней? (дети отвечают)

3. А как вы думаете: как связаны количество ребер и сумма степеней? (количество ребер *2= сумма степеней)

2. Отработка навыков. Практическая работа

А теперь выполним практическую работу. Переверните лист. Перед вами небольшая памятка.

Попробуем построить граф под номером 1.

Прежде, чем приступить к выполнению работы, ответьте на следующие вопросы:

1. Что такое граф?

2. Вершины?

3. Ребра?

4. Как определить степень вершины?

5. Когда вершина называется четной, а когда нечетной?

6. Как связано количество ребер и сумма степеней?

А теперь посмотрим на первое задание.

1. Сколько вершин в этом графе?

2. Посчитайте сумму степеней

3. Чтобы узнать количество ребер, что нужно сделать? (Найти сумму степеней и разделить на 2)

Таким образом, постройте 4 вершины и попробуйте построить граф. (дети выполняют работу)

(В дальнейшем для проверки вызываются два ученика, которые демонстрируют свои схемы – проверяется количество вершин, ребер, степени вершин)

А теперь выполним построение второго графа, но перед построением ответим на вопросы:

1. Сколько вершин?

2. А сколько ребер?

3. Какой вывод сделаем? (У нас не получится построить граф, т.к. количество ребер – дробное)

Верно, молодцы!

3. Уникурсальный граф

А теперь я попрошу вас вспомнить – рисовали ли вы «домик» не отрывая карандаша от бумаги?

(Конечно)

Оказывается, вы не просто рисовали – вы строили уникурсальный граф.

Работа в группах

(Слайд 5)

Я вас прошу взять листок с таким же рисунком, что и у меня на доске. Необходимо выяснить какую фигуру можно построить не отрывая карандаша от листа бумаги, а какую – нельзя. (Дети выполняют задание)

Какая группа готова?

(Вызывается ученик к доске, который отвечает на поставленный вопрос. Идет обсуждение с классом о правильности выполнения задания, рисуется «домик»)

1. Давайте посчитаем степени вершин каждого графа.

2. Почему мы не смогли один из графов построить, не отрывая карандаша от бумаги? (у него все вершины имеют нечетную степень)

4. Решение задачи Эйлера

(Слайд 6)

Вернемся к нашей задаче.

1. Можно ли совершить прогулку по мостам города Кенигсберга, не разу на пройдя по одному и тому же мосту дважды?

2. Является ли этот граф уникурсальной фигурой?

3. Можно ли его нарисовать не отрывая карандаша от бумаги и не проводя каждую линию дважды?

4. Что мы должны для этого посчитать? (степени вершин – нечетные)

Вывод: нет, нельзя, все вершины имеют нечетную степень.

3. Физкультминутка

Бежит стремглав минутка.

Минутка коротка,

Но за минутку можно

Найти звезду, жука,

Решение задачи

И редкий минерал,

Который до сих пор еще

Никто не открывал.

4. Закрепление материала.

   1. Решение задач

А мы с вами рассмотрим задачу, которую нам поможет решить знание теории графов.

(вызывается ученик к доске)

(Слайд 7)

Задача 1

Перед вами 5 утверждений. Надо определить, какое утверждение истинно,

какое ложно.

Свою работу мы начнем с построения схемы

(ученик строит схему)

Вопросы:

1. Как называется схема, которую мы с вами построили (граф)

(Слайд 8)

Задача 2

Посмотрим следующую задачу.

Алеша, Боря и Витя учатся в одном классе. До дома дети ездят на автобусе, трамвае и троллейбусе. Однажды после уроков Алеша пошел провожать друга до автобусной остановки. Когда мимо них проходил троллейбус, кто-то неожиданно выкрикнул из окна троллейбуса – «Боря, ты оставил портфель в школе». На каком транспорте каждый из мальчиков добирается до дома? (Алеша – трамвай, Боря – автобус, Витя – троллейбус)

2. Связь с повседневной жизнью

(Слайд 9,10,11)

А теперь, давайте с вами попробуем ответить на вопрос, а где в повседневной жизни мы с вами встречаем графы?

(карты-схемы: любая карта дорог, метро, карта поселка с улицами и т.п.)

Правильно. Это карты-схемы. Посмотрите. Перед вами карта-схема вашего

поселка и Татищевского района, а также схема метро города Санкт-Петербург.

(Слайд 12)

И если вы будете в Питере, вы пользуясь схемой метро, никогда там не заблудитесь, и может быть кто-то из вас вспомнит о знаменитом ученом – математике, гениальнейшем человеке – Леонарде Эйлере, чье творчество стало достоянием всего человечества.

До сих пор школьники всего мира изучают тригонометрию, логарифмы в том виде, который придал им Леонард Эйлер

5. Подведение итогов

Я думаю, что вам было интересно, и вернувшись к нашему эпиграфу урока

(Слайд 13)

С тех пор, как существует мирозданье,

Такого нет, чтоб не нуждался в знанье.

Какой мы не возьмем язык и век,

Всегда стремился к знанью человек.

Б.Паскаль

Позвольте высказать свое мнение: знания, полученные сегодня на уроке может быть пригодятся вам в жизни.

Рефлексия

(Слайд 15)

Чтобы вы могли глубже оценить свою деятельность и вклад в урок предлагаю закончить следующие фразы…

1. Сегодня на уроке я узнал…

2. Сегодня на уроке мне понравилось…

3. Сейчас мое настроение ….

Спасибо за урок.

Музыка

И уходя из класса я прошу вас оценить урок, прикрепив к доске «сердечко» - если урок вам понравился и вам все было понятно, «молнию» - если у вас остались какие-то вопросы и «круг» - если вам ничего не понравилось на уроке.

Вариант I

Расположите дроби в порядке убывания

Й	Р	Э	Е	Л

Вариант II

Расположите дроби в порядке возрастания

Ф	Г	Ы	Р	А

1. Граф – это набор точек, каждые из которых соединены линиями.

2. Точки – называются вершинами, а соединяющие их линии (я не сказала отрезки) – ребрами.

3. Число ребер, выходящих из каждой вершины графа мы будем называть степенью этой вершины.

4. Если из вершины выходит нечетное число ребер – она будет называться нечетной, а если четное – четной.

5. Как связаны количество ребер и сумма степеней? Количество ребер*2= сумма степеней вершин

Практическая работа

1. Постройте граф, если

А – 3

B – 3

C – 2

D – 2

2. Постройте граф, если

А – 2

B – 3

C – 1

D – 2

Е – 3