Конспект урока «Решение задач тригонометрических уравнений» по математике для 10 класса

Алпысбаева Айнагул Тюрехановна

Учительница по математики

им. Г.Муратбаева № 17 школ

Класс: 10 б

Тема: «Решение задач тригонометрических уравнений»

Цель: систематизация знаний по изучаемой теме, отработка навыков решения уравнений, контроль знаний учащихся.

ХОД УРОКА

I. Оргмомент

II. Устные упражнения

1. Решение уравнений: ; ;

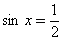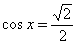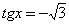
2. Имеет ли смысл выражение: ; ; ;

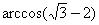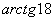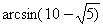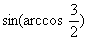
3. Вычислить:

III. Проверка домашнего задания с объяснением решения учащимися

Домашнее задание: несколько учеников записывают на доске во время перемены.

1.

2. =
   

3.
   нет решений

4.

5.

6.

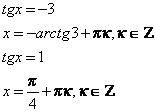
Домашнее задание проверяется по готовым ответам, и выставляются оценки:

«3» – 4 правильно решенных уравнения
«4» – 5 правильно решенных уравнения
«5» – 6 правильно решенных уравнения

IV. Математический диктант

Условие записано на доске

Решите уравнения.

I.1.

2.

3.

4.

5.

6.

Ответы записаны на обратной стороне доски.

Сразу проверяем и выставляем оценки.

V. Систематизация знаний по теме

а) Историческая справка о возникновении тригонометрии (в виде сообщения одного из учеников)

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon – треугольник, а metrew – измеряю).

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухаммед-бен Мухаммед (940-998), который составил таблицы синусов и тангенсов через 10 с точностью до 1/604.
Теорему синусов уже знали индийский ученый Бхаскара и азербайджанский астроном и математик Насиреддин Туси Мухаммед (1201-1274).
Кроме того, Насиреддин Туси в своей работе «Трактат о полном черырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Длительную историю имеет понятие синус. Фактически различные отношения отрезког треугольника и окружности (а, по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского.
В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия.
Современный синус, например, изучался как полухорда, на которую опирается центральный угол величиной а, или как хорда удвоенной дуги.

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского ученого Ариабхаты. Отрезок он назвал ардхаджива.
Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость).
При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т.е. «дополнительный синус».

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов.

Эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы: благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной в Европе. Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1607) и Иоганна Кеплера (1571-1630), а также в работу математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т.д. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук.

Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказывать путем формального применения формул тригонометрии, доказательства стали намного компактнее и проще.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

б) Классифицируем тригонометрические уравнения:

Рассматриваем типы тригонометрических уравнений и из набора уравнений выбираем уравнения каждого типа.

1. Простейшие тригонометрические уравнения.
2. Решения уравнений с помощью замены переменной.
3. Решение уравнений разложением на множители.
4. Решение однородных уравнений I степени.
5. Решения однородных уравнений II степени.

1. 9.

2. 10.

3. 11.

4. 12.

5. 13.

6. 14.

7. 15.

8.

в) Выполняем решение примеров уравнений по группам:

• I группа 8, 9, 5, 3, 1;

• II группа 10, 13, 2, 7, 11;

• III группа 12, 4, 6, 14, 15.

Решившие первыми учащиеся получают оценки и помогают остальным учащимся.

VI. Тест

I  уровень

1. Какое из данных уравнений не имеет корней:

1)
2)
3)
4)

Ответы:

1) 1 и 2
2) 1 и 4
3) 2 и 4
4) другой ответ

2. Какое из данных выражений не имеет смысла:

1)
2)
3)
4)

Ответы:

1) 1
2) 1 и 3
3) 4
4) 3

3. Вычислить:

Ответы:

1)
2) 0
3)
4)

4. Решить уравнение:

Ответы:

1)
2)
3)
4)

5. Решить уравнение:

Ответы:

1)
2)
3)
4)

6. Решить уравнение:

Ответы:

1)
2)
3)
4)

II уровень

1. Какое из данных уравнений не имеет корней:

1)
2)
3)
4)

Ответы:

1) 1 и 2
2) 1 и 4
3) 1, 2 и 4
4) другой ответ

2. Какое из данных выражений не имеет смысла:

1)
2)
3)
4)

Ответы:

1) 1 и 2
2) 3
3) 4
4) 3 и 4

3. Вычислить:

Ответы:

1) 10
2) 10,8
3) 0,8
4) 10,6

4. Решить уравнение:

Ответы:

1)
2)
3)
4)

5. Решить уравнение:

Ответы:

1)
2)
3)
4)

6. Решить уравнение:

Ответы:

1)
2)
3)
4) нет решений

VII. Домашнее задание: придумать по одному уравнению каждого типа и решить их.

VIII. Подведение итогов урока