Конспект урока «Неизвестная известная парабола» по алгебре

МБОУ «СОШ №7»

Урок – панорама «Неизвестная известная парабола»

(Заключительный урок по теме:

«Квадратичная функция, её свойства и график»

с использованием активных методов)

Белоусова Елена Николаевна,

учитель математики

Нальчик,

2011 - 12 учебный год

Урок – панорама «Неизвестная известная парабола»

Урок заключительный по теме: «Квадратичная функция, её свойства и график» с использованием активных методов (слайды 1-5).

Цели урока:

1. Повторить свойства квадратичной функции.

2. Закрепить их знание при построении графиков квадратичной функции.

3. Уметь определять свойства функции по графику.

4. Показать связь квадратичной функции и её графика с реальным миром

Учебно-воспитательные задачи:

Образовательные:

• Приобретение знаний по применению графического изображения квадратичной функции.

• Применение приемов решения задач.

Развивающие:

• Совершенствование умения строить параболу.

• Применение свойств квадратичной функции в других и их взаимосвязь с математикой.

Воспитательные:

• Пробудить интерес к истории математики.

• Способствовать расширению кругозора через информационный материал, диалоги и совместные размышления.

Оборудование:

Ход урока

1. Организационный момент.

2. Вести с урока.

1. повторить определение квадратичной функции, ее свойства и график. (Фронтальная работа).

2. понятие параболы. (Ученик объясняет, используя компьютерную презентацию)

3. различие параболы: по направлению ветвей, по координатам вершин, по коэффициенту

4. Применение параболы в физике, технике, архитектуре, в природе, в повседневной жизни.(представление проектов учащихся)

1.Определение (слайд 6)

Функция вида у = ах²+bх+с,

где а, b, c – заданные числа, а≠0,

х – действительная переменная, называется квадратичной функцией.

Примеры:

1) у=5х+1 4) у=x³+7x-1

2) у=3х²-1 5) у=4х²

3) у=-2х²+х+3 6) у=-3х²+2х

График квадратичной функции -Парабола (слайд 7)

Свойства квадратичной функции (слайд 8)

• Парабола — кривая второго порядка.

• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.

• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

• Парабола является антиподерой прямой.

• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

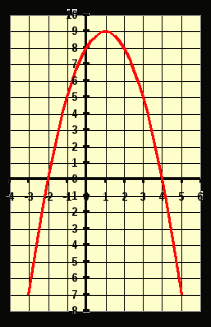Задание (Слайд 9)

• Определить координаты вершины параболы.

• Уравнение оси симметрии параболы.

• Нули функции.

• Промежутки, в которых функция возрастает, убывает.

• Промежутки, в которых функция принимает положительные значения, отрицательные значения.

• Каков знак коэффициента a ?

• Как зависит положение ветвей параболы от коэффициента a ?

Слайд 10

Вершина параболы:

Уравнение оси симметрии: х=х₀

Задание.

Найти координаты вершины параболы:

1) у = х 2 -4х-5 2) у=-5х 2+3

Ответ:(2;-9) Ответ:(0;3)

Слайд 11.

Координаты точек пересечения параболы с осями координат.

• С Ох: у=0 ах2+bх+с=0

• С Оу: х=0 у=с

Задание.

Найти координаты точек пересечения параболы с осями координат:

1)у=х²-х; 2)у=х²+3; 3)у=5х²-3х-2

Ответ:(0;0);(1;0) (0;3) (1;0);(-0,4;0);(0;2)

Тест. Слайд 12

Слайд 13

Построить график функции и по графику выяснить ее свойства.

у = -х²-6х-8

По графику определите свойства функции:

у>0 на промежутке… (-4;-2)

у (-∞;-4);(-2;∞)

функция возрастает на промежутке… (-∞;-3]

функция убывает на промежутке… [-3;∞)

наибольшее значение функции равно… 1, при х=-3

Тест. Слайд 14

Защита проектов учащихся

1. 1.Построение параболы

2. Связь с космическим миром

3. Применение параболы в физике, технике, баллистике.

4. Траектория движения

5. Парабола в архитектуре и строительстве- парабола

6. Парабола вокруг нас

7. Из истории математики: Диалог Герона и Архимеда о применениях параболических зеркал.

Итог урока

• Рефлексия:

• испытывали ли вы затруднение при работе с тестами?

• была ли интересна для вас информация, которую вы получили?

• где вы можете применять полученные знания?

• где вообще применяются графическое изображение и свойства квадратичной функции?

Домашнее задание:учебник «Алгебра 9», Стр. 44-45

• № 121(а)

• №123

• №128

Литература

• Бураго Д. Ю., Бураго Ю. Д., Иванов С. В. Курс метрической геометрии НИЦ РХД, Институт компьютерных исследований, Инст-т компьют. исслед., Ин-т комп.исслед., ИКИ, , ISBN 5-93972-300-4, 2004

• Математический энциклопедический словарь. М. «Советская энциклопедия», 1988 г

• Бронштейн И., Парабола, Квант, № 4, 1975.

• Математическая энциклопедия (в 5-и томах), Москва, «Советская Энциклопедия», 1982 г.

• Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Гостехиздат 1952 г., 32 стр.

• А. А. Акопян, А. В. Заславский Геометрические свойства кривых второго порядка. Москва, Издательство МЦНМО, 2007 год.

• Интернет ресурсы

Из истории математики:

Диалог Герона и Архимеда о применениях параболических зеркал.

Диалог в ролях:

Архимед: Государь! Какая неожиданность в столь поздний час! Чем я обязан чести визита царя Гиерона в мой скромный дом?

Гиерон: Архимед дорогой друг сегодня вечером в моем дворце был пир в честь великой победы нашего маленького города Сиракузы над могущественным Римом. Я приглашал тебя, но твое место осталось пустым. Почему же ты не пришел - ты кому главным образом мы обязаны сегодняшней победой? Твои громадные вогнутые медные зеркала подожгли десять из двадцати больших кораблей римлян. Подобные огненным факелам они покинули гавань гонимые юго-западным ветром, и все затонули, прежде чем достигли открытого моря. Я не смог заснуть, не поблагодарив тебя за избавление нашего города от врага.

Архимед: Ты заставляешь меня краснеть от смущения. Но разреши снова напомнить тебе, что война еще не закончена. Хочешь ли ты услышать мой совет?

Гиерон: Я как царь даже приказываю тебе откровенно высказать своё мнение?

Архимед: Настал момент, когда тебе нужно заключить мир с Римом. Когда же известие о сегодняшней битве достигнет Рима, римляне так рассвирепеют, что не удовлетворятся ничем, кроме полной победы.

Гиерон: Твой анализ верен. Действительно сегодня вечером я получил послание от Марцелла в котором он предлагает мир и отход его войск на определенных условиях. Я принял все его условия кроме одного – отдать тебя в качестве заложника. Я согласился отдать ему сына и дочь, но при условии, что мне двух своих детей. Что касается тебя я сказал ему, что преклонные года не позволяют тебе жить в лагере. Однако, зная, что в действительности, что ему нужен не ты сам, а твоя мудрость я обещал, что подробно опишешь все свои изобретения имеющие военное значение.

Архимед: Я ничего не буду писать о моих изобретениях относительно способов ведения войны. Это был не тот вид деятельности, которым я хотел бы доказать практическую ценность математических идей. Я увидел людей, убитых моими машинами, и почувствовал себя виновным. Я дал торжественную клятву Афине, что никому никогда не открою секрет моих военных машин ни устно, ни письменно. Я пытался успокоить совесть, говоря себе, что новость о победе Архимеда над римлянами с помощью математики достигнет всех уголков мира, говорящего на греческом языке, это будут помнить даже тогда, когда война закончится, и секреты моих военных машин будут похоронены вместе со мной.

Вероятно, я был просто глупцом, но я полагал, что мог бы изменить ход истории. Я был обеспокоен будущим Греции и думал, что, если бы мы приняли математику в больших масштабах – в конце концов, математика является изобретением греков и лучшим достижением греческого ума, - мы могли бы спасти наш греческий образ жизни. Теперь, я считаю, уже поздно. Римляне завоюют не только Сиракузы , но и все остальные греческие города, наше время кончается.

Гиерон: Это правда, мой друг Архимед я получаю вести от властителей, с которыми я поддерживаю дружеские отношения – они интересуются твоими изобретениями.

Ты хочешь сказать, что твои изумительные машины основаны на математике, которую знает каждый образованный человек?

Архимед: Ты недалёк от истины.

Гиерон: Можешь ли ты привести пример?

Архимед: Хорошо, пример приведёт мой ученик.

Ученик Архимеда:

Слова ученика Архимеда: Возьмём в качестве примера зеркало, которое сегодня сослужило такую превосходную службу. Мы просто использовали хорошо известное свойство параболы: если какую-нибудь точку Р параболы соединить с фокусом параболы, а затем провести через Р прямую, параллельную оси, то эти две линии образуют равные углы с касательной к параболе в точке Р. Эту теорему можно найти в труда ученых из Александрии.

Гиерон: Даже не вникая в твои секреты, я понял, что кроме свойств параболы ты должен многое знать о металлах и об искусстве их обработки. Выходит, что значений математики не достаточно, если кто-то хочет применять их на деле. Я думаю, мы должны учится у римлян, тогда нам легче будет воевать с ними.

Я должен идти. Я хочу немного поспать. Завтра необходимо подготовится к новой атаке. Спасибо за интересный разговор.