Презентация "Прямоугольный треугольник" (7 класс) по математике – проект, доклад
Презентацию на тему "Прямоугольный треугольник" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
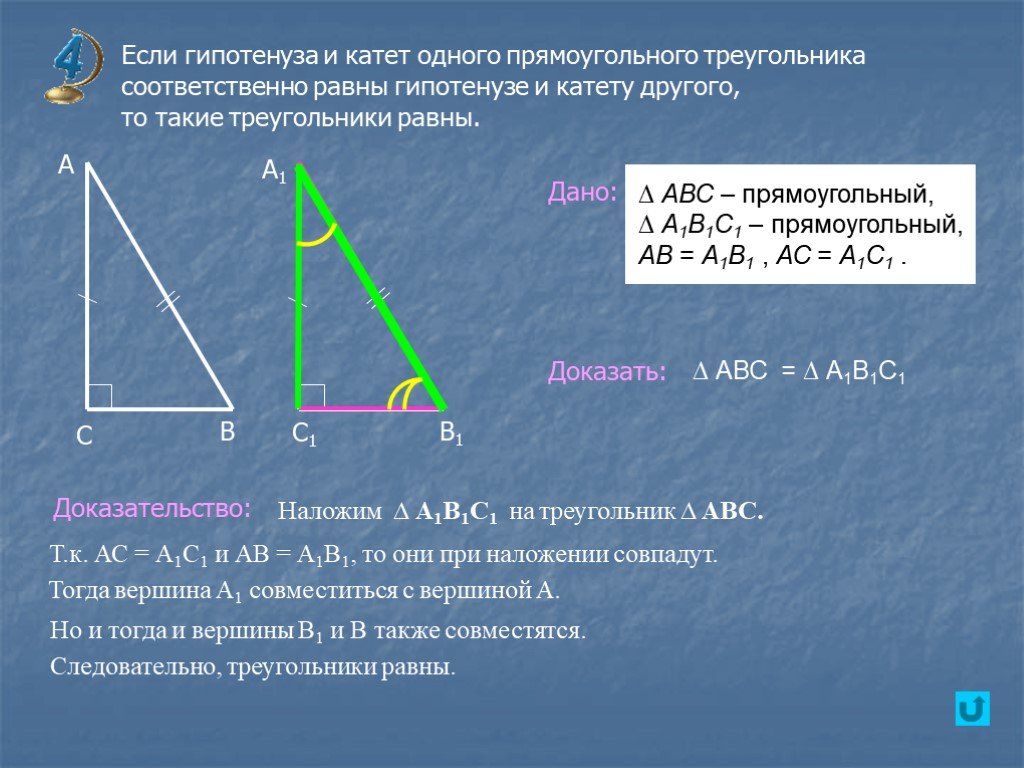
Прямоугольный треугольник
08.08.2019. Дроздова Татьяна Викторовна. Этапы урока. Организационный этап Сообщение темы изучение нового материала Закрепление новых знаний Ответы ...Прямоугольный треугольник
Цели урока:. Закрепить основные свойства прямоугольных треугольников. Рассмотреть признак прямоугольного треугольника и свойство медианы прямоугольного ...Прямоугольный треугольник и его свойства
Загадка. Три вершины тут видны, Три угла, три стороны,- Ну, пожалуй, и довольно! Что мы видим? Прямоугольный треугольник и его свойства. Викторина ...Прямоугольный треугольник
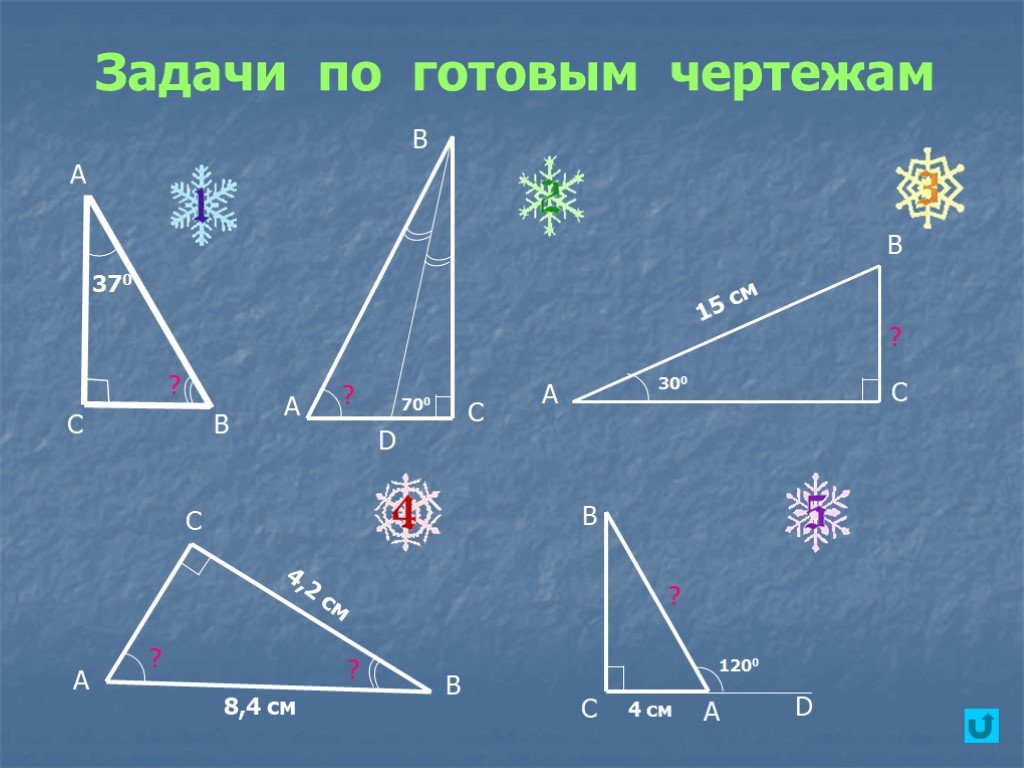
Прямоугольный треугольник. Тема урока:. Этапы урока. 1. Повторение пройденного материала 2. Решение задач 3. Самостоятельная работа 4. Подведение ...Прямоугольный треугольник - готовая презентация, для решения на готовых чертежах.
8 9 10 11 14 15 16 17 18 30 1 3 4 5 6 13 19 7. Найти: Дано: А C B. 2. D С 350. В β. 1500. 20 ? L 150. 1200. A b. . K H. 300. 12. α. . M N 450. E P. ...Прямоугольный треугольник в древнем Египте и в современной геометрии
Цель: познакомиться с историей применения прямоугольного треугольника в древнем Египте и на уроках геометрии. Групповая работа:. Землемеры Египетские ...Прямоугольный треугольник
1 ВАРИАНТ По горизонтали: б) Чему равен квадрат катета прямоугольного треугольника с гипотенузой, равной 13 см и другим катетом, равным 5 см. г) В ...Прямоугольный треугольник
Цели урока. Уметь определять по чертежам и словесным данным элементы прямоугольного треугольника. Применять свойства и признаки прямоугольных треугольников ...Прямоугольный треугольник, его свойства
Цели урока:. обучающая – знать свойства прямоугольного треугольника, уметь доказывать их, применять эти свойства при решении задач; развивающая – ...Прямоугольный треуголиник: синус, косинус, тангенс угла
C B A. Назвать катет, прилежащий к углу А. Назвать катет, прилежащий к углу В. Назвать катет, противолежащий углу А. Назвать катет, противолежащий ...Прямоугольный параллелепипед
Цель урока:. -познакомиться с прямоугольным параллелепипедом, кубом, их элементами; -научиться чертить эти фигуры; - находить длину ребёр и S поверхности. ...Равнобедренный треугольник
Цель урока:. ввести определение равнобедренного треугольника и его элементов; познакомится со свойством углов равнобедренного треугольника; научиться ...Равнобедренный треугольник
Цели:. Будь внимательней, дружок. Начинаем мы урок. Посмотрите, все ль в порядке: Книжка, ручка и тетрадка. Все ли правильно сидят? Все ль внимательно ...Прямоугольный параллелепипед. Куб
А В С D А1 В1 С1 D1. Прямоугольный параллелепипед, куб. К Х У Х1 У1 К1. Х,Х1 – вершины (8) ХК,КК1- рёбра (12) ХХ1К1К, ХХ1У1-грани (6). a b c V= abc ...Прямоугольный пареллелепипед.Куб
Что такое прямоугольный параллелепипед? Прямоугольный параллелепипед – это многогранник, составленный из шести прямоугольников. ____ видимая линия ...Прямоугольный параллелепипед и его свойства
Прямоугольный параллелепипед. Цель урока:. познакомиться с понятием прямоугольный параллелепипед, его составными частями, их свойствами, нахождением ...Прямоугольный параллелепипед
Прямоугольный параллелепипед - это тело, все грани которого - прямоугольники. Параллелос в переводе с древнегреческого буквально означает «идущие ...Прямоугольный параллелепипед
Параллелепипед. Параллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет 8 вершин и 12 рёбер. Грани параллелепипеда, ...Прямоугольный параллелепипед
Примеры предметов, имеющих форму прямоугольного параллелепипеда. Аквариум имеет форму прямоугольного параллелепипеда. Его боковые стенки – стеклянные. ...Прямоугольный параллелепипед
. . Решите задания и заполните таблицу. Найдите площадь квадрата, сторона которого равна 9 см. (П) Найдите площадь прямоугольника со сторонами 6 см ...Конспекты
Прямоугольный треугольник
Тема урока. : Прямоугольный треугольник. Цели урока. :. Образовательные. :. - создать условия для формирования у детей представления о прямоугольном ...Прямоугольный треугольник и его свойства
. . Учитель математики. МОУСОШ пгт Кумёны. Кумёнского района Кировской области. . Шехирева. . Наталья Валентиновна. Модель урока ...Прямоугольный параллелепипед и куб. Куб числа
Математика 3 класс. Тема: «Прямоугольный параллелепипед и куб. Куб числа". Цели: 1. Дать представление о прямоугольном параллелепипеде и кубе, ...Прямоугольный параллелепипед. Объем прямоугольного параллелепипеда
Технологическая карта урока. Разработчик. : учитель математики ГБОУ СОШ с. Криволучье-Ивановка. Самарской обл., Красноармейского р-она Баранов ...Прямой и развернутый углы. Чертежный треугольник
Тема: «Прямой и развернутый углы. Чертежный треугольник». Цели. : сформировать понятие развернутого угла, научить формулировать определение прямого ...Прямоугольный параллелепипед
Тема урока:. «Прямоугольный параллелепипед». . . Цели:. . ввести понятие прямоугольного параллелепипеда; показать правила изображения в тетради ...Прямоугольный параллелепипед
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №2 г.Турана. Разработка ...Равнобедренный треугольник и его свойства
Тема:. «Равнобедренный треугольник и его свойства». Цели урока:. Образовательные:. - обобщить и углубить знания по теме: «Свойства равнобедренного ...Прямоугольный параллелепипед
Конспект урока математики в 5 классе на тему «Прямоугольный параллелепипед». Цели урока. обучающая. : обучение нахождению объёма прямоугольного ...Прямоугольный параллелепипед
Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательная школа № 3 г. Козьмодемьянска». . Республики Марий Эл. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 мая 2019
Категория:Математика
Автор презентации:Кулешова Г.Н.
Классы:
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию