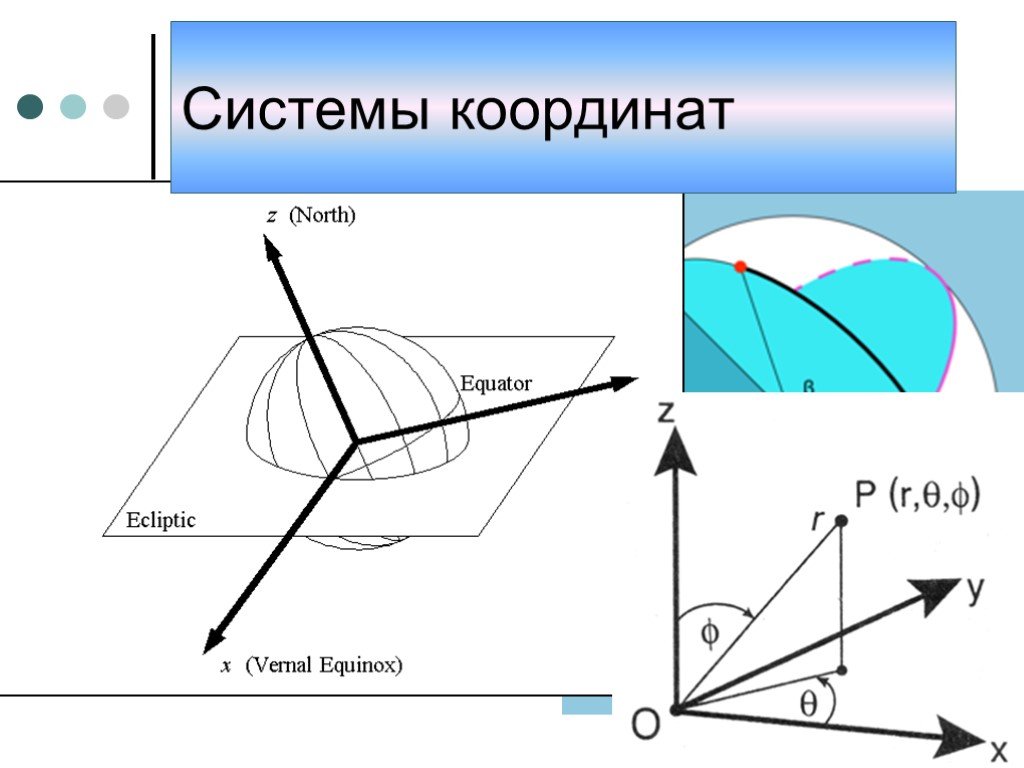
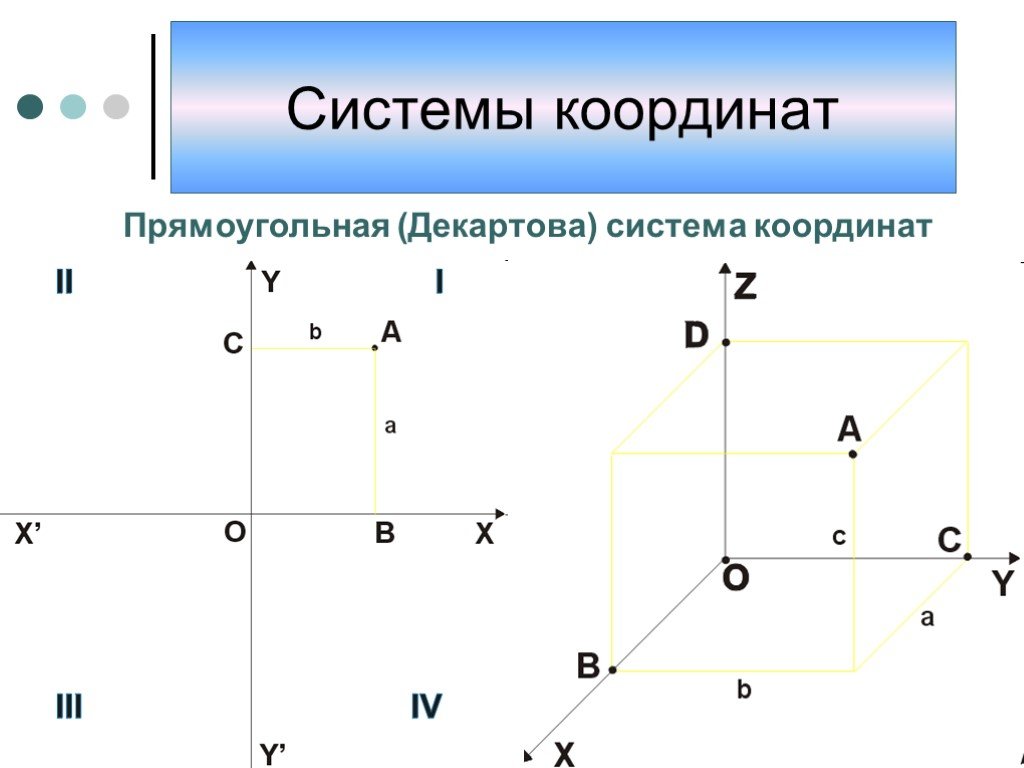
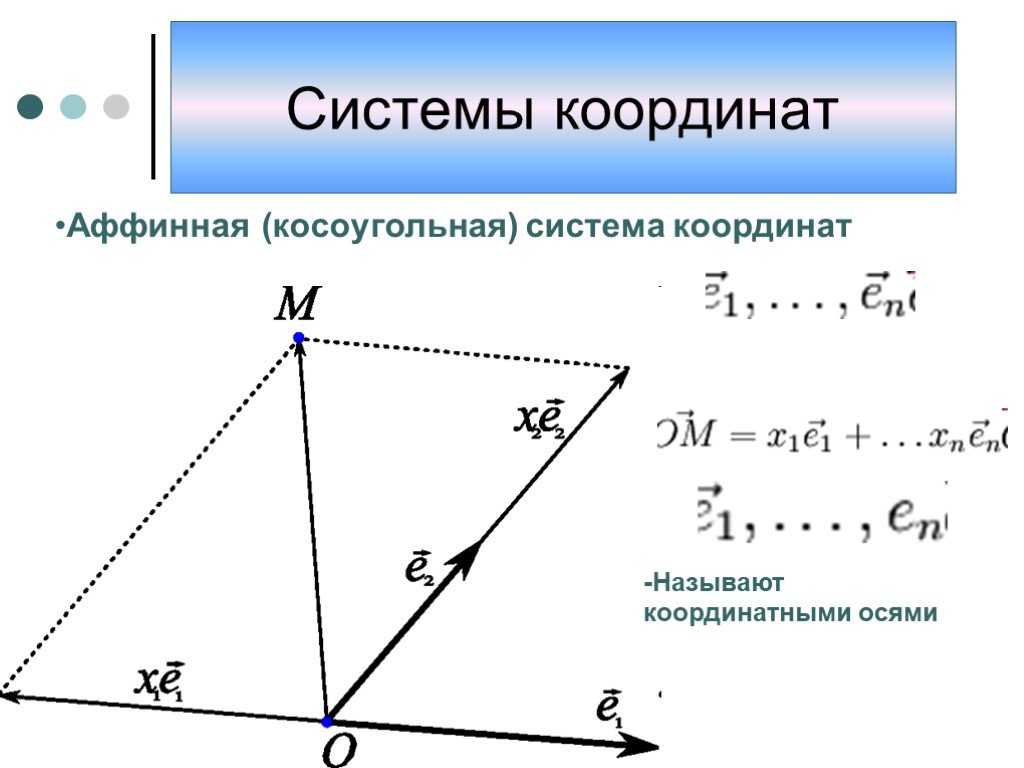
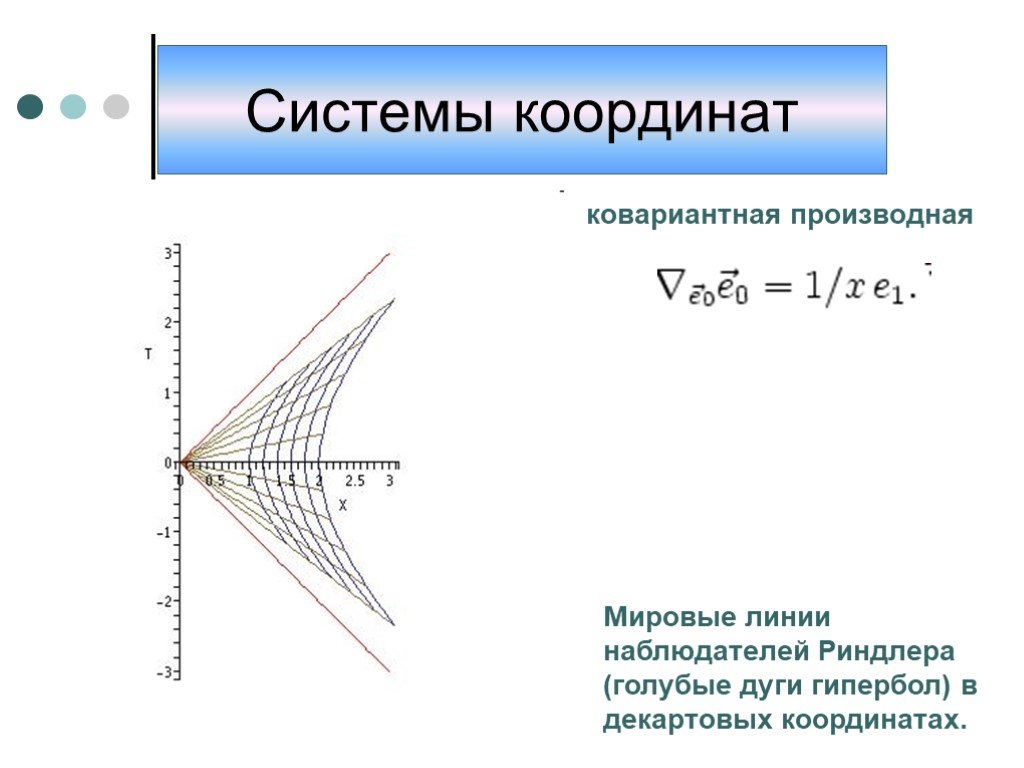
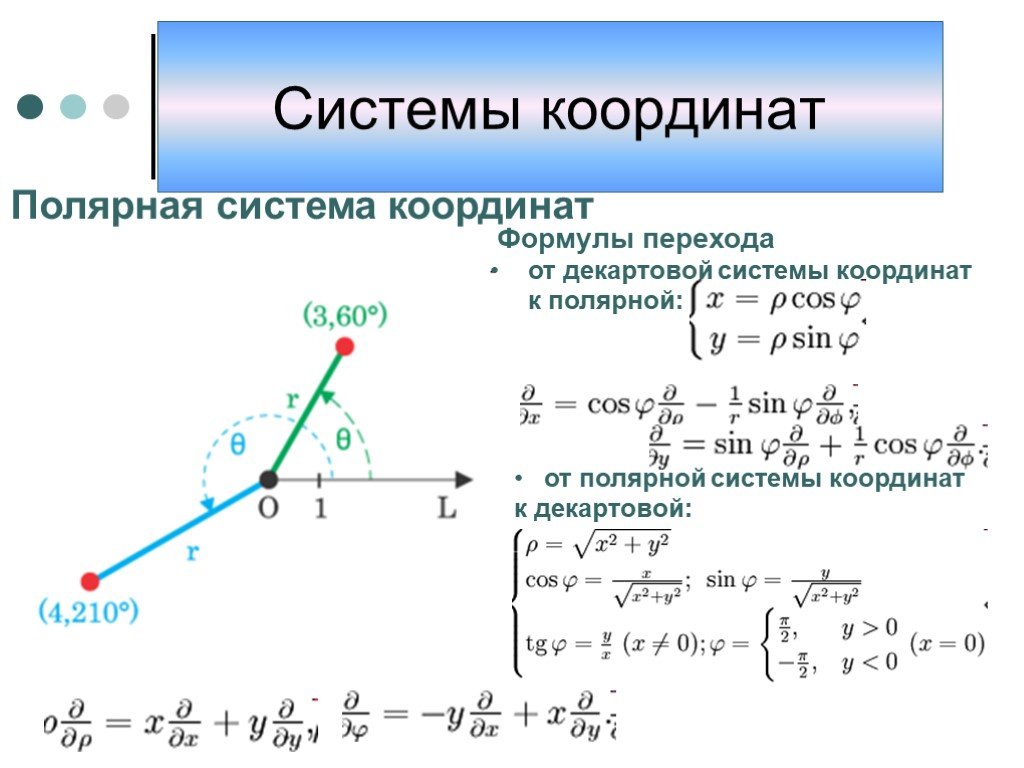
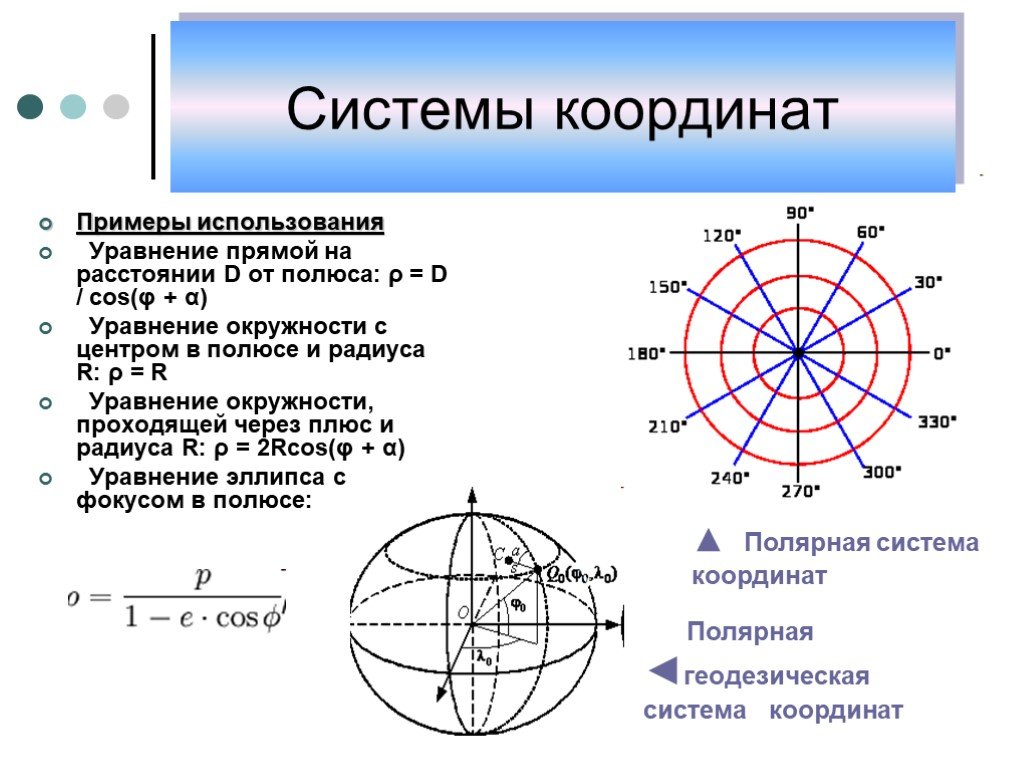
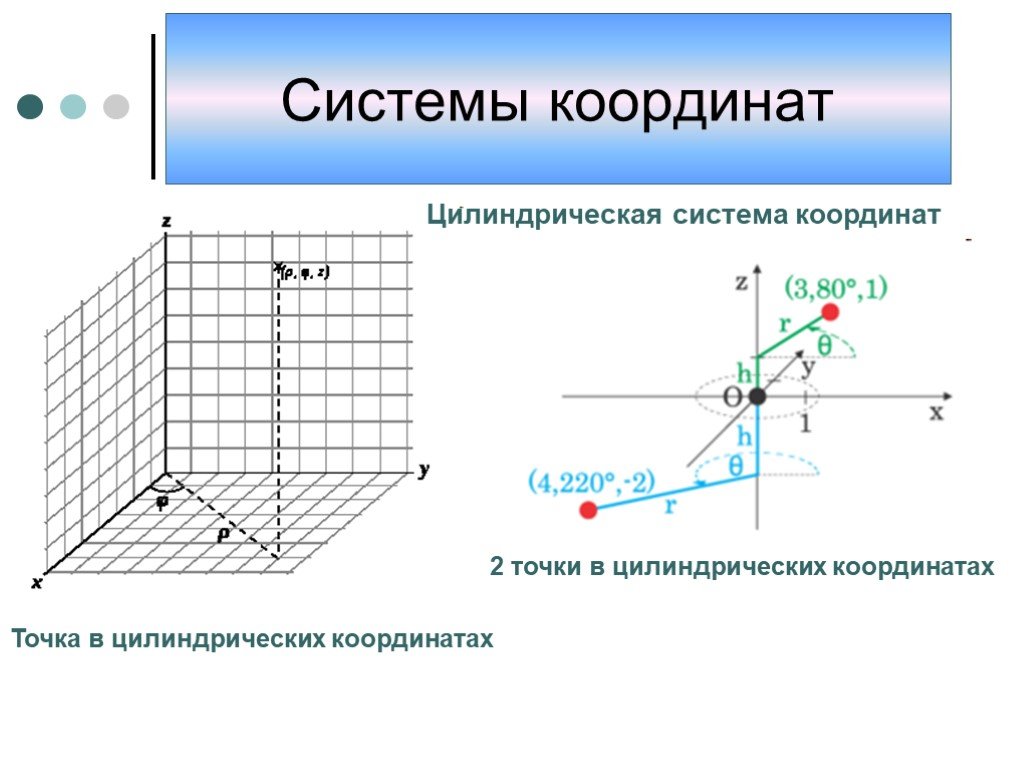
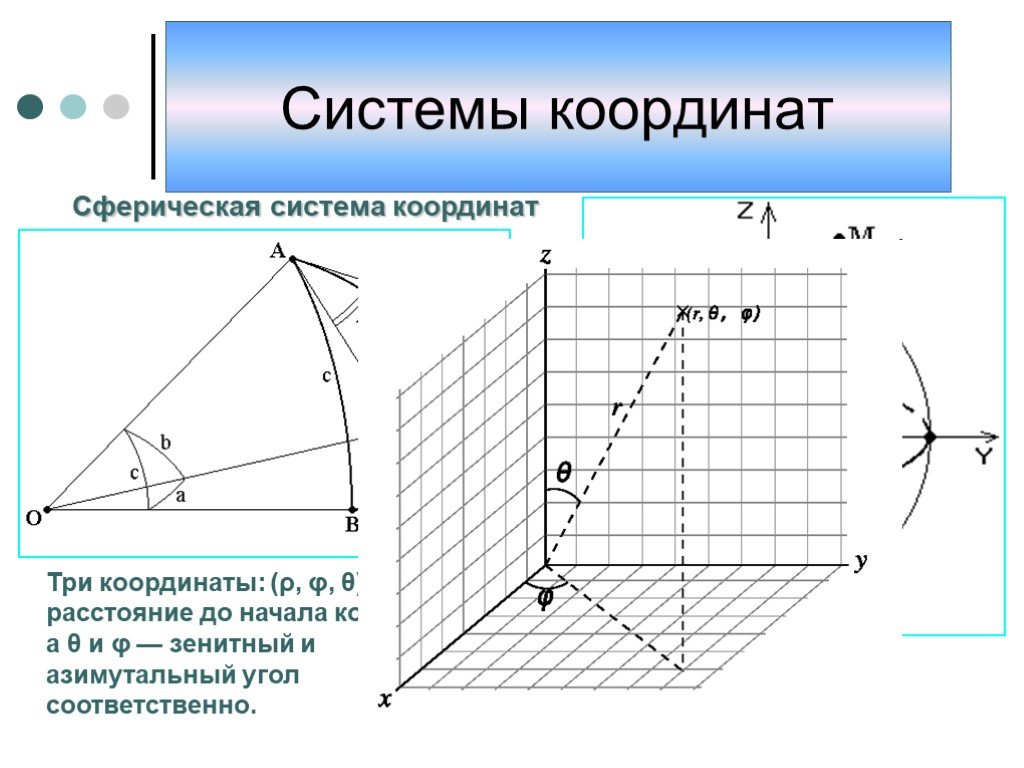
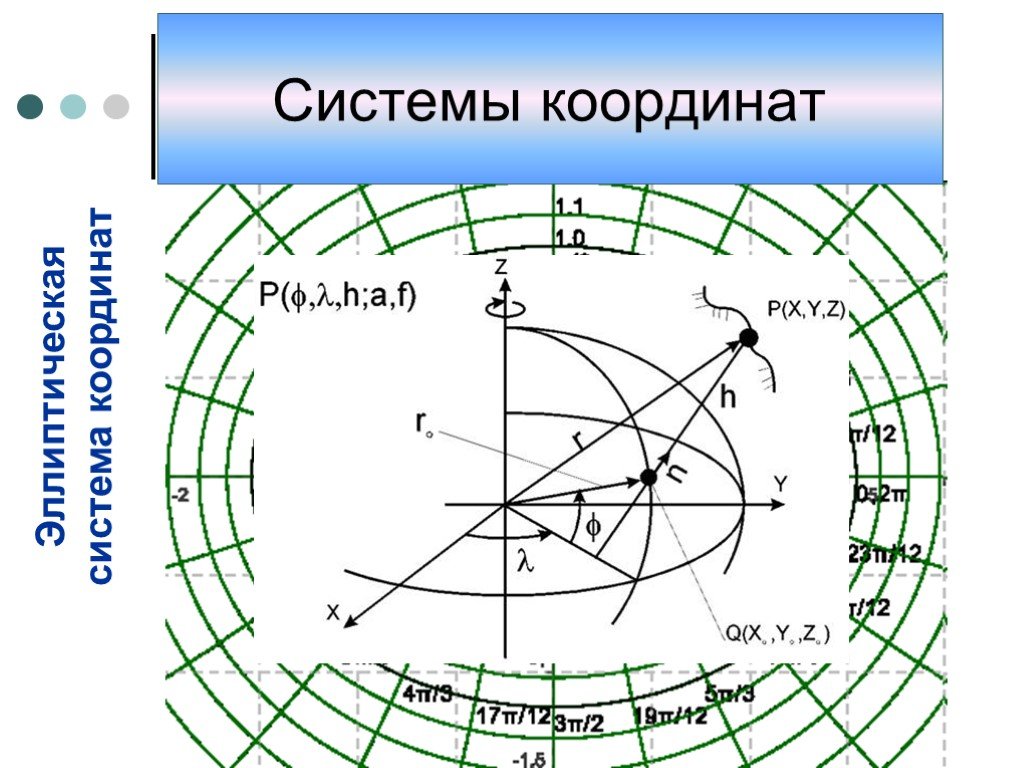
Презентация "Системы координат" по математике – проект, доклад

Презентация по геометрии

На тему: Системы координат

Выполнила: Лазарева Юлия, 11 Б класс

Системы координат

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющий положение конкретной точки, называется координатами этой точки. В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

Различные примеры систем координат

Прямоугольная (Декартова) система координат Аффинная (косоугольная) система координат Координаты Риндлера — в пространстве Минковского Барицентрические координаты Биангулярные координаты Полярная система координат Цилиндрическая система координат Сферическая система координат Тороидальная система координат Параболическая система координат Параболоидальные координаты Бицентрические координаты Биполярные координаты Бицилиндрические координаты Биангулярные координаты Трилинейные координаты Проективные координаты Эллипсоидальные координаты (эллиптические координаты) Конические координаты

Прямоугольная (Декартова) система координат

Аффинная (косоугольная) система координат

-Называют координатными осями

Координаты Риндлера

Связь с декартовыми координатами Для получения координат Риндлера естественно начать с галилеевых координат В области , которая часто называется Клином Риндлера, определим новые координаты, через следующее преобразование Обратным преобразованием будет В координатах Риндлера линейный элемент пространства Минковского переходит в

Мировые линии наблюдателей Риндлера (голубые дуги гипербол) в декартовых координатах.

ковариантная производная

Полярная система координат

Формулы перехода от декартовой системы координат к полярной:

от полярной системы координат к декартовой:

Примеры использования Уравнение прямой на расстоянии D от полюса: ρ = D / cos(φ + α) Уравнение окружности с центром в полюсе и радиуса R: ρ = R Уравнение окружности, проходящей через плюс и радиуса R: ρ = 2Rcos(φ + α) Уравнение эллипса с фокусом в полюсе:

▲ Полярная система координат

Полярная ◄геодезическая система координат

Цилиндрическая система координат

Точка в цилиндрических координатах

2 точки в цилиндрических координатах

Сферическая система координат

Три координаты: (ρ, φ, θ), где ρ — расстояние до начала координат, а θ и φ — зенитный и азимутальный угол соответственно.

Эллиптическая система координат

Спасибо за внимание!