Конспект урока «Системы уравнений с двумя переменными » по алгебре для 9 класса
Аттестуемый педагог (ФИО) Толмачева Галина Николаевна
Предмет: алгебра
Класс: 9 Б
Тема урока: Системы уравнений с двумя переменными.
Цель урока:
Расширить представление обучающихся о системах уравнений с двумя переменными и способах их решения; рассмотреть графический метод решения систем уравнений.
Задачи:
-
- Обучающие – сформировать умение графически решать системы уравнений с двумя переменными ; повторить графики функций, дать наглядные представления о возможном количестве решений систем уравнений.
-
- Развивающие – развивать у учащихся мыслительную деятельность; самостоятельность; аккуратность при построении графиков, логическое мышление (вывод, анализ, обобщение).
-
- Воспитательные – формировать интерес к предмету; графическую культуру; уважение чужого мнения; дисциплинированность.
Тип урока: урок изучения нового материала.
Формы работы учащихся: индивидуальная, фронтальная, с использованием ИКТ
Оборудование: проектор, экран, презентация, таблички с функциями, плакат с графиками систем уравнений, макет окружности.
Ход урока
| Цель | Деятельность учителя | Деятельность учащихся | ||||||||||||||||||||
| 1. Орг. момент | Организовать работу обучающихся на уроке, настроить обучающихся на учебную деятельность, предмет и тему урока. | В начале урока построение, приветствие ребят и учителя. Сообщение темы урока. - Здравствуйте ребята, сегодня на уроке мы будем изучать тему: Системы уравнений с двумя переменными ( слайд №1) | | |||||||||||||||||||
| 2.Повторение | Повторить учебный материал, встречающийся при изучении новой темы. | - Ребята, посмотрите на слова, из которых состоит тема нашего урока. - В название темы встретились ли вам знакомые слова? - Какие? - Что же такое уравнение? - А какие виды уравнений вы знаете? - А что значит решить уравнение? - Сколько переменных в этих уравнениях? - А в названии нашей темы, сколько должно быть переменных? Назовите пример линейного уравнения с двумя переменными. - Можно ли выразить из этого уравнения одну переменную через другую? - А какую переменную вы хотите выразить? Давайте, ее выразим А другую переменную можно выразить? Выразите ее - Что вам напоминает выражение с переменной у? - А как называется эта функция? -Как можно ее увидеть?
- А теперь усложним это уравнение. - Какое уравнение получится? - Знакомо вам это уравнение? - Что является графиком квадратичной функции? - Из какой функции получена данная функция? С помощью какого преобразования?
Так как мы заговорили о функциях, вспомните, какие еще бывают функции, и поздороваемся с ними. - Вы же здороваетесь со знакомыми людьми? Вот и мы будем здороваться со знакомыми функциями и рассказывать о них все, что знаем. (учитель показывает таблички с различными видами функций, а ученики определяют их название и график)
-Хорошо, молодцы, справились с заданием, а теперь давайте вспомним, как выглядят графики функций. Слайд 2) - Как называется каждая из функций? - Задания с графиками очень часто встречаются на ГИА по математике. Рассмотрим одно из таких заданий. Соотнесите график функции с соответствующей формулой.( Слайд 3) - Мы повторили все, что связано со словами « уравнение с двумя переменными» , а теперь вернемся к теме урока - Какое же слово мы не разобрали? - Что же значит слово « система»? - Давайте посмотрим, что означает слово система по толковому словарю. -Но ведь с этим словом мы с вами уже знакомы, и в 7 и 8 классах мы решали системы уравнений. - А, что значит решить систему уравнений? - Какими способами можно решить систему уравнений? - Сегодня мы будем рассматривать только графический способ. -А теперь сформулируйте цель нашего урока. | Да Уравнения Это равенство, содержащее буквы Линейные, квадратичные, дробные, целые Найти неизвестную переменную Одна Две х +у = 5 Можно х х =5 – у Да у = 5 - х Функцию Линейная Построить график прямой, для его построения достаточно взять две точки. у = 5- Да, это уравнение квадратичной функции Парабола, ветви направлены вниз Из функции у= - Да Это прямая пропорциональность, графиком является прямая, проходящая через начало координат. Если к>о, то график располагается в 1 и 3 координатной четверти, если к Это обратная пропорциональность, графиком является гипербола. Если к>о, то график располагается в 1 и 3 координатной четверти, если к Это уравнение окружности с центром в точке ( Линейная, обратная пропорциональность, прямая пропорциональность, квадратичная, линейная На рисунке А изображена прямая проходящая через начало координат, она является графиком прямой пропорциональности отмеченной под цифрой 1. На рисунке Б изображена гипербола- график обратной пропорциональности, он отмечен под цифрой 2. Под буквой В изображена парабола- график квадратичной функции ей соответствует номер 3. Система Дети высказывают свое мнение Система- форма организации чего- нибудь, нечто целое, представляющее единство взаимосвязанных частей Да Найти все решения или установить, что их нет Подстановки, сложения Дети формулируют цель урока: Сегодня мы должны рассмотреть системы уравнений и научится их решать графическим способом. | |||||||||||||||||||
| 3. Объяснение нового материала | Рассмотреть графический способ решения систем уравнений с двумя переменными Вывести алгоритм графического способа решения систем уравнений с двумя переменными | Давайте откроем тетради, запишем в них число, тему урока. - Для того чтобы определить как же решается система уравнений графическим способом разберем пример ( Слайд 4) -Можем ли мы сразу найти решение этой системы уравнений графическим способом? - А как же нам поступить? -Чем представлено первое уравнение? - Чем является график второго уравнения? -Куда направлены ветви параболы? Почему? - Что происходит с графиками этих уравнений? -Сколько точек пересечения мы видим? -Назовите координаты каждой точки. -Сформулируем алгоритм решения систем уравнений графическим способом. Молодцы, хорошо. -Давайте проверим по слайду, верно ли мы составили алгоритм графического способа решения систем уравнений. ( Слайд 5) -Прочитайте его - Самый лучший результат для запоминания возникает, когда работает комбинированная память. Мы можем видеть о чем говорим, про себя проговаривать и записывать . Запишите алгоритм себе в тетрадь и про себя проговорите его. - При решении системы уравнений мы видели, что графики пересекались в четырех точках - Как вы думаете, могут ли эти графики иметь другое расположение? - Когда это возможно? - Сколько же может быть точек пересечения, если мы будем двигать окружность? - Сколько решений при этом может иметь система уравнений? - От чего зависят решения? | Дети записывают в тетрадях число, классная работа, тема урока. Нет В одну систему координат поместить оба графика Окружностью с центром в начале координат и радиусом равным 5 Параболой с вершиной в точке(1;6) Вниз Так как перед Пересекаются 4 А(-2; -4,5), В(0; 5), С(2,5; 4,2); D(4;-3). Дети пытаются вывести алгоритм графического способа решения систем уравнений.
1 человек читает алгоритм Со слайда переписывают алгоритм Да Если сдвинуть окружность 3,2,1, не иметь общих точек 1, 3 ,2,несколько, не иметь решений От количества общих точек | |||||||||||||||||||
| 4.Музыкальная пауза | Мы с вами хорошо поработали, а теперь немного отдохнем, послушаем хорошую музыку и представим, что мы на берегу океана, вокруг нас шумят волны, ярко светит солнце. | | ||||||||||||||||||||
| 5.Формирование умений и навыков | Закрепить полученные знания с помощью тренировочных заданий и упражнений. Проконтролировать степень усвоения нового учебного материала | -Отдохнули, а теперь поучимся составлять уравнения и определять количество решений в системах. выполним №441 Прочитайте задание. -Что нужно сделать в этом задании? - Назовите первую систему? - Сколько решений имеет эта система? Почему? - Назовите вторую систему? - Сколько решений имеет вторая система? Почему? - Назовите третью систему? - Сколько уравнений должно быть в системе уравнений? -А у нас сколько? -Что же вы можете об этом сказать? - Как же будет выглядеть система? - Сколько решений она будет иметь? Почему? - Теперь постараемся составить систему уравнений по имеющимся графикам. Выполним№443 а ( на доске закреплен плакат с графиками данных систем уравнений). -Запишите получившуюся систему - Что мы уже научились делать? - А теперь вспомним, как записываются решения систем уравнений ( Слайд 6) - Что значить решить эту систему? -Как найти координаты точек пересечения? - У первой точки, какие координаты? - Назовите координаты второй точки - Какой ответ у вас получился? - Мы составляли системы уравнений, определяли количество корней в системе, а теперь перейдем к решению системы уравнений графическим способом х-у=0 х∙у=4
- Чем будем пользоваться при решении системы? - Что нужно сделать сначала? Что получилось? - Что вы можете сказать о первом уравнении системы? - Сколько точек нужно для ее построения? - Что вы можете сказать о втором уравнении системы? - Что является графиком этой функции? - Какие значения х можно брать для составления таблицы значений функции? -- Что нам нужно дальше выполнить? -А потом? - Сколько решений имеет данная система? - Назовите решения системы уравнений? | Записать систему уравнений и определить количество решений для каждой из систем уравнений
у- х=3 у+2х= -3 1 решение, так как графики пересекаются в 1 точке
2у-х=-4 Не имеет решений, так как графики не пересекаются Могут возникнуть затруднения 2 1 Уравнения совпадают
у+2х=4 у+2х=4 Бесконечно, так как системы уравнений совпадают 2
у+2х=2 Составлять системы уравнений и определять количество решений этих систем Нужно найти координаты точек пересечения двух уравнений Опустить перпендикуляры на оси х и у из каждой точки (-2;5) (2;- 3) (-2;5); (2;- 3) ( 1 человек решает у доски, остальные в тетради) алгоритмом Из каждого уравнения системы нужно выразить переменную у через х
у= Это уравнение прямой пропорциональности, графиком является прямая, проходящая через начало координат достаточно взять 1 точку Составим таблицу
Это уравнение обратной пропорциональности Гипербола Любые , кроме 0 Составим таблицу
Построить уравнения в одной системе координат Найти координаты точек пересечения этих уравнений 2 (-2;-2); (2;2) | |||||||||||||||||||
| 6. Итог | Систематизировать информацию, полученную на уроке | Мы очень хорошо поработали, подведем итог нашей работы. - Чем мы сегодня занимались? - Так что же такое система уравнений? - Что называют решением системы уравнений с двумя переменными? -В каком случае система имеет единственное решение? -В каком случае система имеет бесконечное множество решений? -Когда система не имеет решений? -Сформулируйте алгоритм графического решения систем уравнений | Графически решали системы уравнений Системой уравнений называют некоторое количество уравнений, объединенных фигурной скобкой. Пару значений переменных х и у , обращающих каждое уравнение в верное равенство. Когда два уравнения имеют 1 точку пересечения графиков Когда два уравнения совпадают Когда два уравнения не имеют общих точек Дети формулируют алгоритм графического решения систем уравнений по памяти. | |||||||||||||||||||
| П.3.5 №442(а; в), №444 б Наш урок мне бы хотелось закончить строчками. Приобретать знания - храбрость Приумножать их - мудрость А умело применять- великое искусство! И вы действительно храбро искали пути решения системы с двумя переменными графическим способом. Мудро составляли алгоритм графического способа решения с двумя переменными, и умело применяли свои знания. Учитель благодарит учеников за урок | Дети записывают домашнее задание в дневники | ||||||||||||||||||||
Учитель__________________________________________ Толмачева Галина Николаевна
Здесь представлен конспект к уроку на тему «Системы уравнений с двумя переменными », который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.


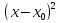 +
+ =
=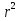 Что вы можете сказать об этом уравнении?
Что вы можете сказать об этом уравнении?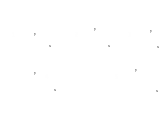

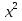
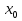 ;
;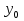 ) и радиусом
) и радиусом 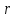 .
.

 - На каком рисунке система уравнений имеет два решения?
- На каком рисунке система уравнений имеет два решения?
 - Запишите №444 (а)
- Запишите №444 (а) 
 2у-х=6
2у-х=6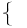
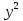 =4
=4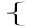 у=х
у=х