Презентация "Старинные задачи" по математике – проект, доклад
Презентацию на тему "Старинные задачи" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Понятие задачи
О чем будет урок ? Задание 1. Правильный ответ А. Продолжаем размышлять… Задание 2. 1 ? 4. Задание 3 5. часть Думаем и отвечаем. . целое +. 4 + 1 ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Основные задачи на проценты
Представьте данные десятичные дроби в процентах:. 0,5=…% 123=…% 0,045=…% 0,6=…%. 0,0035=…% 0,123=…% 70,5=…% 0,01=…%. 10=…% 1,5=…% 7,2=…% 0,42=…%. ...Площадь треугольника. Полезные теоремы, следствия и задачи
Вспомните ответы на вопросы. 1) Сформулируй понятие площади геометрической фигуры. 2) Сформулируй основные свойства площадей геометрических фигур. ...Логические задачи на переправу без чисел
Цель: собрать материал о логических играх без чисел, систематизировать и представить материал для работы в школьных математических кружках. Задачи. ...Нестандартные задачи для шестиклассников
1 4 5 6 7 3. Продолжите ряд чисел: 10, 8, 11, 9, 12, 10, … до восьмого числа. По какому правилу он составлен? ответ. Найти площадь треугольника. Площадь ...Взаимообратные задачи
Условие Вопрос Схема Выражение Решение Ответ. На кормушке сидело 2 синички. Прилетела ещё 1синичка. Сколько синичек прилетело? На кормушке сидело ...Логические задачи
Задача «Школьные учителя». В старших классах работают три учителя: Воронов, Соколов и Коршунов. Каждый из них преподает по два предмета, так что в ...Вводные задачи
Задачи на чередование. 1.На плоскости располо- жено 11 шестеренок,со- единенных по цепочке. Могут ли все шестеренки вращаться одновременно? Ответ:нет.Если ...Великие задачи математики. Квадратура круга
Автор: Монахов Станислав. МОУ "Средняя общеобразовательная школа № 59". Курск - 2006. Меня зовут Монахов Станислав. Я ученик 6-го класса, очень люблю ...Введение понятия "Задачи. Составные части задачи
4. 10. . . 3. Проверьте! 4 10 5 6 3 3 4 5 6 10. Что отсутствует у нашего солнышка, а в математике учит считать? Учит луч! 1 2 5 6 7 8 9 0+1 1+1 2+1 ...Анания Ширакаци и его задачи
Дата рождения: около 610 год Место рождения: в области Ширак провинции Айрарат Дата смерти: около 685 год Научная сфера: математик, астроном, географ. ...Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). ...Комбинаторные задачи и их решения
1) Цели и задачи 2) Пояснительная записка 3) Требования к уровню подготовки 4) Учебно– тематический план 5) Содержание программы 6) Поурочное планирование ...Геометрические задачи «С2»
«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. ...Логические задачи
Пётр - сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору? задача 1 внуком сыном дедом. 2 4 6. Уменьшаемое больше вычитаемого на 2. Чему ...Геометрические задачи на построение
Задачи на построение. Окружность Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже ...Логические задачи для детей
В магазине было шесть разных ящиков с гвоздями. Масса ящиков в 6, 7, 8, 9, 10 ,11 кг. Два покупателя приобрели пять ящиков, причём каждому гвоздей ...Геометрические задачи на экстремум
Определения. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть ...Наши задачи
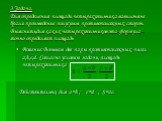
На ярмарке браслет из драгоценных камней стоимостью 67рублей 35копеек. Переведите их в старинные меры денежных единиц. Как вы знаете, что каждый уважающий ...Конспекты
Простые и составные задачи
Тема урока:. Простые и составные задачи. Цель: знакомство с понятиями простая и составная задача, выявление существенных признаков этих понятий. ...Упражнения и задачи на усвоение таблицы деления на 2. Закрепление
Урок математики во 2 классе. Тема: Упражнения и задачи на усвоение таблицы деления на 2. Закрепление . . Урок - закрепление. Цели:. -Воспроизводить ...Взаимно обратные задачи
Математика. Тема:. Взаимно обратные задачи. Цель:. Сформировать представление о взаимно обратных задачах, умение их распознавать и составлять задачи ...Старинные единицы измерения длины
. Проектная работа. «Старинные единицы. . измерения длины». Выполнил: Осипов Владислав,. . ученик 5 класса ГБОУ ...Старинные русские меры длины
Разработка внеклассного мероприятия по теме: «Старинные русские меры длины». Автор. :. Ахметшина Р. М., учитель математики, г. Набережные Челны. ...Решаем задачи
Математика: «. Решаем задачи». Цели. :. закрепление навыков решения задач в 1 действие на сложение и вычитание. Задачи:. . Обобщить полученные ...Решение задачи исследовательского характера
Лукашова Маргарита Александровна, учитель математики МБОУ г. Мурманска лицей №4. . Предмет: математика. Возраст детей: 7 класс. Место проведения: ...Задача. Структура задачи
Технологическая карта урока математики в 1 классе. . МБОУ СОШ №174. Учитель:. Павлова Елена Валерьевна. Дата проведения:. 18 марта 2014г. ...Задача. Структура задачи
. . . Учитель начальных классов Белослудцева Ирина Леонидовна. . Предмет:. . Математика. Класс:. 1 класс. Тип урока:. . ОНЗ. Тема:. ...Девять решений геометрической задачи
Муниципальное бюджетное общеобразовательное учреждение. «Верхнеуслонская средняя общеобразовательная школа». Верхнеуслонского муниципального района ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 февраля 2019
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию